Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Theoretical Framework
Unlock Audio Lesson
Today, we are going to explore some fundamental concepts in fluid dynamics! Let's start with a basic question. What happens to the velocity and pressure when the flow is steady?
I think the velocity and pressure remain constant over time?
Exactly! In steady flows, these parameters don't change. Now, does anyone know what a streamline is?
Isn't it a line that represents the direction of fluid flow?
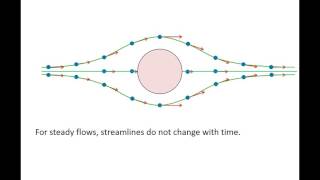
Yes, good job! A streamline is a line tangent to the velocity vector at any point in the flow field. They help us visualize the flow direction.
Understanding Streamlines
Unlock Audio Lesson
Let's dive deeper into streamlines. Can anyone recall how they are defined?
A streamline is a path along which a fluid flows; there’s no flow across it.
Right again! And one interesting fact is that in a steady flow, streamlines, pathlines, and streaklines will all coincide. Can you explain why that is?
Because the flow parameters don’t change with time, right?
Perfect! The consistency in conditions leads to this alignment, which simplifies our analysis.
Pathlines and Streaklines
Unlock Audio Lesson
Now, moving on to pathlines—who can explain what they represent?
Pathlines show the trajectory of fluid particles over time.
Exactly! Whereas streaklines show all particles that have previously passed a prescribed point. Can anyone provide an example of how we visualize these?
Like adding dye in the flow to see where the fluid has been?
Yes! By releasing dye in a flow, you can see streaklines. It's a practical application!
Applications of Fluid Lines
Unlock Audio Lesson
Let’s talk about where we use these concepts, such as in predicting weather patterns or analyzing flow around structures. Why do you think understanding these lines is important in real-life applications?
Maybe it helps us design better buildings or airplanes.
Exactly! Engineers use this understanding to make informed designs to handle forces acting on structures. Can anyone name a situation where this knowledge is critical?
Like in aerospace engineering, to ensure the aircraft can withstand forces from the air?
Spot on! This knowledge is essential in many fields, not just engineering.
Review and Summary
Unlock Audio Lesson
To summarize, today we discussed streamlines, pathlines, and streaklines—how they define different aspects of fluid motion. Can anyone recall the main difference between these three terms?
Streamlines show flow direction, pathlines show individual particle movement, and streaklines indicate where particles passed a point!
Well summarized! Remember these concepts as they are vital for understanding fluid dynamics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the concepts of pathlines, streamlines, and streaklines are defined and differentiated, illustrating how these terms represent different perspectives on fluid motion. The teacher emphasizes their significance in understanding fluid dynamics and illustrates key points with examples, relating them to the pressure and velocity fields.
Detailed
Detailed Summary
In this section, we delve into the concepts of pathlines, streamlines, and streaklines which are essential in fluid dynamics. The discussion begins with a simple analytical approach to obtaining solutions for velocity, pressure distributions, and their compliance with conservation equations. The section emphasizes that in steady flow conditions, understanding the velocity and pressure fields is crucial.
Key Definitions and Concepts:
- Streamline: Defined as a line where every point is tangential to the velocity vector at a particular instant of time. Hence, it is useful in visualizing the flow direction at any point in a fluid.
- Pathline: Represents the actual path traversed by a fluid particle over time. It helps in following the motion of individual particles.
- Streakline: Describes the locus of all particles that have passed through a specific point in space over time, typically visualized with dyes in experimental setups.
These lines help gauge the behavior of fluids in various scenarios, such as wind flow over structures or jet impacts on surfaces, and their understanding is crucial for analyzing complex fluid flow problems effectively. Moreover, they all converge into the same representation in steady flows, creating a crucial insight into fluid mechanics. This understanding is generally supported with examples and potential applications, enhancing comprehension and visualization of fluid motion.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Velocity Fields
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So now I am just defining them the velocity field, when we are talking about we are talking this velocity as a vector quantity, which vary in a space in case of the Cartesian coordinate system of x, y, z and the time. But most often for easy point of view, we resolve this velocity vector component into its scalar component in Cartesian coordinate systems like the i and j and k.
Detailed Explanation
In fluid mechanics, the velocity field describes how the velocity of fluid changes in space and time. We treat velocity as a vector, which means it has both magnitude and direction. The components of this velocity vector can be broken down into three parts - u (x-direction), v (y-direction), and w (z-direction). This makes it easier to analyze complicated flows by isolating each directional component.
Examples & Analogies
Imagine you are flying a drone. The speed and direction the drone is moving can be broken down into movements along the ground (x and y directions) and height (z direction). By understanding these three components of the drone's motion, you can better control its flight path.
Defining the Velocity Field
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
V(x, y, z, t) = u(x, y, z, t) + v(x, y, z, t) + w(x, y, z, t)
Detailed Explanation
The velocity field can be expressed mathematically as a combination of its three components: V(x, y, z, t) represents the overall velocity at any point in space at a given time. It combines the x-component (u), y-component (v), and z-component (w), which are all functions of position and time. This formulation allows engineers to analyze how fluids behave under different conditions.
Examples & Analogies
Think about a river's flow. The total velocity of the river at any point can be thought of as the sum of how fast it moves in various directions - downstream (u), sideways (v), and possibly upward or downward based on obstacles and terrain (w).
Pressure in Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now as already I discussed that we talk about the pressures which is very dynamic variables, the pressure distribution play the major roles because as you know it the flow is come from high energy to the low energy.
Detailed Explanation
Pressure in fluid mechanics is crucial because it determines the behavior of the fluid flow. Fluids naturally flow from areas of high pressure (high energy) to areas of low pressure (low energy), so understanding pressure distribution helps to predict how fluids will move within a system. This forms the foundation for many fluid mechanics problems, especially when considering forces that drive fluid movement.
Examples & Analogies
Imagine draining a bathtub. Water flows out through the drain due to the difference in pressure (higher pressure in the water above), which pushes it down. Similarly, understanding how pressure works in other systems helps predict how fluids, like oil in pipelines or air in ducts, will behave.
Pathlines vs Streamlines vs Streaklines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
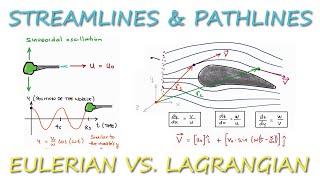
So if you look at that the streamline is a line everywhere it is a tangent to the velocity vector at given instant. The actual path traversed by a given fluid particle is called the pathline. The streakline is a locus of the particles that have earlier passed through a prescribed point.
Detailed Explanation
Streamlines, pathlines, and streaklines are different methods to visualize fluid flow. A streamline shows the direction of fluid flow at an instant - it is like taking a photograph of a flowing river at a specific moment. A pathline represents the trajectory taken by a specific fluid particle over time. A streakline is like a trail of dye through the fluid, showing where particles have flowed through an identified point. When flow is steady, all three types of lines coincide, providing an accurate depiction of the flow.
Examples & Analogies
Think of a river again. The streamlines are like the lines on a map showing the river's path at a specific time. If you dropped a colored dye from a bridge, the streakline would represent the way that dye spreads across the water. If you were to track a leaf floating down the river, the pathline would show where that leaf goes over time. In a steady river flow, the lines would show similar paths, reinforcing how the water moves.
Understanding Flow Visualization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So mostly in case of the analytical methods we follow the stream tube or streamlines methods more accurately, but the experimental technique when you visit either we follow for a technique like pathlines like we track a fluid particle at different instant of time...
Detailed Explanation
Analytical methods in fluid mechanics often focus on streamlines to solve problems since they represent the velocity vectors at a specific time effectively. However, when conducting experiments, it might be more practical to observe pathlines or streaklines—tracking where fluid particles go (pathlines) or marking where they've been (streaklines). These techniques help visualize and understand flow behavior, especially in complex scenarios.
Examples & Analogies
Consider a water slide. When someone goes down, you could visualize their path (pathline) through a camera. If you sprinkle colored powder on the water, you can see how it disperses (streakline). Both methods give you insights into how the water flows around the slide and others on it.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Streamline: A line that shows the direction of flow.
-
Pathline: Path traveled by a fluid particle over time.
-
Streakline: Locus of particles that passed a point.
-
Velocity and pressure fields: Important for analyzing fluid flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Visualizing water flow in a river can illustrate streamlines, as they show how the water travels around curves and obstacles.
-
Using colored dye injected into a water flow can help visualize streaklines and how fluid particles travel in time.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Streamlines show flow with no fears, Pathlines draw paths of water cheers, Streaklines mark spots with color bright, In fluid mechanics, they guide our sight.
📖 Fascinating Stories
-
In a colorful stream, a curious fish follows a red trail of dye. It wonders where all the other fish have been, tracing their streaklines while following the current, illustrating how pathlines differ from streaklines.
🧠 Other Memory Gems
-
Remember S.P.S: Streamlines show direction, Pathlines show passages, Streaklines follow spots.
🎯 Super Acronyms
SPP for Streamline, Pathline, and Streakline - understand how they differ to master fluid flows.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Streamline
Definition:
A line representing the direction of flow in a fluid, tangential to the velocity vector.
-
Term: Pathline
Definition:
The actual path followed by a fluid particle over time.
-
Term: Streakline
Definition:
The locus of all particles passing through a specific point over time.
-
Term: Velocity Field
Definition:
A vector field that represents the velocity of fluid particles at different points in space.
-
Term: Pressure Field
Definition:
A scalar field that represents the pressure at various locations in a fluid.