Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Velocity Fields
Unlock Audio Lesson
Let's begin with velocity fields. The velocity field represents how the velocity of a fluid varies in space and time. Can anyone tell me how we can express a velocity field in a Cartesian coordinate system?
Isn't it represented as a vector with components u, v, and w?
Exactly! We have u for the x-direction, v for the y-direction, and w for the z-direction. This allows us to analyze flow in three dimensions. Now, can anyone explain what happens to the time component in steady flow?
In steady flow, the velocity does not change over time, so we only consider spatial variables.
Correct! In steady problems, time components are not part of the solution, simplifying our analysis of fluid dynamics.
So is that why we can focus mainly on the pressure and velocity fields?
Exactly! Those are the core elements we look at to solve fluid mechanics problems.
Understanding Streamlines, Pathlines, and Streaklines
Unlock Audio Lesson
Now that we understand velocity fields, let's discuss streamlines, pathlines, and streaklines. First, what is a streamline?
A streamline is a line that is tangent to the velocity vector at every point in the flow.
Excellent! This means if you were to draw the streamline, it would show the direction a fluid particle would flow at a specific time. What about pathlines?
Pathlines show the paths taken by fluid particles over time, right?
Correct! And how would streaklines differ from pathlines?
Streaklines indicate the trajectories of particles that have passed through a certain point, like dye injected into the flow.
Absolutely right! All these lines help in visualizing the complex flow patterns we encounter. Remember, in steady flow, they all coincide.
Applications and Methods in Fluid Mechanics
Unlock Audio Lesson
Let's talk about the applications of these concepts. Why do you think understanding fluid flow lines is important?
It helps us predict how fluids behave in different scenarios, like around objects.
Exactly! We can apply this knowledge in various fields, from aerospace to civil engineering. What methods do we use to analyze fluid problems?
We can use analytical, experimental, and computational methods!
Great! Each method serves its purpose, especially in predicting weather patterns or designing vehicles. Why do computational methods have an edge these days?
They help us solve complex problems efficiently and accurately.
Exactly! Computational fluid dynamics has revolutionized how we approach these challenges.
Pressure Fields in Fluid Flow
Unlock Audio Lesson
Now, let's incorporate pressure fields into our discussion. How does pressure impact fluid flow?
Pressure gradients drive the fluid from high to low energy areas, affecting the flow direction.
Correct! Understanding how pressure changes spatially can help predict flow behavior. What's an example where pressure is critical?
Cavitation in fluid systems, where low pressure can cause liquid to vaporize.
Good example! Low pressure zones can lead to significant issues in engineering applications, which is why we closely monitor pressure fields.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the characteristics of streamlines and their importance in analyzing fluid flow, including definitions of velocity fields, pressure distributions, and the roles of various flow lines such as streamlines, pathlines, and streaklines. Additionally, it touches upon the use of analytical, experimental, and computational methods in fluid mechanics.
Detailed
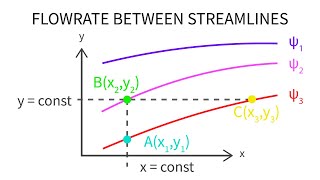
Streamlines
The concept of streamlines is essential in fluid mechanics as it provides a visual representation of the velocity of fluid at any given point in space. In fluid flow problems, it is vital to consider velocity fields (u, v, w) that depend on Cartesian coordinates and encapsulate how fluid moves. The pressure distribution is also crucial as it affects flow direction and intensity.
Key Points
- Velocity Field: Represents how the velocity varies as a vector field in space and time. The velocity can be resolved into its components along different axes, such as x, y, and z (u, v, w).
- Streamlines, Pathlines, and Streaklines:
- Streamlines indicate the direction of the velocity at any point in time. They are tangent to the velocity vectors, showing the trajectory fluid particles would follow at that instant.
- Pathlines represent the actual path traveled by a particle in the fluid over time.
- Streaklines are formed by all the fluid particles that pass through a specific point at different times.
The analysis of these flow lines assists in visualizing and solving complex fluid flow problems. The chapter further elaborates on the need for different methods (analytical, experimental, and computational) to address fluid dynamics effectively.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Velocity and Pressure in Fluid Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So for a very simple case, we can get analytical solutions like u and v and w and the pressure and that analytical solutions can help us to know the velocity, the pressure distribution of these problems and it satisfies conservation equations, mass conservation equations, linear momentum equations. Also, it satisfies the boundary conditions at the floor also flow inject what is coming it.
Detailed Explanation
In fluid dynamics, we can derive analytical solutions for various velocity components (u, v, w) and pressure. These solutions allow us to understand how fluid flows in different situations. Analytical solutions also ensure that certain laws, like the conservation of mass and momentum, are upheld. For example, in a flowing river, we can predict how fast the water will move and how the pressure will distribute along the riverbed based on these equations.
Examples & Analogies
Think of a water slide; the faster you go down (velocity), the more pressure you feel against your back. Analyses of how the water flows on the slide can predict speed and pressure distribution just like in fluid dynamics.
Velocity Field Definition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The velocity field, when we are talking about we are talking about this velocity as a vector quantity, which varies in space in case of the Cartesian coordinate system of x, y, z and the time. But most often for easy point of view, we resolve this velocity vector component into its scalar component in Cartesian coordinate systems like the i and j and k.
Detailed Explanation
A velocity field describes how the speed and direction of fluid flow change from one point to another in space. It is represented as a vector, which means it has both magnitude (speed) and direction. In a three-dimensional space (x, y, and z axes), the velocity components are typically expressed in terms of unit vectors in these directions (i, j, k) to ease calculations and visualizations.
Examples & Analogies
Imagine a snow globe. As you move the globe, the snowflakes (representing particles of fluid) drift through different layers of water (representing the velocity field). Each snowflake moves at different speeds and angles, which we can represent using coordinate systems.
Understanding Streamlines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A streamline is a line everywhere tangent to the velocity vector at a given instant. That means time equal to zero or we take a snapshot. At each point, if I draw this the tangent, that tangent should give directions of the velocity vector.
Detailed Explanation
Streamlines visually represent fluid flow. If you were to take a still image of the fluid at a moment in time, the lines you draw that are tangent to the flow's velocity vectors are called streamlines. They show how fluid moves without mixing and help predict the future positions of particles in the flow.
Examples & Analogies
Think of a school of fish swimming together in a pond. If you paused the water and took a picture, the invisible lines showing the paths the fish took would look similar to streamlines. They represent how and where the fish move in relation to each other without clashing.
Pathlines and Streaklines Explained
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Pathline is the actual path traversed by a given fluid particle. A streakline is the locus of the particles that have earlier passed through a prescribed point.
Detailed Explanation
Pathlines illustrate the journey of individual fluid particles over time, reflecting how they move within a flow. Streaklines, conversely, show the path that particles have taken through a specific point in space over time. They help visualize how fluid moves from one location to another, which can be particularly useful in experimental situations, such as dye injection in a flowing river.
Examples & Analogies
Consider a ribbon being waved in the wind. If you let go of the ribbon at one point, the path it took while flying through the air represents a pathline. Now, if you were to apply colored spray paint at the same point, the trail left by the spray represents streaklines, showing where particles exited from that location.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Velocity Field: A representation of the velocity of fluid components in a given direction.
-
Streamline: A visual representation of flow, indicating the direction fluid particles travel.
-
Pathline: The actual path a particle follows over time in the fluid.
-
Streakline: Indicates the locus of fluid particles from a single point over time.
-
Pressure Gradient: The change in pressure that can drive the fluid flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A weather radar setup examining the wind flow illustrates how streamlines direct airflow around structures.
-
Color dye visualization in water flow helps to demonstrate streaklines as particles move through a point.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Fluid flows in ways so fine, streamlines show the path, that's the line.
📖 Fascinating Stories
-
Imagine a river flowing around a rock. The water curves and bends, creating invisible lines that guide its movement—this is the essence of streamlines.
🧠 Other Memory Gems
-
Remember S-P-S: Streamline, Pathline, and Streakline are essential for understanding fluid flow.
🎯 Super Acronyms
V-P-S
- Velocity field
- Pressure gradient
- Streamline.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Streamline
Definition:
A line that is tangent to the velocity vector at every point in a fluid flow at a given instant.
-
Term: Pathline
Definition:
The actual path traced by a fluid particle as it moves through the flow field over time.
-
Term: Streakline
Definition:
A line that represents all the particles that have passed through a specified point over time.
-
Term: Velocity Field
Definition:
A representation of how the velocity of a fluid varies in three-dimensional space.
-
Term: Pressure Gradient
Definition:
The rate of change of pressure in a fluid flow field, which influences the flow direction.