Temperature Gradients
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Temperature Gradients
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will discuss temperature gradients and their significance in fluid dynamics. Can anyone tell me what they think a temperature gradient is?

Is it how quickly the temperature changes over a distance?

Exactly right, Student_1! A temperature gradient indicates how temperature varies with position. It plays a crucial role in affecting fluid behavior. Why do you think this is important in fluid mechanics?

Because it might affect how fast the fluid moves or its pressure?

Correct! The temperature gradient can influence both the velocity and pressure distributions within the fluid. Let’s remember this by using the acronym 'TIPS' – Temperature Influences Pressure and Speed.
Calculating Pressure and Velocity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's delve into how we can calculate pressure and velocity when we have a temperature gradient. Where do we start?

Do we use the mass conservation equations?

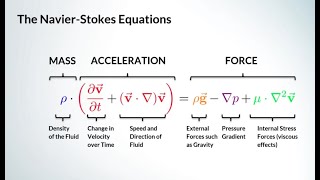
Yes, that's spot on! We need to apply mass and momentum conservation equations to derive the relationships between temperature, pressure, and velocity in a fluid flow problem. This is vital for ensuring that we maintain conservation laws.

So we use equations to predict how fluids behave based on their temperatures?

Exactly! These equations help us understand the functional relationships of velocity components with respect to the coordinates x, y, and z.
Real-World Examples of Temperature Gradients in Fluid Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's consider some examples to see these concepts in action. Can anyone think of an example?

What about wind flow over a weather radar?

Great! In that case, the temperature gradients can significantly influence wind velocity and pressure patterns around the radar setup. What about another example?

A jet of water hitting the floor could be another one.

Exactly! Both examples show how temperature differences can alter fluid dynamics, which is critical in real-life applications, such as weather forecasting and understanding ocean currents.
Experimental vs Analytical Methods
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

We have talked about how to predict temperature gradients theoretically. How about in practice?

Would that be experimentation?

Exactly! We can use experimental methods to validate our analytical predictions. Which approach do you think is more beneficial?

I think both are important because experiments provide real-world data, while analytical methods help us understand the underlying principles.

Correct! The combination of both methods allows for a comprehensive understanding of complex flow situations. Remember to consider physical models as well for testing.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section discusses temperature gradients, highlighting how they influence fluid dynamics through pressure and velocity distributions, and the necessity of applying conservation equations to analyze flow. It explores both analytical and experimental methods to understand these relationships with real-world examples.
Detailed
In this section, we delve into the concept of temperature gradients and their role in fluid dynamics. Temperature gradients are defined as the rate at which temperature changes with respect to spatial coordinates. Understanding these gradients is vital for analyzing fluid behavior under varying thermal conditions. The section highlights how the flow characteristics are significantly affected by pressure and velocity distributions derived from the analytical solutions of mass and momentum conservation equations. Additionally, the importance of recognizing boundary conditions and utilizing both experimental and computational methods to visualize complex flow patterns is emphasized. Two examples are provided: wind flow over a weather radar setup and a jet impact on a floor, to contextualize these principles in practical scenarios.
Youtube Videos

![[CFD] What are Thermal (Temperature) Wall Functions?](https://img.youtube.com/vi/2bJ-5gaeSE0/mqdefault.jpg)






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fluid Flow and Temperature Gradients
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So for a very simple case, we can get analytical solutions like u and v and w and the pressure, and that analytical solution can help us to know the velocity, the pressure distribution of these problems and it satisfies conservation equations, mass conservation equations, linear momentum equations.
Detailed Explanation
In fluid dynamics, we can derive analytical solutions for the velocity components (u, v, w) and the pressure in a fluid. These solutions help to understand how these variables are distributed within the fluid flow, and they must also satisfy the principles of physics, such as mass conservation and momentum equations. This analytical approach provides a foundational understanding of how fluid moves and behaves under different conditions.
Examples & Analogies
Think of it like understanding traffic flow on a road: by looking at speed limits (which resembles velocity distribution), we can predict where cars will be positioned at given times, similar to how we can predict fluid pressure and velocity in a flow.
Simplifying the Problem
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Also, it satisfies the boundary conditions at the floor also flow inject what is coming in.
Detailed Explanation
When we simplify fluid flow problems, we assume that the flow can be represented in two dimensions and that it is incompressible and steady. This means the fluid's density remains constant and does not change over time. We consider boundary conditions, which are constraints at the surfaces where the fluid interacts with solid boundaries, like the ground. These assumptions help to streamline calculations and make finding solutions more feasible.
Examples & Analogies
Imagine trying to model the flow of a river. By only considering the surface flow and ignoring deeper currents or the water changing over time, we can create a more manageable model to predict where the water will go.
Components of the Velocity Field
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We define a velocity field and resolve the velocity vector component into its scalar components in Cartesian coordinate systems like the i, j, and k. This means you will have the u velocity components along the x direction, v in the y direction, and w in the z direction.
Detailed Explanation
The velocity field of a fluid is described as a vector that has three components (u, v, w) corresponding to the three dimensions in space (x, y, z). By breaking down the vector into these scalar components, we can analyze the flow more easily in specific directions. This helps us understand how the fluid is moving throughout the entire space in which it exists.
Examples & Analogies
Think of a balloon being blown up: the air inside is moving in multiple directions (up, down, side to side) at the same time. By measuring how fast the air is moving in each direction, we can fully describe the balloon's air movement in three-dimensional space.
Pressure Distribution in Fluid Flow
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now I am just defining them the velocity field... the pressure distribution plays major roles because the flow comes from high energy to the low energy.
Detailed Explanation
Pressure in fluids influences how and where they flow. Fluids naturally move from areas of high pressure (high energy) to low pressure (low energy). Understanding pressure distribution is essential because it determines the directions in which fluid flows—this understanding is guided by pressure gradients, which are differences in pressure across distances.
Examples & Analogies
Consider a water slide: as you start at the top (high pressure), you naturally flow down to the bottom (lower pressure). The pressure difference is what propels you along the slide.
Temperature and Density in Fluid Mechanics
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you know the velocity field and pressure variations, you have solved that fluid flow problems. But when you have the heat exchange going on drastically in fluid flow where there is a lot of temperature gradients, apply the first law of thermodynamics to get the temperature field.
Detailed Explanation
When fluids exchange heat, temperature gradients arise that can affect fluid behavior. To assess these changes, the first law of thermodynamics is applied to evaluate how heat transfer influences the temperature field within the fluid. This becomes important especially in systems with significant heat exchange, as it can impact flow characteristics, including density.
Examples & Analogies
Imagine a hot cup of coffee sitting in a cold room. The heat from the coffee transfers to the coffee cup and the surrounding air, creating a gradient where the bottom of the cup is warmer than the top. This temperature gradient affects how the coffee behaves compared to if it were at a uniform temperature throughout.
Key Concepts
-
Temperature Gradients: The rate of temperature change per unit distance directly influences fluid behavior.
-
Velocity Field: Describes how fluid velocities vary with position over time and is key to flow analysis.
-
Pressure Distribution: The spatial variation of pressure in fluid dynamics, essential for understanding how fluid flow behaves.
Examples & Applications
Wind flow over a weather radar, where temperature gradients impact wind velocity.
Jet interaction with a floor, which demonstrates the effects of pressure and temperature on fluid movement.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Temperature flows east and west, affecting velocity is its quest.
Stories
Imagine a river where warm water meets cool water; they mix and change flow patterns. This illustrates how temperature gradients alter fluid dynamics.
Memory Tools
TIPS – Temperature Influences Pressure and Speed.
Acronyms
VPP – Velocity, Pressure, and Position are key components in fluid flow analysis.
Flash Cards
Glossary
- Temperature Gradient
The rate of temperature change per unit distance in a specific direction.
- Velocity Field
A vector field that represents the velocity of fluid particles at different points in space.
- Pressure Distribution
The variation of pressure throughout a fluid field, influenced by velocity and temperature.
Reference links
Supplementary resources to enhance your learning experience.
