Velocity Field
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introducing Velocity Field
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll discuss the velocity field. What do you think a velocity field represents in fluid mechanics?

Is it about how fast the fluid is moving in different directions?

Exactly! It's a vector quantity that describes the velocity at different points in space and time. We represent it using components u, v, and w for x, y, and z directions respectively, forming the vector field.

So, it's like having a different speed for each direction?

Yes! It's crucial in both analytical and experimental studies of fluid flow. Can anyone recall why knowing these velocities is important?

Because it helps us understand pressure distribution?

Correct! The velocity and pressure fields are interconnected and essential for solving fluid dynamics problems.

To summarize, a velocity field is crucial for analyzing flow behavior. It's represented as a vector containing scalar components u, v, and w.
Methods of Determining Velocity Fields
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Moving on, let's explore how we determine velocity fields. Can anyone name methods used?

We can use analytical methods, right?

Right! Analytical methods provide solutions for simple flow cases. But what about more complex scenarios?

Maybe experimental methods?

Exactly! Experimental methods help visualize flow in real-time. Additionally, computational fluid dynamics is crucial for complex problems.

How does computational methods help exactly?

They simulate fluid flow under various conditions, which helps engineers and scientists in design and analysis.

In summary, determining velocity fields can be achieved through analytical, experimental, and computational methods, each suited for different complexities.
Pressure Gradient and Flow Dynamics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's connect velocity fields with pressure gradients. Why do we think pressure gradients are important for fluid flow?

Is it because flow moves from high to low pressure areas?

Exactly! The flow direction is driven by pressure gradients, and understanding this can help predict flow patterns.

So, if pressure drops suddenly, does that affect velocity?

Yes! A sudden decrease in pressure can increase flow velocity, potentially leading to phenomena like cavitation.

Let’s recap: pressure gradients significantly influence fluid flow dynamics, dictating how and why fluids move.
Flow Visualization Techniques
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

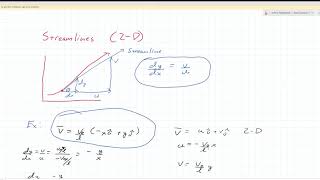
Now we’ll look at visualizing flow using streamlines, pathlines, and streaklines. What differentiates these terms?

Streamlines show direction at a moment, right?

Exactly! Streamlines connect points of fluid velocity at a given instant. What about pathlines?

Those are the actual paths particles take, right?

Correct! And streaklines show where particles have passed through a specific point over time.

Why are these concepts useful?

They help us visualize and predict flow patterns around objects, which is crucial in engineering designs.

To summarize, streamlines, pathlines, and streaklines are effective tools for analyzing fluid flow and its behavior.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The velocity field is a crucial concept in fluid mechanics, represented as a vector quantity that varies in space and time. This section discusses how to determine velocity fields analytically and experimentally, the relationship between velocity and pressure gradients, and the importance of understanding flow patterns through visualizations like streamlines, pathlines, and streaklines.
Detailed
Velocity Field
The velocity field in fluid mechanics represents the velocity at various points in a fluid and is expressed as a vector quantity varying in space and time. It can be resolved into three scalar components: u, v, and w, representing velocities in the x, y, and z directions respectively, thereby establishing a functional relationship with Cartesian coordinates (x, y, z, t).
Key Points Covered:
- Analytical Solutions: For simple cases, analytical solutions can provide information about velocity and pressure distributions, adhering to mass conservation and linear momentum equations.
- Pressure and Velocity Relationships: The section implies that the velocity field's behavior is strongly influenced by pressure gradients, with flow patterns changing in response to pressure variations.
- Flow Visualization: Concepts like streamlines, pathlines, and streaklines are introduced to visualize flow and understand how fluid particles behave over time. These visualizations help in analyzing flow conditions around structures (like weather towers) or complex geometries (like birds).
- Experimental and Computational Methods: The determination of velocity fields may involve various methods, including experimental and computational approaches, providing an accurate representation of real-time fluid dynamics.
Understanding these elements is essential for solving complex fluid flow problems and visualizing flow patterns, which aids in practical applications across various engineering disciplines.
Youtube Videos
![Introduction to Velocity Fields [Fluid Mechanics #1]](https://img.youtube.com/vi/CkNo5xGMZS4/mqdefault.jpg)





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Velocity Field
Chapter 1 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So for a very simple case, we can get analytical solutions like u and v and w and the
pressure and that analytical solutions can help us to know the velocity, the pressure
distribution of these problems and it satisfy conservation equations, mass conservation
equations, linear momentum equations.
Detailed Explanation
In fluid mechanics, we can derive analytical solutions for velocity (u, v, w) and pressure in a fluid flow. These solutions are valuable because they help us understand how velocity and pressure are distributed in a flow system. The solutions must also satisfy the conservation laws, which include mass conservation and linear momentum equations. Essentially, these laws ensure that mass and momentum are conserved in a flowing fluid.
Examples & Analogies
Think of a flowing river. Just as water moves from a higher elevation to a lower one, fluid dynamics must obey certain rules—like maintaining a consistent volume (mass conservation) and moving steadily without sudden jerks (momentum conservation).
Simplifying Assumptions
Chapter 2 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We can simplify it and we can like it a two-dimensional incompressible steady flow, this is what the total simplification of problems or these assumptions are hold good for these type of problems.
Detailed Explanation
To analyze fluid flow more easily, we often simplify the problem by assuming two-dimensional flow (meaning the fluid moves in only two directions, like left/right and up/down) that is incompressible (the fluid's density does not change). These assumptions make it easier to apply mathematical equations to find solutions for velocity and pressure.
Examples & Analogies
Imagine a flat, calm pond where you throw a stone. The ripples created can be seen as two-dimensional waves, and if we consider the water's density to remain constant, it simplifies understanding how the waves travel outward.
Understanding Velocity Components
Chapter 3 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
How to get this u and v equations and the pressure that what we will discuss later, but at present you know that we can get it the functional relationship of u, v with respect to a Cartesian coordinate of x, y, z and these problems becomes a steady problem.
Detailed Explanation
We can express the velocity components (u, v, w) as functions of spatial coordinates (x, y, z) and time (t). In a steady flow, the fluid properties at any fixed point do not change over time, allowing for clearer determination of how velocity varies with respect to position in space.
Examples & Analogies
If you imagine pushing a toy car along a table, the car's speed and direction change based on where you push it. Measuring where the car is (x, y coordinates) at any moment gives you a clear relationship between its position and speed—just like we relate velocity components to coordinates in fluid dynamics.
Defining the Velocity Field
Chapter 4 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
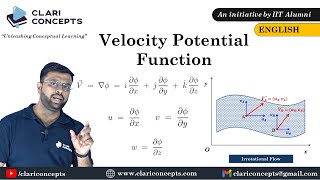
When we are talking about we are talking this velocity as a vector quantity, which vary in a space in case of the Cartesian coordinate system of x, y, z and the time. But most often for easy point of view, we resolve this velocity vector component into its scalar component in Cartesian coordinate systems like the i and j and k.
Detailed Explanation
The velocity field in fluid mechanics is described as a vector quantity, meaning it has both magnitude (speed) and direction, which varies in space (x, y, z) and over time (t). Typically, we break this vector down into its scalar components. In Cartesian coordinates, these components are represented as u (x-direction), v (y-direction), and w (z-direction).
Examples & Analogies
Think of driving a car. Your speed (magnitude) and steering direction (angle) represent your velocity. When determining your position on a grid (like a map), you can break this down into components: moving forward (u), turning left (v), and changing altitude if you're flying (w).
Velocity Field Equation
Chapter 5 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
V(x, y, z, t) = u(x, y, z, t) + v(x, y, z, t) + w(x, y, z, t)
Detailed Explanation
The velocity field can be mathematically expressed by combining the individual velocity components at any point in the three-dimensional space and at a given moment in time. This equation helps us visualize how the total velocity at any point is affected by its components u, v, and w.
Examples & Analogies
Consider a flowing river. The total speed of the water at a specific location can be seen as the combination of different currents pushing the water in various directions. Each current adds up to give you the water's overall behavior at that point.
Pressure in Fluid Flow
Chapter 6 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now as already I discussed that we talk about the pressures which is very dynamic variables, the pressure distribution play the major roles because as you know it the flow is come from high energy to the low energy.
Detailed Explanation
Pressure in fluid flow is a crucial factor because it indicates where and how the fluid moves. Typically, fluids flow from areas of higher pressure (or high energy) to areas of lower pressure. Understanding pressure distribution helps predict the fluid's behavior in various conditions.
Examples & Analogies
Consider a balloon. If you press on one side, the air inside moves to an area where there's less pressure (the open space) because the push from the higher pressure causes it to flow. Similarly, understanding pressure in fluids helps engineers design systems that manage fluid flow effectively.
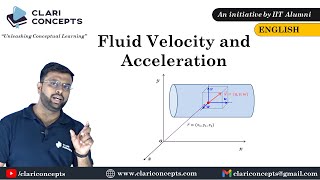
Computing Acceleration from Velocity Field
Chapter 7 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If I know the velocity field, we can compute it what will be the acceleration, the rate of change of the velocity gradient, velocity.
Detailed Explanation
Once we have established the velocity field, we can determine the acceleration by calculating how the velocity changes over time and across different points in the fluid. This change in velocity is essential for understanding the motion of the fluid.
Examples & Analogies
Think of a car speeding up at a stoplight. The faster it accelerates (the change in speed), the more quickly it covers distance. Similarly, in fluids, examining changes in speed allows us to understand how quickly and effectively the fluid is moving.
Key Concepts
-
Velocity Field: A vector field denoting fluid flow speed and direction.
-
Pressure Gradient: Affects flow direction based on high to low pressure areas.
-
Flow Visualization: Techniques such as streamlines, pathlines, and streaklines for understanding fluid behavior.
Examples & Applications
A weather radar setup where the wind flow creates a velocity field affecting measurements.
A water jet impacting a surface demonstrating changes in velocity and pressure dynamics.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In velocity fields, we see, flows of air and liquid free, speed in layers, depth holds key, where pressure shifts, we flow with glee.
Stories
Imagine a river, flowing fast at the surface but slow at the bottom. This illustrates how velocity varies in the water, just like in a velocity field.
Memory Tools
Remember 'V-Pressure-Flow' for visualizing how velocity fields relate pressure gradients to flow dynamics.
Acronyms
VPS
Velocity
Pressure
Streamlines—these key terms guide our understanding of fluid flow.
Flash Cards
Glossary
- Velocity Field
A vector representation of fluid velocity at various points in space and over time.
- Pressure Gradient
The rate of pressure change in a fluid, impacting flow direction and velocity.
- Streamline
A line that is tangent to the velocity vector of the fluid at any given instant.
- Pathline
The trajectory followed by a specific fluid particle over time.
- Streakline
The locus of all fluid particles that have passed through a specified point at some time.
Reference links
Supplementary resources to enhance your learning experience.
