Pressure and Velocity Fields
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Velocity Fields
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're exploring velocity fields in fluid dynamics. Can anyone tell me what the velocity field represents?

Is it about how fast the fluid is moving in different directions?

That's correct! The velocity field represents how the velocity of the fluid varies in space. Specifically, we express it in Cartesian coordinates as V(x, y, z, t) = u i + v j + w k. Who can explain what these components mean?

u is the velocity in the x-direction, v in the y-direction, and w in the z-direction, right?

Exactly! Each component can be a function of space and time. Remember, it’s crucial for analyzing flow in different scenarios.

What do we need the velocity field for?

Good question! Knowing the velocity field helps us compute acceleration and understand how fluid flows in complex systems. It's essential to visualizing fluid movement.

What is acceleration in this context?

Acceleration can be derived from the velocity field and indicates how quickly the fluid’s speed or direction is changing. We'll dive deeper into this shortly!

To summarize, the velocity field defines the flow characteristics of fluids and is essential for derived calculations. Keep these definitions in mind!
Pressure Distribution
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s talk about pressure distribution within fluid mechanics. Does anyone know why pressure is significant?

It affects how fluids move, right?

Exactly! Pressure gradients drive fluid flow from areas of high energy to low energy. Can anyone explain what can occur if pressure drops significantly?

Cavitation can happen, right? Water turns into vapor due to low pressure.

Exactly! That's a crucial point in fluid mechanics. Understanding pressure and its gradients helps us predict fluid behavior in various conditions. We often analyze how pressure changes over time and space.

So, how do we calculate pressure in practice?

We typically use equations that consider both velocity fields and boundary conditions. It's a combination of theoretical and practical application.

This can be complex, can't it?

Yes, as flow fields become more complex, analyzing pressures and velocities becomes more intricate. To summarize, understanding pressure fields is fundamental for manipulating and predicting fluid behavior.
Flow Visualization: Streamlines, Pathlines, and Streaklines
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's wrap up with flow visualization. Who can tell me the differences among streamlines, pathlines, and streaklines?

Streamlines show the direction of the fluid at a specific moment.

Pathlines show the trajectory of a fluid particle over time.

And streaklines indicate where particles have passed through a fixed point.

Great! Visualizing these lines is crucial for understanding flow patterns and predicting how fluids behave in systems. Why do you think visualizing flow is important?

It helps us design better systems and improve efficiency, right?

Exactly! Visual aids enable us to simplify complex fluid dynamics into understandable patterns. So remember: streamlines represent instantaneous flow, pathlines represent actual particle paths, and streaklines show the history of particles through a point.

To sum up, these visualizations foster better comprehension of fluid motion and help engineers solve real-world problems effectively.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section discusses how analytical solutions for pressure and velocity components can model fluid flow while satisfying conservation equations. It introduces concepts such as velocity fields defined in Cartesian coordinates, the importance of pressure gradients, and challenges in visualizing complex fluid flows.
Detailed
Detailed Summary
This section on Pressure and Velocity Fields dives into the essential analytical solutions for understanding fluid mechanics. It begins by explaining how simplified assumptions, such as considering two-dimensional incompressible steady flow, allow us to derive equations for velocity components (u, v, w) and pressure distributions in a fluid. These solutions are vital in satisfying mass conservation and linear momentum equations.
Key Components of Fluid Flow
- Velocity Field: The velocity is a vector quantity defined in a Cartesian coordinate system (x, y, z) that is broken down into scalar components (u, v, w). The velocity can be expressed as:
V(x, y, z, t) = u(x, y, z, t) i + v(x, y, z, t) j + w(x, y, z, t) k
Understanding this velocity field is crucial for calculating acceleration and analyzing fluid dynamics.
- Pressure Field: Pressure is a dynamic variable that can indicate flow direction due to pressure gradients. The section discusses how pressure affects fluid behavior and can lead to phenomena like cavitation, occurring when pressure drops below a liquid's vapor pressure.
- Visualizing Flow Patterns: The lecture introduces different forms of lines used in flow visualization: streamlines, pathlines, and streaklines. Streamlines are tangential to the velocity vector at a given moment, whereas pathlines trace the trajectory of particles over time and streaklines mark the locus of particles passing through a specific point.
These principles help us understand fluid behavior in complex systems, like airflows over structures and jets impacting surfaces, laying the groundwork for both experimental methods and computational fluid dynamics.
Youtube Videos
![Introduction to Velocity Fields [Fluid Mechanics #1]](https://img.youtube.com/vi/CkNo5xGMZS4/mqdefault.jpg)



![[CFD] The PISO Algorithm](https://img.youtube.com/vi/ahdW5TKacok/mqdefault.jpg)



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Pressure and Velocity Fields
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So for a very simple case, we can get analytical solutions like u and v and w and the pressure, and that analytical solutions can help us to know the velocity, the pressure distribution of these problems and it satisfies conservation equations, mass conservation equations, linear momentum equations. Also, it satisfies the boundary conditions at the floor as well as flow inject what is coming in.
Detailed Explanation
This chunk introduces the concept of pressure and velocity fields in fluid dynamics. It explains that for simple cases, analytical solutions can be obtained for velocity components (u, v, w) and pressure. These solutions adhere to conservation laws, meaning they respect the principles of mass and momentum conservation, which are fundamental to fluid motion. Additionally, boundary conditions, which represent the constraints on the flow at surfaces like the ground, are also addressed.
Examples & Analogies
Imagine water flowing smoothly from a garden hose. In this simple flow scenario, we can predict how fast the water will exit the hose (velocity) and how much pressure is needed to push that water out. This prediction relies on understanding conservation laws, just like how we can predict how much water is in a tank by applying the principle of conservation of water.
Two-Dimensional Incompressible Steady Flow
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So we can simplify it and consider it as a two-dimensional incompressible steady flow, which is the total simplification of problems where these assumptions hold good. Then, you apply the mass conservation linear momentum equations, and you get these solutions.
Detailed Explanation
This chunk emphasizes the simplification process in fluid dynamics by focusing on a specific type of flow: two-dimensional, incompressible, and steady. In this scenario, fluid density remains constant, and conditions do not change with time. By applying the mass conservation and momentum equations, we can derive meaningful solutions that describe the behavior of the flow in this simplified model, making it easier to analyze.
Examples & Analogies
Think of how air behaves when you blow gently into a balloon. If you keep the balloon still, the air inside doesn't change over time (steady), and the air takes up a constant volume (incompressible). This steady, two-dimensional flow can be analyzed simply using the principles of fluid dynamics.
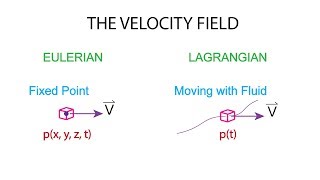
Defining the Velocity Field
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When we talk about the velocity field, we are discussing velocity as a vector quantity that varies in space concerning the Cartesian coordinate system of x, y, z, and time. We resolve this velocity vector into its scalar components in Cartesian coordinates like i, j, and k.
Detailed Explanation
Here, we explore the concept of a velocity field, which describes how velocity changes across a space defined by the Cartesian coordinate system (x, y, z) over time. Velocity, being a vector, can be broken down into its components (u along x, v along y, and w along z). Understanding how these components vary in space and time is crucial for modeling fluid motion accurately.
Examples & Analogies
Imagine a basketball moving in a three-dimensional space. It has speed and direction at every point along its path. In the same way, fluid particles have velocity defined by their direction and speed in a 3D space—much like tracking where the basketball bounces as it moves.
Pressure in Fluid Flow
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Pressure is a dynamic variable, and the pressure distribution plays a major role because the flow comes from high energy to low energy. The pressure gradients indicate which direction the flow will take, making computing pressure and pressure gradients a major component in fluid flow problems.
Detailed Explanation
This chunk discusses pressure as a variable that changes throughout fluid flow. Pressure differences, or gradients, drive fluid movement from areas of high energy (and pressure) to low energy (and pressure). Being able to calculate the pressure distribution in a fluid flow is essential for predicting how and where the fluid will move.
Examples & Analogies
Consider a water slide. The water at the top has high pressure due to its height (potential energy) and flows down to the bottom where the pressure is lower. This pressure difference makes the water flow smoothly down the slide. Thus, understanding pressure distribution helps us predict the flow of the water.
Density and Its Role in Fluid Dynamics
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The density plays a major role in flow behavior, as it describes mass per unit volume. In compressible flows, density varies with position and time, while it is nearly constant for liquids. The relationship between density and pressure is crucial, especially when considering flows at different speeds.
Detailed Explanation
In this chunk, we look at density as a key property of fluids that influences flow characteristics. It is defined as mass per unit volume. In compressible flows, density can change depending on the fluid's position and time, while for most liquids, it remains constant. Understanding these variations allows us to predict how fluids will behave under various conditions, particularly with respect to pressure.
Examples & Analogies
Imagine a balloon filled with air. If you squeeze it, you increase the pressure, and the density of the air inside the balloon increases as well. This change in density affects how the air flows out of the balloon when you release it. Similarly, understanding how density changes in fluids helps us manage their flow.
Visualization of Flow Patterns
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
To visualize fluid flow, we define three types of lines: streamlines, pathlines, and streaklines. Streamlines show the direction of the velocity vector at a specific instant, pathlines represent the path of a fluid particle over time, and streaklines are the locus of particles that have passed through a specific point.
Detailed Explanation
This chunk introduces the three key concepts of flow visualization: streamlines, pathlines, and streaklines. Streamlines indicate the direction of fluid flow at a specific moment, while pathlines show the actual trajectory of a fluid particle over time. Streaklines depict particles that have traveled through a defined point. These concepts are fundamental for understanding how fluids move and can be visualized.
Examples & Analogies
Picture a river with boats. Streamlines could represent the direction the boats point at a given time, pathlines trace the actual journey of each boat, and streaklines would be like a trail of leaves that have floated down to the same spot on the riverbank, showing where the water was flowing.
Key Concepts
-
Velocity Field: Represents the distribution of fluid velocities over space and time.
-
Pressure Field: Defines how pressure varies in a fluid, influencing flow direction.
-
Streamlines: Lines indicating fluid flow direction at a specific moment.
-
Pathlines: Paths traced by individual fluid particles over time.
-
Streaklines: Lines representing the history of fluid particles passing through a specific point.
Examples & Applications
Example of a velocity field showing air flowing over a weather radar setup, demonstrating varying speeds at different points.
A jet impacting a surface illustrates pressure distribution and potential for cavitation in areas of low pressure.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Pressure leads the flow, from high to low, cavitation’s a foe, where liquids go slow.
Stories
Imagine a river flowing harshly as the tight banks reduce its width. As a narrow section appears, the pressure drops, leading to cavitation where the water vaporizes, showing how essential pressure distribution is in fluid flow.
Memory Tools
VPS - Velocity, Pressure, Streamlines: Remember these key concepts when analyzing fluid dynamics.
Acronyms
FPS - Fluid Pressure and Speed
reminder of the key components in understanding pressure and velocity fields.
Flash Cards
Glossary
- Velocity Field
A representation of the velocity of fluid particles at different points in space and time.
- Pressure Field
The distribution of pressure in a fluid, often determining flow direction and behavior.
- Streamline
A line that is tangent to the velocity vector at a given instant, illustrating fluid flow direction.
- Pathline
The trajectory followed by a fluid particle over time.
- Streakline
The locus of particles that have passed through a prescribed point in the flow.
- Cavitation
The formation of vapor cavities in a liquid due to low pressure, potentially leading to damage.
Reference links
Supplementary resources to enhance your learning experience.
