Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Analytical Solutions
Unlock Audio Lesson
Today, we’re going to discuss how analytical solutions help us understand fluid flow. Can anyone tell me what we mean by analytical solutions?
I think it’s when we use equations to describe the flow?
Exactly! Analytical solutions provide us with equations for velocity and pressure distributions in flow conditions. For instance, in simple cases, we can represent u, v, and w functions analytically. What do these symbols represent?
U is the velocity in the x direction, v in the y direction, and w in the z direction.
Correct! These solutions must also satisfy mass and momentum conservation equations. Can anyone explain what those are?
The mass conservation equation ensures that mass is preserved in the flow, right?
That's right! And the momentum equation relates to how the velocity changes in response to pressure gradients. Remember, we often simplify our problems to two-dimensional incompressible steady flows for easier analysis.
So in summary, analytical solutions provide a mathematical framework to predict parameters of flow, satisfying key conservation equations.
Flow Visualization Techniques
Unlock Audio Lesson
Now that we understand analytical solutions, let’s dive into flow visualization techniques. What are some ways we can visualize fluid flow?
We can use streamlines, pathlines, and streaklines.
Yes! Let’s discuss streamlines first. What are they?
Streamlines are lines that are tangent to the velocity vector. They show the direction of fluid flow at any instant.
Perfect! And remember, mass does not cross streamlines. Now, how are pathlines different?
Pathlines are the actual paths taken by fluid particles over time.
Right! And what about streaklines?
Streaklines are made up of all the particles that have passed through a specific point in a flow.
Exactly! These visualization methods help us interpret flow patterns. Can anyone summarize how they interrelate?
In steady flow, streamlines, pathlines, and streaklines are the same since the flow properties don’t change over time.
Great summary! Visualizing these different lines aids in predicting how fluids behave in various systems.
Practical Applications of Fluid Flow Concepts
Unlock Audio Lesson
Let’s put our flow visualization knowledge to practical use. Can anyone think of a real-world example where understanding flow is crucial?
In aerodynamics, like designing airplane wings.
Absolutely! Understanding how air flows over wings can optimize performance. What should we consider in these scenarios?
The pressure distributions around the wings!
Very important! The pressure gradient influences lift. We visualize these using our concepts. What is one way we might do this experimentally?
Using dye to trace flows and see how they interact with the wing.
Yes! This is how streaklines can be employed in practice. Let’s remember that visualizing flow is not just theoretical but has direct applications in engineering and design.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section provides insight into how analytical solutions inform about pressure and velocity distributions in fluid flow, emphasizing mass conservation and momentum equations. It also introduces key visualization methods in fluid mechanics, including streamlines, pathlines, and streaklines, which help understand flow behavior in various scenarios.
Detailed
In fluid mechanics, understanding flow visualization is crucial for solving complex problems related to pressure and velocity distribution. The section begins with the description of obtaining analytical solutions for simple cases, allowing for the determination of velocity (, v, w) and pressure distributions while satisfying conservation equations such as mass conservation and linear momentum equations. High relevance is placed on simplifying conditions and considering two-dimensional incompressible steady-flow assumptions.
Key visualization methods are detailed:
1. Streamlines: Lines tangent to the velocity vector at any instant, indicating the direction of flow. No mass crosses through streamlines, making them useful for analyzing flow without disruption.
2. Pathlines: The actual trajectory a fluid particle takes over time—helpful for understanding movement dynamics.
3. Streaklines: The locus of particles that have passed through a specific point, often visualized using dye in experiments to trace previously traveled paths.
The discussion also emphasizes the significance of visualizing flow patterns for improved understanding and problem-solving in complex fluid dynamics scenarios.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Velocity Fields
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So now I am just defining them the velocity field, when we are talking about we are talking this velocity as a vector quantity, which vary in a space in case of the Cartesian coordinate system of x, y, z and the time. But most often for easy point of view, we resolve this velocity vector component into its scalar component in Cartesian coordinate systems like the i and j and k.
As you know from vector rotations of x and y, j these are the unit vectors. So you will have the u velocity components along this x direction, u(x, y, z, t) 𝑖. The v velocity components, v velocity component in y direction and w is a velocity component z. All will have a scalar component having a functions with the space x, y, z and the time; v = v(x, y, z, t) 𝑗 and w is w(x, y, z, t) 𝑘. So we define a velocity field.
V(x, y, z, t) = u(x, y, z, t) 𝑖 + v(x, y, z, t) 𝑗 + w(x, y, z, t) 𝑘.
Detailed Explanation
This chunk introduces the concept of a velocity field in fluid dynamics. A velocity field describes how the velocity of a fluid varies in three-dimensional space (x, y, z) over time. To clarify the vector nature of velocity, it can be broken down into its scalar components along the three axes (u, v, w), which represent velocities in the x, y, and z directions respectively. This decomposition simplifies calculations and helps in analyzing the fluid's behavior in different spatial directions.
Examples & Analogies
Imagine you're watching a river flow. At different points in the river (like in different x, y, z coordinates), the water might be moving at different speeds and directions. This is similar to how the velocity field works, tracking the speed and direction (velocity) of the water at these various locations.
Calculating Acceleration from Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Similar way if I know the velocity field, we can compute it what will be the acceleration, the rate of change of the velocity gradient, velocity, you know it the accelerations that the component you will get it.
Detailed Explanation
Knowing the velocity field allows us to calculate the acceleration of the fluid. Acceleration is the rate at which the velocity changes over time and space. By understanding how velocity changes with respect to both time and space, one can derive the acceleration field, which is crucial for analyzing fluid motion and behavior.
Examples & Analogies
Consider a car speeding up at different rates on a highway—sometimes it's going faster or slower. In fluid dynamics, just like watching the car's changes in speed (acceleration), we can track how a fluid's velocity changes at different points to understand its overall movement.
Dynamics of Pressure in Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
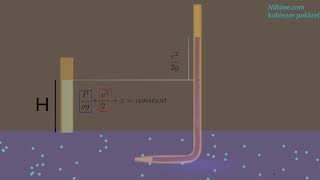
Now as already I discussed that we talk about the pressures which is very dynamic variables. The pressure distribution plays major roles because as you know it the flow comes from high energy to low energy. Many of the time this pressure gradient indicates for us which direction flow will be there.
Detailed Explanation
Pressure is a key variable in fluid dynamics, influencing the flow of fluids. Fluids naturally flow from areas of high pressure (high energy) to areas of low pressure (low energy). Understanding the principle of pressure gradients helps us predict the direction of fluid movement. Pressure distributions can indicate how and where fluid will flow depending on the conditions.
Examples & Analogies
Picture blowing up a balloon. When you blow air into a balloon, you create a high-pressure area inside compared to the lower pressure outside. The air flows from the high-pressure area (inside the balloon) to lower-pressure areas (outside). Similarly, in fluids, pressure differentials dictate how the fluid moves.
Understanding Streamline, Pathline, and Streakline
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Streamline is a line everywhere it is a tangent to the velocity vector at a given instant. Pathline is the actual path traversed by a given fluid particle, while Streakline is the locus of particles that have earlier passed through a prescribed point.
Detailed Explanation
This section explains three concepts that help visualize fluid flow—streamline, pathline, and streakline. A streamline shows the direction of flow at an instant, indicating the direction of the velocity vectors. A pathline traces the journey of a specific fluid particle over time. Streaklines visualize the paths of particles that have passed through a specific point, often visualized by dye or color differences in fluid.
Examples & Analogies
Imagine observing a river. The streamline shows where the water flows at one moment, the pathline follows a single leaf floating down the river as it moves, and the streakline shows areas colored by dye introduced at a specific point in the river. Each illustration helps understand fluid motion in different contexts.
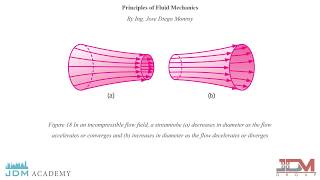
The Role of Stream Tubes in Fluid Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I have drawn the streamlines, and it is occupied a certain space like this the stream tube. In that case is a very simplified case is now the only the flow will be entering from the side and go out from this. Since the streamlines do not allow any flow cross through that as the definitions indicate for us.
Detailed Explanation
A stream tube is a volume of fluid bounded by streamlines. No fluid enters or exits through the boundaries of a streamtube, making it useful for analyzing flow. This property allows fluid mechanics to simplify complex flow patterns into manageable sections, which is essential for solving problems using the conservation of mass and momentum.
Examples & Analogies
Think of a water slide at a playground. As a child slides down, the flow of water alongside them creates a specific path. The water flow is like the streamtube, containing the water that supports them without spilling over the sides, allowing us to analyze the speed and direction of the water effectively.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fluid Mechanics: The study of fluids (liquids and gases) and the forces acting upon them.
-
Velocity Field: The representation of the velocity of fluid particles in fluid dynamics.
-
Pressure Distribution: The variation of pressure throughout a fluid flow region, crucial for understanding how fluids behave.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Visualizing airflow around an airplane wing using dye to create streaklines.
-
Examining the flow patterns in a pipe to determine the optimal design for minimizing resistance.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Streamlines flow in a line, where velocity is the sign.
📖 Fascinating Stories
-
Imagine a race of colored fluid balls navigating a course. Streamlines guide their paths, showing where they'll go without conflict!
🧠 Other Memory Gems
-
Remember 'SPS' for flow visualization: Streamlines, Pathlines, Streaklines.
🎯 Super Acronyms
FPS
- Flow
- Pressure
- Streamlines - the key elements to visualize fluid behavior.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Streamline
Definition:
A line that is everywhere tangent to the velocity vector of the flow at a given instant.
-
Term: Pathline
Definition:
The actual trajectory traced by a fluid particle over time.
-
Term: Streakline
Definition:
The locus of points that have passed through a specific point in a flow.
-
Term: Mass Conservation Equation
Definition:
An equation stating that mass cannot be created or destroyed in an isolated system.
-
Term: Momentum Equation
Definition:
An equation that describes the motion of fluid particles, accounting for forces acting on them.