Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Analyzing Velocity and Pressure Fields
Unlock Audio Lesson
Today, we're going to explore how we can analyze velocity and pressure fields within fluid mechanics, particularly in steady flows. Can anyone explain what a velocity field is?
Is it a representation of how fast something moves in a fluid?
Exactly, Student_1! A velocity field shows how velocity is distributed in space. We represent it using vector quantities: u, v, and w. Can someone tell me what these variables correspond to?
U is for the x-direction, v is for the y-direction, and w is for the z-direction!
Right! Now, let's talk about pressure distribution. Why do you think it's important in fluid flow analysis?
I think it helps us understand where the flow will go based on pressure gradients.
Great point, Student_3! Pressure gradients indeed indicate flow direction. To sum up this session, velocity fields are essential for understanding the fluid's motion, and pressure distribution helps explain how forces act on the fluid.
Incompressible vs. Compressible Flow
Unlock Audio Lesson
Let's move on to incompressible and compressible flows. What is an incompressible flow?
It's when the fluid density remains constant throughout the flow, right?
Correct! And this usually applies when the Mach number is less than 0.3. How about compressible flow? What do we expect there?
The density will change depending on the flow conditions, right?
Exactly! Density variations affect pressure and velocity directly in compressible flows. To verify understanding, why might we neglect density in many fluid problems?
Because if the Mach number is low, the incompressibility assumption simplifies the analysis!
Very well explained, Student_2! To wrap up this session, incompressible flows simplify our analysis due to constant density, while compressible flows require us to consider density variances.
Real-world Applications of Pressure Distribution
Unlock Audio Lesson
Now that we've covered the theory, let’s talk about some real-world applications! Where do we see pressure distribution being vital?
In weather predictions, right? Since air flows affect weather systems?
Correct, Student_3! Weather forecasting models rely heavily on computational fluid dynamics, which depends on analyzing pressure gradients. What about in engineering?
I'd guess in designing airplanes or cars to optimize airflow.
Absolutely! Engineers analyze how pressure influences objects in motion for better design and performance. What can we conclude about the importance of fluid mechanics in these applications?
It’s essential for predicting behavior and optimizing designs in various fields.
Exactly right, Student_1! Let's summarize: pressure distribution plays a critical role in understanding and predicting the behavior of fluids across many real-world applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the analytical solutions for velocity and pressure distribution in incompressible steady flows, highlights experimental approaches, and discusses the significance of pressure gradients in determining flow direction. Key concepts such as velocity fields, pressure distribution dynamics, and the conditions under which fluid flows can be considered incompressible or compressible are also introduced.
Detailed
Pressure Distribution in Fluid Mechanics
This section emphasizes the importance of analyzing pressure distribution within fluid mechanics, specifically in the context of steady, incompressible flows. In such cases, analytical methods are employed to derive equations for velocity (u, v, w) and pressure that adhere to conservation principles, such as mass and linear momentum.
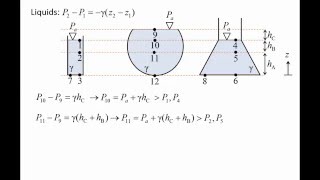
Two examples are explored to illustrate the pressure field and velocity field: 1) wind flow over a weather radar setup and 2) a jet flow impacting on a floor. The concept of the velocity field, represented as a vector quantity, is segmented into scalar components (u, v, w) within a Cartesian coordinate system.
Pressure distribution serves as a dynamic variable essential for understanding fluid flow. The pressure gradient indicates flow direction, while the first law of thermodynamics may be introduced for scenarios with significant heat exchange. Conditions such as density variations in compressible flows contrasted with the constant density in incompressible liquids are articulated.
Ultimately, this section lays the groundwork for resolving fluid flow problems by analyzing pressure and velocity fields.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Analytical Solutions and Conservation Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So for a very simple case, we can get analytical solutions like u and v and w and the pressure, and that analytical solutions can help us to know the velocity, the pressure distribution of these problems and it satisfies conservation equations, mass conservation equations, linear momentum equations. Also it satisfies the boundary conditions at the floor and the flow inject what is coming in.
Detailed Explanation
Analytical solutions in fluid mechanics refer to mathematical equations that describe flow properties such as velocity (u, v, w) and pressure. These solutions are derived using fundamental conservation laws, including the conservation of mass and momentum. In a simple case, such as a two-dimensional incompressible steady flow, the solutions provide insight into how pressure and velocity change spatially and ensure that the physical laws governing fluid dynamics are satisfied. Importantly, boundary conditions—constraints that describe the behavior of fluids at boundaries, such as surfaces—need to be accounted for to obtain meaningful solutions.
Examples & Analogies
Consider the flow of water from a garden hose: if you point it at a wall, the way the water splashes and spreads provides a practical example of pressure and velocity distribution. The hose's opening creates a defined boundary, and observing how water behaves at that boundary (like splashing or spreading) illustrates how analytical solutions apply in real life.
Velocity Field Definition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So now I am just defining the velocity field. When we are talking about, we are talking about this velocity as a vector quantity, which varies in space in case of the Cartesian coordinate system of x, y, z and the time. We resolve this velocity vector component into its scalar component in Cartesian coordinate systems.
Detailed Explanation
A velocity field is a description of how the velocity of a fluid varies in three-dimensional space and over time. In fluid mechanics, it is often represented as a vector field, where each point in space has a velocity described by its components (u, v, w) along the x, y, and z axes respectively. The scalar components of these vector quantities provide specific values of velocity at given coordinates, allowing for detailed analysis of fluid flow characteristics. This forms the basis of further calculations, such as determining the rate of change of fluid velocity and acceleration.
Examples & Analogies
Imagine being at a windy beach. The wind speed varies across different areas of the beach; some areas are very windy, while others are calm. The wind's strength and direction at various points can be expressed as a velocity field, illustrating how fluid (air, in this case) behaves differently across space.
Acceleration and Pressure Gradient
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I know the velocity field, we can compute what the acceleration will be, the rate of change of the velocity gradient. About these derivations we will come to when we have fluid kinematics. We will talk about that, but any flow field conditions we can have a velocity field. This means we know the velocity distributions with respect to space and time.
Detailed Explanation
Acceleration in fluid flow is determined from the velocity field by analyzing how velocity changes over time and space. The velocity gradient—a measure of how velocity varies in a specific direction—helps in understanding fluid acceleration. If we know the velocity at every point in a flow, we can derive the acceleration field from this velocity information, which is crucial for predicting how fluids will behave under various conditions.
Examples & Analogies
Think of a car accelerating on a road. If you know the car's speed at various points along the road, you can predict how quickly it will speed up, slow down, or turn. Similarly, in fluid dynamics, knowing the velocity across different regions allows one to anticipate how the fluid will accelerate in response to forces acting on it.
Importance of Pressure Distribution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So the computing of the pressure and the pressure gradient is a major component in fluid flow problems. Many of the time, the pressure gradients indicate for us which direction the flow will be there. This is the reason we always look at the gradient of the force which drives the flow.
Detailed Explanation
Pressure distribution in a fluid is a vital aspect of understanding fluid dynamics, as it dictates how and where a fluid flows based on pressure gradients. A pressure gradient occurs when there is a difference in pressure across a distance. Fluids tend to flow from areas of high pressure to low pressure, so understanding these gradients allows engineers and scientists to predict flow patterns effectively. The relationship between pressure and flow direction is essential for designing various systems, from pipelines to aircraft.
Examples & Analogies
Consider a hiker at the top of a hill: the steepness of the slope indicates the direction they will move. In fluid dynamics, pressure gradients function similarly; higher pressure can push fluid in the direction of lower pressure, much like gravity pulls the hiker down the hill.
Density Implications in Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Second point I am to discuss is the density of the flow. You know it is mass per unit volume or it indicates the mass of the fluid and that what per unit volume we quantified. So if you multiply the volume, you know this is the amount of mass is there.
Detailed Explanation
Density is a critical property of fluids, defined as the mass per unit volume. It plays a major role in fluid dynamics since it affects buoyancy, pressure, and flow behavior. In incompressible flows (typically for liquids), density remains relatively constant. However, in compressible flows (usually for gases), density can change significantly with pressure and temperature. This understanding helps in analyzing various flow conditions and is fundamental in various calculations within fluid mechanics.
Examples & Analogies
Think about how an ice cube floats in a glass of water. The ice cube is less dense than water, which is why it floats. Similarly, understanding density helps predict whether a fluid (like oil or gasoline) will float or sink when mixed with water.
Streamline, Pathline, and Streakline
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So define these flow patterns, we define technically three lines. One is the streamline, pathline, and streakline. Let us look at the definitions.
Detailed Explanation
In fluid mechanics, streamlines, pathlines, and streaklines are three key ways to visualize fluid flow. A streamline represents the path a fluid element would follow at a specified moment in time and is tangent to the velocity vector. Pathlines trace the actual path of a fluid particle over time, showing where it travels as time progresses. Streaklines connect all the points that have passed through a specified point in space at different times. Understanding these concepts is essential for analyzing flow characteristics and predicting the behavior of fluids in motion.
Examples & Analogies
Imagine watching a water fountain. The streamlines would show the shape of the water flow at a single moment, the pathlines would represent the actual trajectories of individual water droplets over time, and the streakline might appear as a colorful spray of water captured during a show, linking all the drops that have passed through the same spot.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Velocity Field: A representation of fluid motion, decomposed into u, v, and w components.
-
Pressure Distribution: Influences fluid dynamics by dictating flow direction based on pressure gradients.
-
Incompressibility: Assuming constant density simplifies fluid flow analysis when the Mach number is low.
-
Compressibility: Density variations must be considered in flows with high Mach numbers.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A weather radar setup observing wind flow illustrates pressure distribution affected by speed.
-
A jet flow impacting on a flat surface showcases interactions between velocity and pressure fields.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Pressure can measure, it guides the endeavor, in flow’s gentle tether, it moves all together.
📖 Fascinating Stories
-
Imagine a hero riding a stream of water; their path changes with pressure highs and lows, guiding their adventure.
🧠 Other Memory Gems
-
Use 'PV-m' to recall: 'P' is for Pressure, 'V' for Velocity; 'm' for the relationship among them in flows.
🎯 Super Acronyms
Remember 'I-C' for Incompressible and Compressible flows; 'I' means constant, 'C' means change.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Velocity Field
Definition:
A vector representation that shows how the velocity of a fluid varies in space.
-
Term: Pressure Gradient
Definition:
The rate of pressure change in a fluid flow that affects the flow direction.
-
Term: Incompressible Flow
Definition:
A flow where the fluid density remains constant throughout the motion.
-
Term: Compressible Flow
Definition:
A flow in which the fluid density changes significantly depending on the flow conditions.
-
Term: Mach Number
Definition:
A dimensionless quantity representing the ratio of the speed of an object to the speed of sound in the surrounding medium.