Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Incompressible Flow
Unlock Audio Lesson
Today, we're discussing incompressible flow. Does anyone know what Mach number signifies in fluid flow?
It measures the speed of the flow relative to the speed of sound, right?
Exactly! When we say the Mach number is less than 0.3, it means we're in an incompressible flow regime. Can anyone tell me what that implies for density?
Density remains constant, so we can simplify our calculations.
Correct! A mnemonic to remember this is 'IMPACT' - Incompressible Means PConstant and Accurate Timing. This helps us remember that for low Mach numbers, we can assume constant density.
So, if we treat density as constant, what type of equations do we use?
We use the mass conservation equations, which relate mass inflow to outflow. Let's summarize: Assumption of incompressibility allows simplification in our equations.
Mass Conservation Derived from Momentum Transport
Unlock Audio Lesson
Next, let’s discuss how the Reynolds transport theorem applies to our equations. Anyone familiar with that theorem?
I think it deals with how mass changes in moving control volumes, right?
Spot on! It helps us express how mass enters and exits a control volume. Why do you think this is significant in fluid dynamics?
It helps us account for all mass changes over time.
Exactly! Without this, we wouldn’t accurately describe dynamic systems. As we apply these concepts, remember this rhyme: 'Reynolds rule for mass flow – entry or exit, go with the flow.' This idea emphasizes maintaining control.
So, it’s all about keeping track of mass within the volume?
Yes! Let’s summarize: The Reynolds transport theorem enables us to accurately track mass changes across control volumes.
Velocity Field and Flow Conditions
Unlock Audio Lesson
Now onto the role of velocity fields. How do you think velocity impacts mass conservation?
Well, different velocities can affect the rate of mass inflow and outflow, right?
Exactly! An average velocity is often used but remember 'A for Average, in control phase.' This means assessing your velocity accurately is crucial in flow calculations.
What if the velocity isn't constant?
Great question! You may need to conduct surface integrals to find an average. To summarize: Understanding average velocities and their distributions is essential for flow applications.
Practical Applications of Mass Conservation
Unlock Audio Lesson
Let’s explore some real-world applications now. Can anyone provide an example where mass conservation applies?
Maybe in tanks when calculating water height changes?
Spot on! We often analyze flow in tanks, like assessing water height change with two inlets. Remember our last example: 'Two in, one out, water height's clout.' Can someone explain how it works?
We compare inflows and outflows, then apply mass conservation to get the height change.
Exactly! This illustrates how theoretical concepts directly influence engineering design. Let’s summarize: Applying mass conservation in practical problems illustrates its significance.
Seepage Rates in Engineering
Unlock Audio Lesson
Lastly, let’s discuss seepage. How is seepage related to mass conservation?
It’s about understanding how much water leaves a control volume.
Exactly, and we can calculate seepage using the conservation principle in systems like rivers. 'Seepage flows free, control the decree!' can help you remember how to manage flow systems.
Can this apply to groundwater studies?
Absolutely! Groundwater flow and river interactions are prime examples. Let's summarize: Seepage rates are derived from mass conservation and are vital in environmental engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on the mass conservation equation's application in incompressible flows, explaining how densities remain relatively constant under certain conditions and how this allows for simplifications in calculations. It further clarifies the different approaches taken based on flow conditions and provides practical examples of how these concepts are implemented in real-world scenarios.
Detailed
Application of Mass Conservation Equation
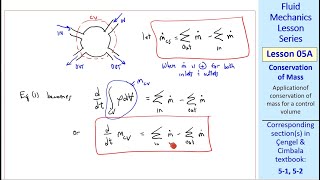
The mass conservation equation is a fundamental principle in fluid mechanics that asserts that the mass of a fluid remains constant in a closed system over time. This principle finds practical application in various flow problems, particularly when analyzing incompressible flows.
Key Points
- Incompressible Flow Assumption: When the flow's Mach number is less than 0.3, we can assume the flow is incompressible, meaning that density variations are negligible. This greatly simplifies the calculations, allowing us to treat density as a constant.
- Flow Equations: For volumetric flux calculations in incompressible flow, we can derive key equations relating velocity and area, concluding that mass flux will equal the inflow and outflow rates when density remains constant.
- Application of Control Volume: The Reynolds transport theorem is introduced as a means of deriving flow equations within defined control volumes, indicating how mass within the system changes as inflows and outflows occur.
- Velocity Field Knowledge: Understanding the velocity fields is essential; whether the flow is steady or unsteady affects the mass conservation equations significantly. This includes estimating inflow and outflow based on average velocities across the control surfaces.
- Practical Examples: The section illustrates these concepts with practical problems, such as calculating changes in water height in a tank and determining seepage rates in river systems, thereby applying theoretical principles to real-world engineering challenges.
In summary, the conservation of mass is foundational for analyzing fluid systems, requiring a careful assessment of flow conditions and velocity fields for accurate application.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Incompressible Flow Simplification
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let me come in to the, if the flow is incompressible. Again, we have a lot of simplifications. Again, I can repeat it. The flow systems when you have mac number less than 0.3, okay, whether it is gas, whether it is a liquid or any flow system, if you think that the within the flow system the flow becomes less than the mac number less than 0.3, then there will be density variation, but that variation of density is much much negligible comparing to other components.
Detailed Explanation
The concept of incompressible flow arises when the Mach number (a measure of speed relative to the speed of sound) is less than 0.3. At this low Mach number, density variations in the fluid are so slight that they can be ignored. Consequently, we treat the fluid as incompressible, meaning that density remains constant throughout the flow. This simplification greatly simplifies our calculations and analyses in fluid mechanics.
Examples & Analogies
Think of a water pipe. When water flows through it at a slow speed, changes in the water's density are negligible, much like how a baseball doesn't change size as it moves through the air at slow speeds.
Mass Flux and Volumetric Flux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, there, the scalar product of V and n and d A, okay, and density can come out. So, instead of the mass flux we are now talking about volumetric flux. That means, if you multiply the velocity into area, then what you get is unit volume per unit height, volumetric flux, okay?
Detailed Explanation
In fluid mechanics, mass flux refers to the mass of fluid passing through a unit area per unit time, while volumetric flux refers to the volume of fluid passing through a unit area per unit time. When we ignore density changes in incompressible flow, we can use volumetric flow rate, which simplifies our calculations: Q = A × V, where Q is the discharge, A is the cross-sectional area, and V is the average velocity.
Examples & Analogies
Imagine a garden hose. The amount of water that flows out per second depends on the cross-sectional area of the hose and how fast the water is pushed through. Similarly, knowing the area of a pipe and the flow rate helps us understand how much water moves through it.
Understanding Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, to solve this mass conservation equation I should have knowledge on velocity field. I should know how the velocity varies or I should know whether the velocity is a constant or the velocity varies.
Detailed Explanation
A control volume is a defined space through which fluid flows, helping us analyze mass flow in and out of that space. Understanding how velocity changes at different points within that volume is key to applying the mass conservation equation. If we know how fast fluid is moving and in what direction, we can calculate the mass entering and leaving the control volume, allowing us to determine the overall change in mass within the volume.
Examples & Analogies
Imagine a classroom filled with students. If you know the entrance (where students come in) and exit (where students leave) and can monitor how many students walk in and out over time, you can calculate how many students are in the classroom at any given moment.
Velocity Field Considerations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, basically, when you apply the mass conservation equation your knowledge of velocity variation is important to you, how you are simplifying the velocity field on the control surface.
Detailed Explanation
When applying the mass conservation equation, understanding how velocity changes across the control surface is crucial. If velocity is constant, the calculations simplify considerably. In real-world problems, however, velocity often varies, which requires a more nuanced approach, potentially involving integration to account for these variations.
Examples & Analogies
Think of a river with varying speeds. In some areas, the water flows quickly, while in others, it flows slowly. Understanding these changes helps us estimate how much water is moving downstream at any point.
Flow Classification and Control Volume Application
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Whenever you solve the problem, you classify the problem. Once you classify problems it gives indirectly that these are the assumptions that are valid for this problem that we are solving.
Detailed Explanation
Classifying the flow helps establish the assumptions we can safely make. Are we dealing with laminar or turbulent flow? Is the flow steady or unsteady? These classifications dictate how we apply the mass conservation equation and select the appropriate control volume, simplifying our calculations while ensuring accuracy.
Examples & Analogies
Consider a chef preparing different dishes. Each dish might need a different cooking method (stir-frying, boiling, baking) based on its ingredients (vegetables, meat, desserts). Similarly, classifying fluid flow helps us determine the best method to analyze it.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Conservation: Fluid mass is conserved in flow systems.
-
Incompressibility: Density remains constant for low Mach number flows.
-
Reynolds Transport Theorem: Connects changes within a control volume to flow across its boundary.
-
Velocity Variation Importance: Knowledge of velocity distribution is crucial for applying mass conservation.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of calculating change in water height in a tank with two inflows.
-
Example of determining seepage rates in rivers using mass conservation principles.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Incompressible fluid, it won't change, density's a constant, that’s the game.
📖 Fascinating Stories
-
Imagine a pond filled to the brim; as the rain pours, the level begins to swim. Water flows in but stays the same, with changes unmade, keeping the balance is the aim.
🧠 Other Memory Gems
-
'Incompressible Flow = Density Constant' helps remember that during low-speed motion.
🎯 Super Acronyms
RMT - Reynolds Mass Transport
- Remember the equation connects mass movement across boundaries.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Conservation Equation
Definition:
An equation that states that mass cannot be created or destroyed in a closed system; it is conserved over time.
-
Term: Incompressible Flow
Definition:
Flow where the density of the fluid remains constant; applicable when the Mach number is less than 0.3.
-
Term: Mach Number
Definition:
A dimensionless number representing the ratio of fluid velocity to the speed of sound in that medium.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that establishes a relationship between the rate of change of mass in a control volume and the flow of mass across its boundaries.
-
Term: Control Volume
Definition:
A defined volume in space through which fluid flows, used for analysis in fluid mechanics.
-
Term: Velocity Field
Definition:
A representation of the velocity of fluid particles in space, indicating how velocity varies across the flow.