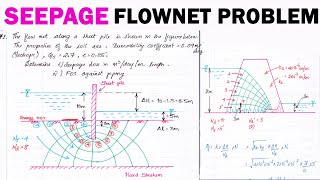
Seepage Problem in a Flume
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Incompressible Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will discuss incompressible flow. What do you think it means when we say flow is incompressible?

I think it means that the density of the fluid doesn't change.

Exactly! When the Mach number is below 0.3, we can assume that density remains constant. This simplifies our equations significantly.

Why is the Mach number important?

Great question! The Mach number helps us understand the speed of the flow relative to the speed of sound. At low speeds, density changes are negligible. Keep that in mind as it leads to important conclusions about flow characteristics.

Remember, the acronym *ICF* can help you remember Incompressible Flow: Invariant density, Continued flow.

So, ICF will help us remember that density is constant in incompressible flow?

That's right! Now, let’s summarize: an incompressible flow is characterized by a Mach number less than 0.3, which means we can treat density as constant.
Understanding Mass Conservation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we understand incompressible flow, let’s dive into mass conservation. What does this principle state?

That mass cannot be created or destroyed in a closed system?

Exactly! When we apply this to fluid mechanics, we are often looking at the inflow and outflow of mass. Can anyone give me the central equation we use?

Is it the mass flow rate equations involving density and velocity?

Right. When we know that density is constant, we can derive the volumetric flow, which simplifies our calculations. What's the equation for volumetric flow, again?

Q = A * V, where A is the area and V is the velocity.

Perfect! Here’s a memory aid: *VAM*, which stands for Velocity times Area equals Mass flow. Always remember this to aid your problem-solving!

So, if we apply this in our seepage scenarios, we must carefully consider our inflow and outflow areas?

Yes! To summarize today’s lesson: mass conservation helps in analyzing flow by considering inflow against outflow. We know that the conservation equation emphasizes the balance in a control volume.
Velocity Distribution in Flumes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let's talk about velocity distribution. Why is it important in fluid dynamics?

Because it can affect how we calculate discharge and seepage?

Precisely! Within a pipe or flume, velocity isn't uniform; it varies based on position. Who can tell me about the velocity profile near the walls?

The velocity is zero at the walls and maximum at the center?

Yes! This distribution is crucial for integrating and calculating average velocities. What’s the formula we often use for average velocity?

V_avg = ∫V dA / A?

Exactly! And remember the acronym *ACE*, for Area Contribution Evaluation – as we evaluate average velocity based on the cross-sectional area.

So, we have to focus on the velocity profile when assessing inflow and outflow in our seepage calculations?

Correct! To summarize, understanding velocity distributions is key to applying mass conservation effectively in various fluid problems.
Real-World Applications: Seepage Calculation Example
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's look at a practical example of seepage in a flume. Can anyone explain how we calculate seepage rates?

We need the velocity at the upstream and downstream, along with the width and depth of the channel?

Correct! We use the average velocities and the dimensions to find the flow rates. Anyone remember the formula we discussed?

It's Q = B * H * (V1 - V2).

Well done! Now, how would you apply values from a given problem into this formula?

You would substitute the known width, depth, and velocities into the equations to calculate specific seepage?

Exactly! As a memory aid, think *SDW* for Seepage Discharge Width. It captures the essence of how seepage is related to flume dimensions.

So, understanding these calculations lets us assess environmental impacts or water management strategies?

Absolutely! In summary, applying our understanding of flow and seepage calculations allows us to address real-world hydraulic issues effectively.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section elaborates on situations where fluid flow is considered incompressible, particularly when the Mach number is less than 0.3. It also explains the concept of volumetric flux, mass conservation equations, and the significance of understanding velocity variations in solving flow problems, including practical examples of seepage in a flume.
Detailed
Incompressible Flow and Mass Conservation
The section begins by outlining the conditions under which fluid flow can be approximated as incompressible, particularly when the Mach number is less than 0.3. In such cases, density variations are negligible, simplifying the conservation of mass equations.
Key Equations
The central equation described is the mass conservation equation where the term for density can be extracted due to its constancy.
Concept of Volumetric Flux
The discussions shift towards volumetric flux, where velocity multiplied by cross-sectional area gives the flow rate without directly involving density, which is assumed to be constant.
Velocity Field Understanding
A significant emphasis is placed on understanding how the velocity varies across a control volume. The need for assessing the velocity field accurately is highlighted, as it directly impacts the application of mass conservation principles.
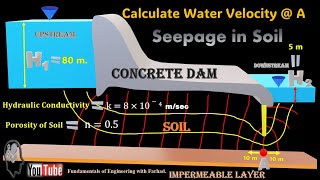
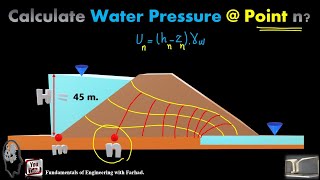
Throughout the section, various applications involving seepage rates from experimental flumes are introduced. For instance, calculations of water inflow and seepage rates at a flume utilizing upstream and downstream velocities are showcased, emphasizing the real-world application of the discussed concepts. This leads to several problems involving different control volumes, providing a practical grounding of the theoretical principles covered.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Incompressible Flow and Density Assumptions
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, let me come in to the, if the flow is incompressible. Again, we have a lot of simplifications. Again, I can repeat it. The flow systems when you have mac number less than 0.3, okay, whether it is gas, whether it is a liquid or any flow system, if you think that the within the flow system the flow becomes less than the mac number less than 0.3, then there will be density variation, but that variation of density is much much negligible comparing to other components.
So, we can assume the flow is incompressible nature. Again, I am going to summarise that. When you have any flow systems, mac number is less than 0.3, so we can use flow as incomprehensible flow, density does not vary significantly. So, density becomes constant, as density becomes constant, as you know it, it is very simplified problem what we are going to solve.
Detailed Explanation
In fluid mechanics, flow can be categorized based on the Mach number, which is a dimensionless number used to represent the speed of an object moving through fluid to the speed of sound in that fluid. Here, when the Mach number is less than 0.3, it indicates that the flow is incompressible, meaning that changes in pressure or speed have little effect on the fluid's density. Therefore, for low-speed flows, density can be treated as a constant, simplifying the analysis and calculation of fluid parameters.
Examples & Analogies
Think of a water pipe in a household setting. When you open a faucet very slightly, the flow is slow, and the density of water remains effectively constant, enabling us to predict how much water will flow out. However, if the pipe were to carry gas at high speeds (high Mach number), the behavior would change, as density variations significantly impact the flow.
Mass Conservation Simplification
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, density varies negligible, as the density variation is not significant and beta equal to 1, so only this equation is left for us. Simple thing. This is very simple equation. DB sys = ρ ∗ VdA + ρb(V ⋅ n) dA
Detailed Explanation
Here, we are discussing the simplification of mass conservation equations under the assumption of incompressible flow. Since density is assumed constant across the system, we can express the mass flow using volumetric flow rates instead of mass flow, which simplifies our calculations. The equation presented relates the change in mass within a control volume to the incoming and outgoing flow rates, with terms representing area and velocity.
Examples & Analogies
Imagine filling a bathtub: the water flows in through the tap (influx) and may drain out through the overflow (outflux). If we know the tap’s flow rate, how much water is entering versus leaving becomes straightforward because we assume the density of water is constant as it fills, allowing us to focus on the volumetric flow rates.
Viscous Flow and Velocity Distribution
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If the inlet and outlet are one-dimensional, Q = A * V. Only that we are not showing the density multiplication. If you multiply with a Q, the V into A is Q is discharge. So, Q = V * A, is the discharge.
Detailed Explanation
This section covers how to calculate the discharge (Q) in a fluid system, defined as the volumetric flow rate through a specific cross-sectional area (A) multiplied by the velocity (V) of the fluid. Even though density is not explicitly mentioned, it's understood that since this analysis is under incompressible flow, density is implicitly accounted for. It’s important because it connects the flow dynamics with the control volume concept ensuring that we maintain mass balance.
Examples & Analogies
Consider a garden hose: when you turn on the water, it flows out of a nozzle. If you know the nozzle's diameter (A) and the speed of the water (V), you can easily calculate how much water comes out of the hose per second. If you open the nozzle fully, the discharge also increases, illustrating the relationship between area, velocity, and discharge.
Analyzing Seepage in a Flume
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The water is flowing in a flume with a downward seepage average velocity at upstream is 0.3 m/s and at downstream is 0.26 m/s. the width and depth of the channel are 1m and 0.15m respectively. Find out the quantity of seepage (q).
Detailed Explanation
This problem specifically focuses on a flume, which is a narrow channel designed to direct water flow. By knowing the average velocities at both upstream and downstream, as well as the channel's dimensions, we can calculate the seepage rate, which is the rate at which water flows vertically downward into the ground. We'll derive the seepage from the difference in flow rates multiplied by the channel dimensions, applying the principle of mass conservation.
Examples & Analogies
Imagine a drainage ditch where rainwater collects. As water collects, some of it seeps into the ground. If we know how fast the water is flowing through the ditch and the dimensions of the ditch, we can estimate how much water is being absorbed into the ground, similar to measuring how much rainwater gets absorbed by a garden bed.
Solving the Seepage Problem
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Applying the control volume approach, equation for the steady flow
0 = ρ1A1V1 - ρ2A2V2 + q. This is the outflux going out from this. This is outflow, seepage, downward path. So, if you rearrange it, you can get the value of q as seepage rate.
Detailed Explanation
The equation presented applies mass conservation principles to evaluate the seepage from the flume. By equating the inflow mass to the outflow along with the seepage rate, we can isolate q. Essentially, we determine how much mass is lost to seepage over time per unit length of the flume. It’s crucial for optimizing water management and understanding flood dynamics.
Examples & Analogies
Think about how a sponge works. If you pour water onto a sponge, it absorbs moisture (seepage) depending on how quickly the sponge soaks and the thickness of the sponge. Understanding this allows scientists to predict how water interacts with soil and drainage systems in farming or landscaping.
Key Concepts
-
Incompressible Flow: Characterized by constant density; relevant for flows with a Mach number below 0.3.
-
Mass Conservation Principle: States that mass inflow equals mass outflow within a control volume.
-
Volumetric Flow Rate: Calculated by multiplying cross-sectional area by flow velocity, crucial for analyzing fluid systems.
-
Velocity Distribution: Variation of velocity across a flow cross-section affects calculations of discharge and seepage.
Examples & Applications
Example 1: Calculating the volumetric flow rate in a flume given upstream and downstream velocities, and dimensions.
Example 2: Assessing how changes in velocity distribution affect seepage rates in hydraulic systems.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Incompressible flow, where density is low; Mach under 0.3, make sure you know!
Stories
Imagine a calm river where water flows smoothly, always steady, never changing its form, just like density in incompressible flow.
Memory Tools
Remember ICF for Incompressible Fluid – Constant Density.
Acronyms
Use *VAM* for 'Velocity times Area is Mass flow'.
Flash Cards
Glossary
- Incompressible Flow
Flow in which density variations are negligible, allowing the treatment of fluid density as a constant.
- Mach Number
A dimensionless quantity representing the ratio of the speed of fluid to the speed of sound in that fluid.
- Volumetric Flow Rate
The volume of fluid flowing through a cross-section per unit time, computed as Q = A * V.
- Mass Conservation Equation
An equation that states mass flow into a control volume equals mass flow out, under steady state conditions.
- Velocity Distribution
The variation of flow velocity across a cross-section, greatly influencing flow behavior and calculations.
Reference links
Supplementary resources to enhance your learning experience.
