Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Incompressible Flow
Unlock Audio Lesson
Today, we'll explore the concept of incompressible flow. When the Mach number is less than 0.3, we can assume that density variations in the flow are negligible. Can anyone tell me why this assumption is important?
It's important because it simplifies our equations and calculations.
Exactly! When we treat the flow as incompressible, we use simpler equations, making our models easier to manage. Does everyone remember the Reynolds transport theorem?
Yes! It helps us relate the mass flow into and out of a system.
Right. By applying it, we can analyze mass flows with reasonable ease.
To summarize, assuming incompressible flow simplifies our work as density changes can be negligible under certain conditions.
Mass Conservation Equations
Unlock Audio Lesson
Let's dive into mass conservation equations. Can someone explain what we generally include in these equations?
We include inflows and outflows, and we calculate the change in storage.
Correct! The influx should equal the outflow plus any change in storage. This tells us how mass moves through our control volume.
So, if we know the inflows and outflows, we can find changes in storage?
Exactly! It's all about understanding how fluids interact within their environments.
In short, mass conservation equations help us predict how much fluid is retained in a system.
Practical Applications in Soil Matrix Problems
Unlock Audio Lesson
Let's consider the soil matrix problem. How does percolation affect water storage in soils?
Percolation shows how water moves through soil and can affect how much water is stored there.
Correct! When there’s a downward flow, we must apply our equations considering this storage and the hydraulic conductivity. Can anyone pinpoint what hydraulic conductivity refers to?
It relates to how easily water can move through the soil.
Exactly! Understanding hydraulic conductivity is vital for calculating percolation rates.
In conclusion, soil percolation plays a crucial role in hydrology and understanding fluid dynamics in soils.
Example Problem: Tank Filling with Water
Unlock Audio Lesson
Let’s apply our knowledge to a real problem. We have a tank being filled with water. Who can outline the steps we might take to classify and solve this problem?
We start by identifying it as unsteady flow since the water level is changing over time.
Great start! What's next?
Next, we would determine the input flow rates and any effects from air trapped at the top.
Exactly! Since we have inflow but no outflow, we focus on mass changes in the tank. This type of analysis is vital in real-world applications, too.
Remember, class, always classify your problems carefully before proceeding with calculations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the significance of incompressible flow in fluid mechanics, outlining how variations in density can be neglected under certain conditions. It further discusses practical applications, including a detailed problem involving percolation within a soil matrix, emphasizing the importance of correctly classifying fluid flow and understanding the velocity field.
Detailed
Detailed Summary
This section addresses key concepts in fluid mechanics, emphasizing mass conservation in incompressible flow systems. When the Mach number is less than 0.3, density variations are negligible, allowing for simpler equations where density can be considered constant. The section covers the flow equations derived from the Reynolds transport theorem and stresses the importance of the velocity field when applying mass conservation equations.
Key problems illustrate these concepts, such as a tank being filled with water with an air valve allowing for air expansion and an intricate case of seepage flow from a soil matrix, which depends on the storage within the system. By applying Reynolds transport theorem, the relationship between inflows, outflows, and percolation can be established, solidifying the connections between theoretical principles and practical applications in fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
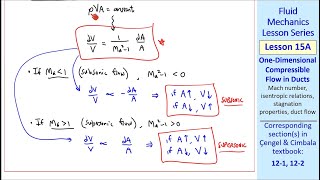
Understanding Incompressible Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The flow systems when you have mac number less than 0.3...we can assume the flow is incompressible nature.
Detailed Explanation
In fluid dynamics, the Mach number (Mac) is a ratio that compares the speed of a fluid to the speed of sound in the fluid. When the Mach number is less than 0.3 (i.e., Mac < 0.3), it indicates that flow can generally be treated as incompressible. This means that the density of the fluid remains nearly constant. Hence, any minor variations in density resulting from changes in pressure are considered negligible in the context of simplifying the equations governing fluid flow.
Examples & Analogies
Think of a slow-moving car (representing the fluid flow) driving in traffic. As it moves slowly, the air around it isn’t significantly disturbed — you can consider it steady air (incompressible) surrounding the car. If the car were speeding (high Mac number), it would compress the surrounding air, creating turbulence and pressure changes. Similarly, under slow-flowing conditions, density impacts on the fluid are minimal.
Flow Equations and Mass Flux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Instead of the mass flux we are now talking about volumetric flux... volumetric form has come in because you have taken out the density.
Detailed Explanation
Mass flux is a measure of the mass of fluid passing through a given area per unit time. When considering incompressible flow, if the density is constant, we shift our focus to volumetric flux, which quantifies the volume of fluid flowing through an area per unit time. This step simplifies calculations, making it easier to use the continuity equation — which states that mass inflow must equal mass outflow — leading to simpler relationships like Q = A × V, where Q is volumetric flow rate, A is the cross-sectional area, and V is the velocity.
Examples & Analogies
Imagine watering a garden with a hose. When you turn the nozzle (adjusting the flow), the amount of water that flows out (volumetric flow rate) is dependent on both the size of the opening (area) and how fast you move the nozzle (velocity). If the density of the water were to change significantly, imagine how trickier it would be to maintain the right amount of water flow, similar to adjusting air pressure when inflating a tire.
Velocity Distributions in Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If this is simple in and out system, you can know this velocity distribution area...To solve this mass conservation equation I should have knowledge on velocity field.
Detailed Explanation
In fluid flow, particularly within pipes, velocity is not uniform across the cross-section; it often varies, being higher in the center and lower near the edges due to friction with the pipe walls. Understanding this distribution is essential for solving mass conservation equations. By studying how the velocity changes across the flow area, we can accurately calculate parameters such as discharge and flux, which are essential for engineering applications.
Examples & Analogies
Picture a river with a fast current in the middle. As you move closer to the banks, the water slows down due to friction with the riverbanks. If you're trying to measure how much water flows past a certain point in the river over time, you need to account for the fact that the water in the center is moving faster than the water near the sides.
Average Velocity Computation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The average velocity what we get...represents average velocity.
Detailed Explanation
Average velocity is used when analyzing flow across various conditions. It is calculated by considering the velocity distributions and finding an average across the entire area of interest. This average, when multiplied by the area, gives you a measure of discharge. In scenarios where the velocities vary, average calculations help simplify complex distributions into manageable figures for practical application.
Examples & Analogies
Think of average velocity like calculating the average speed of a road trip. Some stretches of the road may be faster due to being straight and clear, while others may be slower due to traffic or sharp turns. The overall average speed gives you a sense of your travel pace without needing to account for every little variation.
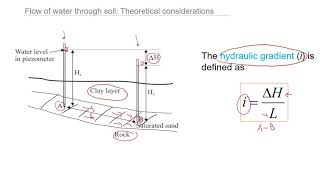
Understanding Percolation in Soil Matrix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The soil matrix is filled with water by the two one-dimensional inlets...where S is storage and K is hydraulic conductivity.
Detailed Explanation
The soil matrix involves complex interactions between water flow and soil properties. Percolation refers to the movement of water through soil, and it is influenced by the soil’s hydraulic conductivity (K), which is a measure of how easily water can move through the soil's pores. The equation Q = f(S) = KS + 0.1 represents the relationship where water flow (Q) depends on the amount of storage (S) in the soil. As more water is stored, the rate of percolation can change, causing these dynamics to be crucial in environmental and civil engineering contexts.
Examples & Analogies
Think of a sponge soaking up water. Initially, it absorbs a lot quickly as it dries out, but as it gets saturated, it becomes harder for water to enter and it starts oozing out. The speed at which the sponge absorbs water resembles the soil matrix's storage and hydraulic dynamics — understanding this helps manage irrigation systems more effectively.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Conservation: The principle that mass must be conserved in fluid dynamics, applying the continuity equation to analyze flows.
-
Incompressible Flow: A flow where density remains constant, simplifying many fluid equations under certain conditions.
-
Velocity Field: A description of how fluid velocity varies across a given area, crucial for understanding flow behavior.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of a tank being filled with water, where air trapped at the top needs to be considered in the analysis.
-
A seepage case where the percolation of water through soil is connected to the storage capacity and the rate of flow.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Incompressible flows, take it slow, density stays constant, let it flow!
📖 Fascinating Stories
-
Imagine a tank filling up with water where air bubbles rise. Each time you fill it, air escapes, and the tank's height changes—like your sponge soaking up rain.
🧠 Other Memory Gems
-
Remember 'PIVOT' for flow analysis: Percolation, Inflows, Velocity, Outflows, Time.
🎯 Super Acronyms
SIMPLE - Storage, Inflows, Mass conservation, Percolation, Limitations, Equations
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Incompressible Flow
Definition:
A flow condition where the density of the fluid is assumed to remain constant due to low velocity (Mach number less than 0.3).
-
Term: Reynolds Transport Theorem
Definition:
A fundamental principle in fluid dynamics that relates the change in mass within a system to the mass flux across the system's boundaries.
-
Term: Hydraulic Conductivity
Definition:
A measure of a soil's ability to transmit water, dependent on the soil's properties.
-
Term: Percolation
Definition:
The process of fluid moving through a porous substance, such as soil, which can affect storage capacity.