Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Basic Understanding of Mass Conservation at River Confluences
Unlock Audio Lesson
Today, we are going to learn about the mass conservation principle at river confluences, such as the Ganga and Brahmaputra. Can anyone explain what mass conservation means?
I think it means that the mass flowing into a system must equal the mass flowing out, right?
Exactly! This principle is fundamental in understanding how rivers interact. When we look at confluences, we need to calculate the inflows and outflows. For example, how do you think we would calculate the flow rates?
We could use the formula Q = Width times Depth times Velocity?
Yes! That's the equation we will use. Remember the acronym WDV—Width, Depth, Velocity—to help you recall the key components.
What happens if the inflows are greater than the outflow?
Great question! Then we would have an increase in storage in the river system. Now, let's summarize: mass conservation means inflow equals outflow, and we calculate flow with WDV. Ready for more details?
Application of Reynolds Transport Theorem
Unlock Audio Lesson
Now let’s apply the Reynolds Transport Theorem to our confluence problem. Why is this theorem vital in fluid mechanics?
I think it helps us relate quantities in a control volume to those flowing across its boundaries.
That's right! It allows us to derive relationships we can use to determine how storage changes when inflows occur. Let's set up our control volume for the Ganga and Brahmaputra.
What should we define as our control volume here?
Good question! We'll consider the area where these two rivers meet and where the water flows into the Padma River. This control volume will help us track inflows and outflows.
How do we simplify the calculations?
By assuming constant density for incompressible flows and using average parameters for velocity. Remember, simplifying correctly is key! Let's review: we define control volume, apply Reynolds theorem, and keep our calculations focused.
Calculating Flow Rates and Changes in Storage
Unlock Audio Lesson
Let's apply our knowledge to the Ganga-Brahmaputra confluence problem. First, what are the given parameters?
We have widths, depths, and average velocities for both rivers.
Correct! So, how do we calculate the flow for each river?
By using the WDV formula for each river.
Exactly! Once we have Q for Ganga and Brahmaputra, what’s our next step?
We compare those to the outflow for the Padma River to find the change in storage!
Great summary! The change in storage, whether positive or negative, shows how much water is being lost or gained in Padma after the confluence.
Interpreting Results and Real-world Implications
Unlock Audio Lesson
Having calculated the flow rates, why is it important to interpret these results?
To understand how water balance affects the local ecosystem.
Right! The health of the river system depends on the balance of inflows and outflows. If inflow is consistently less than outflow, what might happen?
There could be a risk of drought or ecological damage due to lower levels of water.
Precisely! This is why hydrologists monitor such confluences. In summary, understanding flow rates is essential for managing water resources and flood prevention strategies.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
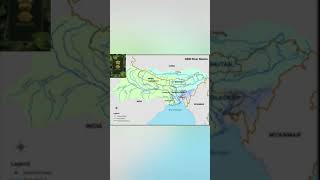
In this section, we analyze the Ganga-Brahmaputra confluence, emphasizing the application of mass conservation laws to determine the storage loss in the Padma River due to inflows from both Ganga and Brahmaputra. Key concepts include calculating inflow and outflow rates, understanding control volumes, and deriving changes in storage.
Detailed
Detailed Summary
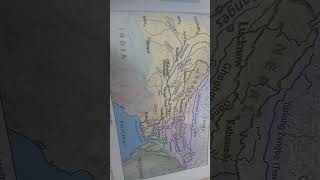
This section focuses on the Ganga-Brahmaputra confluence, where the Ganga and Brahmaputra rivers merge to form the Padma River. We begin by establishing a control volume to examine mass inflows and outflows, applying the principle of mass conservation. The confluence is considered dynamic, hence classified as unsteady and turbulent.
Key Calculations
Given the river parameters:
- Ganga: Width = 700 m, Depth = 1.5 m, Average Velocity = 0.9 m/s
- Brahmaputra: Width = 900 m, Depth = 1.2 m, Average Velocity = 1 m/s
- Padma: Width = 1000 m, Depth = 1.6 m, Average Velocity = 1.2 m/s
We calculate the flow rates using the equation:
$$ Q = Width \times Depth \times Velocity $$
For Ganga and Brahmaputra, we find the respective inflows, followed by calculating the outflow for Padma. By comparing these outputs, we determine the change in storage at the confluence.
Significance
Understanding the mass flow dynamics at such confluences is crucial for environmental management, predicting flood risks, and assessing ecological impacts. The application of the Reynolds Transport Theorem facilitates the transition from volumetric to mass flow metrics, culminating in a clear understanding of water balance in interconnected water systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Confluence Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let us come to the very interesting problem which is there in text book of F.M. White book. What is there, there is a tank. If you look at this figure, there is a tank, two inflows are there, the tank is being filled with waters.
Detailed Explanation
This segment introduces a specific problem involving the flow of water in a tank that receives inflows from two sources. It helps the reader understand the setup before addressing the calculations and flow dynamics involved in a real-world engineering problem where two rivers confluence, particularly focusing on the Ganga and Brahmaputra rivers.
Examples & Analogies
Think of a bathtub that fills up with water from two faucets. Depending on how fast each faucet flows, the level of water in the bathtub will rise at a specific rate. Similarly, the problem examines how water from two rivers influences the storage in another body of water downstream.
Data of the Rivers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Ganga: Width, 700m; depth, 1.5m and average velocity, 0.9m/s
Brahmaputra: Width, 900m; depth, 1.2m and average velocity, 1m/s
Padma: Width, 1000m; depth, 1.6m and average velocity, 1.2m/s
Detailed Explanation
Here, we are given specific measurements of the Ganga and Brahmaputra rivers before they meet at the Padma River. These measurements include the width, depth, and average flow velocity, which are crucial for calculating the flow rates and understanding how the confluence affects the overall water storage in the Padma.
Examples & Analogies
Imagine measuring the size and flow of two rivers before they merge into a larger river. Just like knowing the dimensions of a garden hose helps understand how much water it can deliver, these measurements help us quantify the water entering the Padma River.
Control Volume Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we have a control volume like this. So, this is a no flow, this is a no flow. The flow will be only this, here and here and here. So, this is inflow, this is inflow, this is outflow.
Detailed Explanation
The concept of control volume is introduced to analyze the flow of water at the confluence. It helps in understanding how water enters and exits the system. By recognizing inflow from the two rivers and the outflow towards the Padma, we can apply the principles of mass conservation to determine if water is being lost or gained in storage.
Examples & Analogies
Think of a reservoir managed by a dam where water flows in through two tributaries and flows out through one main outlet. Managing the inflows and outflows is essential to ensure the reservoir does not overflow or run dry, similar to how understanding water dynamics at the confluence helps in flood prevention and water management.
Applying Conservation of Mass
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Apply the Reynolds transport theorem. You have the inflow and the outflow. There is no outflow in this case. In both the case you have inflow, which is negative here.
Detailed Explanation
This part emphasizes the application of the Reynolds transport theorem, a fundamental principle in fluid mechanics that helps in calculating changes in mass within a control volume. It provides a framework for understanding how inflows and outflows affect the storage of water at the confluence of the Ganga and Brahmaputra.
Examples & Analogies
Consider how a kitchen sink drains. If you turn on both taps and cover the drain, the sink will fill up (store water) until it either overflows or you drain it. This analogy represents the inflow from the rivers increasing water storage in the Padma while considering the potential for overflow.
Calculating Flows and Storage Changes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, substituting this value with have a negative or a positive of change in the storage.
Detailed Explanation
This section discusses the calculations needed to determine whether water is lost or gained after the confluence based on the supplied data for the Ganga and Brahmaputra rivers. It illustrates how to compute the flow rates and how these rates relate to changes in water storage in the Padma.
Examples & Analogies
It’s like measuring how much water comes from two hoses into a bucket (Padma) and figuring out if the bucket fills up, stays the same, or empties depending on how the hoses operate. By doing this, we can assess water availability in the Padma River downstream.
Results of the Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Finally, you will get the rate of change of height, that means in this the height will change 0.015 meter per second.
Detailed Explanation
Upon completion of the calculations, it indicates the rate of change of water height in the Padma River as a result of the inflows from the Ganga and Brahmaputra. This quantifiable result shows how much the flow dynamics have affected water levels, crucial for managing water resources effectively.
Examples & Analogies
Thinking about it in terms of daily life, this would be akin to knowing how fast a bucket fills every second. If you can predict the rate, you can better manage when to stop the water or how much to use for watering plants later.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Control Volume: A defined space used to analyze mass inflow and outflow.
-
Mass Flow Rate: Calculated using the equation Q = Width x Depth x Velocity.
-
Reynolds Transport Theorem: Connects integral equations describing fluid flow across a control volume.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of calculating inflow from the Ganga using given dimensions and flow rates.
-
Example of determining the change in storage after the confluence of Ganga and Brahmaputra into the Padma River.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Inflow, outflow, keep the mass, equal they shall be, none shall pass.
📖 Fascinating Stories
-
Imagine two rivers embracing each other, filling a large lake in their confluence, representing how their flows balance each other.
🧠 Other Memory Gems
-
Remember WDV: Width, Depth, Velocity for calculating flow rate!
🎯 Super Acronyms
Q = WDV for quick recall of flow rate calculation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Conservation
Definition:
The principle that mass cannot be created or destroyed in a closed system.
-
Term: Control Volume
Definition:
A defined region in space used to analyze the inflow and outflow of mass and energy.
-
Term: Reynolds Transport Theorem
Definition:
A fundamental theorem in fluid mechanics linking the change of quantity within a control volume to the movement of that quantity across the control volume's boundary.
-
Term: Flow Rate (Q)
Definition:
The volume of fluid that passes through a given surface per unit time, often expressed as cubic meters per second (m³/s).
-
Term: Inflows and Outflows
Definition:
The movements of water into and out of a given control volume.
-
Term: Dimensions (Width, Depth)
Definition:
Physical characteristics of a river cross-section used to determine flow rates.