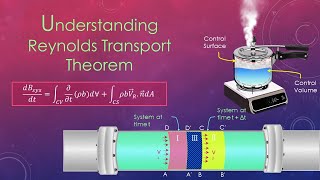
Applying Reynolds Transport Theorem
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Reynolds Transport Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we'll delve into the Reynolds Transport Theorem. Can anyone tell me what this theorem is about?

Isn't it something about how fluids behave in a control volume?

Exactly! It connects the movement of fluid through a control volume to the changes happening within that volume. It's crucial for analyzing fluid flows. Let’s explore it with the assumption that the flow is incompressible. What do we understand by incompressible flow?

That means the density of the fluid doesn’t change much, right?

Correct! If the Mach number is less than 0.3, density variations are negligible. So, what can we say about using density in our equations?

We can consider it constant to make the equations easier!

Right! That leads us to a simplified version of our mass conservation equations.

Remember, it’s all about balancing the inflow and outflow in that control volume while treating density as constant. Let’s move on to specific examples!
The Significance of Velocity Distribution
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let’s discuss velocity distribution in flow systems. Who can explain how velocity varies in a pipe?

I remember that it’s fastest in the center and zero at the walls due to friction.

Exactly! This variation is crucial, especially in turbulent flows. So how would we determine a constant average velocity then?

We could use integrals to compute it based on the velocity distribution over the area, right?

Correct! The average can be calculated by surface integrals, and we'll use this result in our mass flow calculations.

Always remember the relationship: average velocity equals the ratio of volumetric flow divided by the flow area. Let's summarize today's lesson.

We've learned that velocity field understanding is critical for analyzing mass conservation equations. Great job!
Practical Applications of RTT
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s put our knowledge into practice. Let’s consider a tank being filled with water. Can we set up a problem?

We could start by calculating the change in water height over time!

Exactly! With two inflows and no outflow, we can apply RTT. Can someone derive the expression for dh/dt?

Assuming we have the inflow rates, we can relate it to the change in height in that control volume.

Precisely! Managing all these inflows and considering our control volume properly is crucial. Calculate the change of storage effectively!

Well done everyone, we see how RTT helps us in real-life problems like tanks and rivers! Let’s summarize the insights from the example.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section emphasizes the significance of the Reynolds Transport Theorem in fluid mechanics, focusing on the implications of incompressible flow. It explores how density variations can be neglected under low Mach number conditions and provides insights into the conservation of mass equations, velocity fields, and the methods used for solving related problems.
Detailed
Detailed Summary
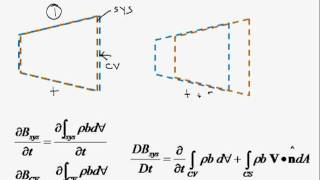
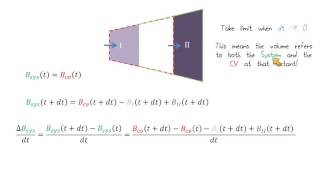
The Reynolds Transport Theorem (RTT) is a pivotal principle in fluid mechanics that connects the flow of a fluid into and out of a control volume to the rate of change of fluid properties within that control volume. This section highlights key aspects of RTT relevant to incompressible flows, emphasizing the following points:
- Incompressible Flow Assumption: When the flow Mach number is less than 0.3, density variations are negligible, allowing us to treat the fluid as incompressible. This simplification leads to more manageable equations and analysis.
- Mass Conservation Equation: The mass conservation equation remains applicable even when density is treated as constant. The equation simplifies the analysis to volumetric flow terms instead of mass flux, where mass flux is categorized as robust while using volumetric equivalents to ease calculations.
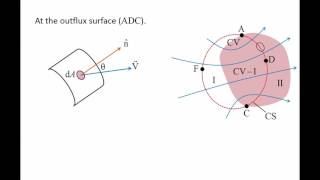
- Velocity Distribution: Understanding that velocity distribution varies across different flow scenarios is crucial. Velocity near boundaries (like pipe walls) is lower than at the center, leading to complex distribution in actual flow conditions. The concept of average velocity is used to model flow in systems where complex velocity fields exist.
- Control Volume Approach: Employing control volumes helps analyze the inflows and outflows accurately while ignoring how trapped gases (like air) might complicate calculations. The equations derived can describe various fluid systems, including simple tanks and complex flow interactions, like river confluence.
- Practical Applications: Examples provided reinforce these principles, illustrating calculations about inflow rates, outflow discharge, and conservation metrics, often relying on resolving average values across control surfaces.
Thus, mastering the Reynolds Transport Theorem and its implications for incompressible flow significantly simplifies the analysis of fluid mechanics problems.
Youtube Videos


![Get to know Reynolds Transport Theorem - part I [Fluid Mechanics]](https://img.youtube.com/vi/BwOnHIsgK_Q/mqdefault.jpg)



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Incompressible Flow
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, let me come in to the, if the flow is incompressible. Again, we have a lot of simplifications. Again, I can repeat it. The flow systems when you have mac number less than 0.3, okay, whether it is gas, whether it is a liquid or any flow system, if you think that the within the flow system the flow becomes less than the mac number less than 0.3, then there will be density variation, but that variation of density is much much negligible comparing to other components.
Detailed Explanation
In fluid dynamics, the Reynolds transport theorem helps us analyze fluid motion in a simplified manner. When the Mach number is less than 0.3, both gases and liquids can typically be treated as incompressible fluids because the density of the fluid does not vary significantly with pressure changes. This assumption simplifies calculations since we can treat density as a constant.
Examples & Analogies
Think of a water balloon. If you squeeze it gently (just like low Mach number flow), it barely changes volume. But if you were to squeeze a balloon filled with air hard, the air gets compressed. At low speeds, like the water balloon, the fluid behaves in a stable, incompressible manner.
Simplified Equations for Incompressible Flow
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When you have any flow systems, mac number is less than 0.3, so we can use flow as incomprehensible flow, density does not vary significantly. So, density becomes constant, as density becomes constant, as you know it, it is very simplified problem what we are going to solve.
Detailed Explanation
When we assume incompressibility in flow with a Mach number below 0.3, we can treat density as a constant value throughout the system. This significantly simplifies our calculations and leads to straightforward equations to work with in fluid dynamics. Essentially, rather than tracking varying densities, we focus on volume flow rates.
Examples & Analogies
Consider water flowing through a garden hose. Whether the water is pouring fast or slow, its density doesn’t change. In the same way, for low-speed flows (Mac < 0.3), we treat fluids like water in the hose as having a constant density.
Mass and Volumetric Flux
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, we can assume the flow is incompressible nature. Again, I am going to summarise that. When you have any flow systems, mac number is less than 0.3, so we can use flow as incomprehensible flow, density does not vary significantly. So, we can talk about volumetric flux.
Detailed Explanation
In incompressible flow scenarios, the concept of mass flux (mass flow per unit area) can be simplified to volumetric flux (volume flow per unit area). This means instead of worrying about how density affects mass flow, we can simply calculate how much volume flows through a specific area within a given time period.
Examples & Analogies
Think about how we measure water flowing from a tap. We often say liters per minute without needing to calculate density because water’s density remains constant. This simplifies how we determine how much water is available by just looking at the volumetric flow.
Velocity Profile in Pipe Flow
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If I have a pipe flow like this, you can anticipate it. As we discussed earlier, the velocity will be 0 near the wall, velocity will be maximum at the center and so there will be velocity distribution.
Detailed Explanation
In pipe flow, the velocity of fluid is not constant across the entire cross-section. It tends to be highest in the center and decreases to zero at the pipe walls due to friction. This creates a velocity profile, where knowing how this velocity changes across the surface is crucial for solving fluid dynamic problems.
Examples & Analogies
Imagine driving a car in a tunnel. The car in the center can speed along, while the slower vehicles near the walls can only crawl due to friction with the tunnel. This analogy helps visualize how fluid flow behaves in a pipe.
Importance of Velocity Field Knowledge
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, the velocity field knowledge is required for mass conservation equations.
Detailed Explanation
To apply conservation of mass laws in fluid dynamics, understanding how velocity varies in a flow field is critical. This information allows us to analyze how much fluid is entering, exiting, or changing within a control volume, ensuring our calculations are accurate and relevant to the flow situation.
Examples & Analogies
Think of a river delta, where water splits and flows in various channels. Knowing how fast the water moves helps us understand where it will deposit sediment and how the delta will change over time, similar to how we analyze flow in pipes.
Key Concepts
-
Reynolds Transport Theorem: Connects fluid flow across a control volume to internal changes.
-
Incompressible Flow: Assumes constant density for low Mach number conditions.
-
Mass Conservation: Key principle ensuring mass balance within a control volume.
-
Velocity Distribution: Describes how fluid velocities vary within a flow cross-section.
-
Control Volume: A defined space for analyzing fluid properties and dynamics.
Examples & Applications
Example of inflow and outflow rates in a tank using RTT.
Calculating the average velocity in a pipe with uncertain velocity profile.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a flow that won't compress, density stays the best; with RTT in view, fluid behavior we construe.
Stories
Imagine a tank filling with two rivers flowing in, the water height rising as balance begins—RTT helps track the win!
Memory Tools
To remember characteristics of incompressible flow: M for Mach number, D for Density constant.
Acronyms
RTT means Really Tight Tracking of Transport - keep fluid paths balanced!
Flash Cards
Glossary
- Reynolds Transport Theorem (RTT)
A theorem that relates the flow of a fluid into and out of a control volume to the rate of change of fluid properties within that control volume.
- Incompressible Flow
A flow condition where density remains constant with changes in pressure and temperature, generally applicable when the Mach number is below 0.3.
- Mass Conservation Equation
An equation that expresses the principle of mass conservation, indicating that the mass entering a control volume must equal the mass leaving, plus the change in mass within the volume.
- Volumetric Flow Rate
The volume of fluid passing through a section per unit time, typically measured in cubic meters per second (m³/s).
- Control Volume
A specified region in space through which fluid can flow, used for analyzing mass and energy within fluid mechanics.
- Velocity Distribution
The variation of fluid velocity across a flow cross-section, crucial when analyzing laminar and turbulent flows.
Reference links
Supplementary resources to enhance your learning experience.
