Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Incompressible Flow
Unlock Audio Lesson
Today, we are diving into the concept of incompressible flow. Does anyone know what defines a flow as incompressible?
Isn’t it when the density remains constant?
Exactly! Incompressible flow occurs when the Mach number is less than 0.3, meaning that density variations are negligible. Remember this acronym: 'MCD' - Mach number, Constant density, Negligible variation.
So, does this apply to both gases and liquids?
Yes! Whether it's air or water, as long as the Mach number stays below 0.3, we can treat it as incompressible.
To summarize, incompressible flow simplifies our equations by allowing us to treat density as a constant, making our computations much easier.
Mass Conservation and Control Volume
Unlock Audio Lesson
Now that we understand incompressibility, let’s connect this to mass conservation equations. Can anyone explain how mass conservation applies to a control volume?
It means that mass entering a control volume must equal mass leaving, plus any accumulation inside?
Great! We can express this mathematically using the equation for mass flux. Let's highlight a key point here: 'In = Out + Accumulation.'
What happens if the velocity distribution isn't uniform?
Excellent question! That’s where we use surface integrals to account for that non-uniformity. But if we assume the flow is uniform, calculations become much simpler.
To sum up, understanding velocity distribution is crucial in applying mass conservation to control volumes.
Practical Application: Example Problems
Unlock Audio Lesson
Let’s look at a practical example: filling a tank with two inflows. What do we need to consider in this case?
We would need the areas and velocities of the inflows to calculate the change in water height.
Correct! We apply the mass conservation principles to determine the change in height over time, denoted as dh/dt. Recall that the formula is: 'dh/dt = Q/A'.
What if the inflows have different velocities?
When velocities differ, we must account for each independently using their respective areas in our equation, leading to a more comprehensive analysis.
In essence, mastering these examples reinforces our understanding of control volumes and mass conservation in fluid mechanics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the concept of control volume is introduced in the context of fluid flow where compressibility is negligible. The section elaborates on the significance of the Mach number in determining flow behavior and explains mass conservation equations, emphasizing the role of velocity fields in analyzing fluid systems.
Detailed
Control Volume Application
This section delves into the fundamental principles of applying control volume concepts in fluid mechanics, specifically under the assumption of incompressible flow where the Mach number is less than 0.3. The primary focus is on the simplified equations that arise from the assumption of constant density in flow systems. The key equation derived is the volumetric flux equation, emphasizing the difference between mass and volumetric flow rate.
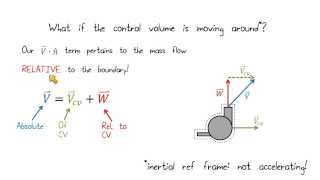
The importance of understanding the velocity vector's behavior in relation to control surfaces is highlighted, as the velocity distribution within a pipe or channel affects the mass conservation equations applied to control volumes. In scenarios involving uniform velocity, the equations can be simplified significantly, allowing for straightforward calculations of flow properties. Moreover, the section discusses various dilemmas in solving real-life fluid flow problems, stressing the need for determining velocity fields whether they are steady or unsteady, to correctly apply mass conservation laws.
Examples provided include practical applications involving tanks and environmental systems, illustrating the methodology for calculating changes in storage and seepage rate, depending on the governing flow parameters.
Overall, this section lays the groundwork for applying Reynolds transport equations and control volume methodologies to capture the essence of mass balance in fluid systems, guiding students in realistic problem-solving scenarios.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Incompressible Flow Assumptions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let me come in to the, if the flow is incompressible. Again, we have a lot of simplifications. Again, I can repeat it. The flow systems when you have mac number less than 0.3, okay, whether it is gas, whether it is a liquid or any flow system, if you think that the within the flow system the flow becomes less than the mac number less than 0.3, then there will be density variation, but that variation of density is much much negligible comparing to other components. So, we can assume the flow is incompressible nature. Again, I am going to summarise that. When you have any flow systems, mac number is less than 0.3, so we can use flow as incomprehensible flow, density does not vary significantly. So, density becomes constant, as density becomes constant, as you know it, it is very simplified problem what we are going to solve.
Detailed Explanation
In fluid dynamics, we often deal with different types of flows. When the Mach number (a measure of the speed of flow relative to the speed of sound) is less than 0.3, we can typically treat the fluid as incompressible. This means that the fluid density remains essentially constant throughout the flow, which significantly simplifies our calculations. In other words, even if there are small density changes, they are so minor that they can be ignored without impacting the overall problem significantly.
Examples & Analogies
Think of a garden hose: when water flows through it at low velocities, the water's density remains constant and does not compress much. However, if you speed up the water too much (like a rocket taking off), then you might have to consider compressibility effects, just like how air behaves under different speeds.
Volumetric vs Mass Flux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
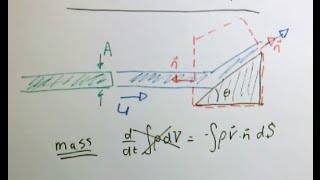
So, density varies negligible, as the density variation is not significant and beta equal to 1, so only this equation is left for us. Simple thing. This is very simple equation. DB sys = density * velocity * area + density * (density vector * normal vector) dA. Now, there, the scalar product of V and n and d A, okay, and density can come out. So, instead of the mass flux we are now talking about volumetric flux. That means, if you multiply the velocity into area, then what you get is unit volume per unit height, volumetric flux, okay? So, please do not confuse, this is a different equation.
Detailed Explanation
When dealing with incompressible flows, we transition from discussing mass flow to volumetric flow. In volumetric flow, we consider how much volume of fluid passes through a particular area in a given time. The equation incorporates velocity and the area through which the fluid passes, allowing us to estimate how much fluid is flowing without needing to include density, which remains constant.
Examples & Analogies
Imagine filling a pool with a garden hose. The amount of water flowing (volumetric flow rate) can be calculated simply by measuring the diameter of the hose and how fast the water flows out. You don’t need to worry about the density of water in this case because it’s consistent throughout the flow.
Understanding Flow Through Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If the inlet and outlet are one-dimensional, where, Q = A V. Only that we are not showing the density multiplication. If you multiply with a Q, the V into A is Q is discharge. So, Q = V alpha , is the discharge. So, most of the conservation of mass you write, it, since density is a constant, you make it come out from that equation. So, it looks like volumetric level we are comparing but all are mass conservation equations.
Detailed Explanation
In control volume analysis, we often look at one-dimensional flow where the mass flow rate (Q) can be simply expressed as the product of the cross-sectional area (A) and the average flow velocity (V). Here, we can simplify matters by treating density as a constant, allowing us to focus on volumetric relationships rather than mass relationships, thus simplifying our analysis.
Examples & Analogies
Think of pouring a specific amount of sand through a funnel. The area of the funnel and the speed at which you pour the sand dictate how quickly the sand flows out. If the density of sand were to change dramatically, it would complicate this flow, but if we treat it as constant (which is usually valid), we can focus on how fast it pours out relative to the area of the funnel.
Velocity Distribution in Pipes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, what I am looking at is again summarised here. To solve this mass conservation equation, I should have knowledge on the velocity field. I should know how the velocity varies or I should know whether the velocity is a constant or the velocity varies. If I know the velocity variations on this control surface, then I can solve the problem.
Detailed Explanation
Understanding how velocity varies within the flow is crucial for applying mass conservation principles. In pipe flow, for instance, the velocity is highest at the center and decreases towards the walls. This velocity distribution impacts calculations and assumptions we can make about the flow behavior.
Examples & Analogies
Picture a highway where cars move fastest in the center and slow down as they approach the edges. If you only pay attention to the average speed of all cars instead of their position, your understanding of traffic flow becomes less accurate—similarly, understanding velocity distribution in a pipe is essential for accurate flow analysis.
Uniform Velocity Distribution Assumption
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, basically, when you apply the mass conservation equation, your knowledge of velocity variation is important to you, how you are simplifying the velocity field on the control surface. That way we solve the problem. If you can understand properly, applying this Reynolds transport theorem and the simplification and put the numerical value, it does not take much time or much problem to solve any problem.
Detailed Explanation
Assuming uniform velocity distribution simplifies calculations but is not always realistic. It is crucial to assess if the flow can be approximated as uniform before applying mass conservation equations. This assessment helps ensure that our final conclusions and calculations are valid and realistic.
Examples & Analogies
Consider a bathtub where water is added evenly. If you assume all parts of the water are level (uniform), you can easily calculate how much time it takes to fill it. But if the water is splashing towards one side, then your assumption will lead to incorrect results. You must account for variations in flow to get accurate results.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Incompressible Flow: When the density of fluid remains constant, primarily applicable when the Mach number is less than 0.3.
-
Mass Conservation: A principle in fluid mechanics that states mass entering a system must equal mass leaving the system over time.
-
Velocity Distribution: Understanding the changes in fluid velocity across different cross-sections of a control volume is crucial for solving fluid problems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
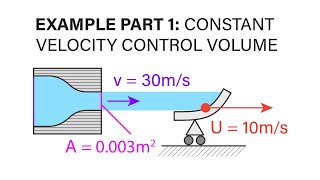
Example of flow in a tank being filled by two different inlets with different velocities.
-
Analysis of seepage in a channel and its impact on flow rates.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Incompressible flow, let it be known, Density stays constant, like a stone!
📖 Fascinating Stories
-
Imagine a large tank filled with water. Two pipes fill it up, but the water doesn't spill over because it's incompressible, like a perfectly packed crowd at a concert.
🧠 Other Memory Gems
-
Remember 'MCC' - Mach less than 0.3 means Constant density. Helps to understand incompressibility!
🎯 Super Acronyms
For mass conservation, use 'MIO' - Mass In equals Out. Simplifies our analysis.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Control Volume
Definition:
A specified region in space through which fluid flows, used to analyze mass and energy.
-
Term: Mach Number
Definition:
A dimensionless number that represents the ratio of the speed of flow to the speed of sound in that medium.
-
Term: Volumetric Flux
Definition:
The volume of fluid flowing per unit time through a given area.
-
Term: Mass Conservation
Definition:
The principle stating that mass cannot be created or destroyed in a closed system.