Volumetric Flux and Control Volume
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Incompressible Flow and Density
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're discussing incompressible flow. Does anyone know when we can treat a flow as incompressible?

Is it when the flow velocity is very low?

Good! Specifically, when the Mach number is less than 0.3, density variations are negligible, making calculations much simpler. We can assume density is constant.

So, we can use density in our equations without worrying about it changing?

Exactly! When density is constant, we simplify our mass conservation equations. Remember: 'Incompressible means density isn’t a variables!' This can be our mnemonic.

Can we apply this to both liquids and gases?

Yes, it applies to both, as long as the Mach number is low! Now let's summarize. We treat a fluid as incompressible when its Mach number is less than 0.3.
Volumetric vs. Mass Flux
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let’s talk about volumetric flux and how it relates to the concept of mass flux. Can anyone tell me what volumetric flux is?

Isn’t it the product of velocity and area?

Exactly! We denote it as Q = A * V. When we talk about volumetric flux, we simplify mass flux by pulling out the constant density. What’s the equation for mass flux then?

Is it density times volumetric flux?

Yes! It's crucial to see that even in volumetric form, we’re still dealing with mass conservation principles.

So, mass flux is still about conservation, right?

Correct! Remember: 'Mass Flux is in every flow' to keep it clear in your mind! Let's summarize: volumetric flux is related to flow area and velocity, while mass flux incorporates density.
Reynolds Transport Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’ll apply the Reynolds transport theorem. Does anyone know its significance in fluid dynamics?

It's used to relate the rates of change of a property within a volume to inflows and outflows?

Exactly! It helps us handle conservation equations for different properties. Why is knowing the velocity field necessary?

Because it affects how we calculate mass flows at different points!

Correct! Since velocity varies within a flow, recognizing that variation lets you determine mass or volumetric flows accurately. Remember: 'Velocity is the driver, control the flow!’

What happens if we consider a uniform velocity?

In that case, it simplifies our calculations a lot! To conclude: the Reynolds transport theorem connects inflow, outflow, and change within a control volume.
Practical Applications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s now discuss how these concepts apply in real situations. Can anyone think of a context where we use these principles?

Water flowing through pipes in plumbing!

Absolutely! We measure flow rates using volumetric flux there. Another example is how rivers interact with groundwater.

So, we could track water loss in rivers using these principles?

Yes! Remember: 'Every drop counts in the flow' to see the importance in every application! To wrap up today, we’ve covered how volumetric flux affects our handling of water systems in engineering.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the principles of volumetric flux within control volumes, emphasizing that when the Mach number is less than 0.3, fluid flow can be considered incompressible. This simplification allows for significant applications in mass conservation equations, particularly through the Reynolds transport theorem and understanding velocity fields.
Detailed
Detailed Summary
The section addresses the concepts of volumetric flux and control volume utilized in fluid mechanics. It begins by defining conditions for incompressible flow, highlighting that when the Mach number is below 0.3, the variation in density is negligible, allowing us to treat density as a constant. This provides simplifications that aid in solving various fluid dynamics problems.
Key equations such as the discharge equation (Q = A * V) emerge, allowing the calculation of mass conservation within a control volume. The discussion moves to how volumetric flux connects with mass flux and how these concepts can be applied in control volumes with one-dimensional inflows and outflows. By exploring the velocity distribution in different scenarios, the section illustrates how to apply the conservation principles effectively while emphasizing the importance of understanding the velocity field within a flow system.
Through examples, the section reinforces the idea that velocity fields significantly affect mass conservation equations, thereby illustrating how fluid mechanics principles apply to real-world situations.
Youtube Videos

![System Approach and Control Volume Approach [Fluid Mechanics]](https://img.youtube.com/vi/quK9rvsZTPA/mqdefault.jpg)






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Incompressible Flow Assumptions
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In flow systems where the Mach number is less than 0.3, we can assume the flow is incompressible. This means that density variations are negligible compared to other components of the flow, allowing us to treat density as a constant.
Detailed Explanation
When the Mach number, which is a ratio of the flow velocity to the speed of sound in the fluid, is below 0.3, we categorize the flow as incompressible. This classification simplifies our calculations since we do not need to account for variations in density as the flow system operates. By treating density as a constant, we simplify the equations involved in analyzing the flow.
Examples & Analogies
Imagine a bicycle tire. When you inflate it, the air inside compresses slightly, but if you keep the pressure low (similar to low Mach numbers in our flow systems), the air density changes very little and can be treated as a constant for practical purposes – making it simpler to calculate tire pressure and performance.
Mass Flux to Volumetric Flux
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The relationship between mass flux and volumetric flux can be established. Mass flux is related to the product of density and volumetric flow rate. When we simplify our analysis by treating density as constant, we can express mass flow as a function of volumetric flow.
Detailed Explanation
Mass flux refers to the mass of fluid passing through a given area per unit time, while volumetric flux pertains to the volume of fluid passing through an area over time. If density is treated as constant, we can derive volumetric flux by simply multiplying the velocity by the area, which significantly simplifies our calculations. This transition from mass flux to volumetric flux allows for easier analysis of fluid systems.
Examples & Analogies
Consider a garden hose. If you know the diameter of the nozzle and the speed of water coming out (velocity), you can easily calculate how much water flows out in a given time (volumetric flux). If you also take into account the density of water (which remains constant under normal circumstances), you can find out how much mass of water flows through the hose.
Velocity Distribution in Pipe Flow
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In pipe flows, the velocity distribution is not uniform. The velocity is zero at the pipe walls and maximum at the center. This velocity gradient impacts the flow characteristics.
Detailed Explanation
In any given pipe flow, we observe that velocity varies from the walls to the center due to friction. This creates a velocity profile where the fluid flows faster in the centers and slower at the walls. Understanding this distribution is essential for analyzing flow rates and pressure changes in pipes. Engineers often rely on the average velocity in such situations to simplify calculations without losing significant accuracy.
Examples & Analogies
Think of a river flowing through a canyon. The water in the center flows more quickly than the water near the sides where there is more friction with the canyon walls. This concept can be translated back to pipe flow, where we can visualize how fluid moves in a non-uniform way based on its contact with surfaces.
Importance of Velocity Knowledge in Fluid Mechanics
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Knowing the velocity field is crucial when applying conservation of mass equations. Whether the flow is uniform or varies significantly affects how we approach fluid problems.
Detailed Explanation
When dealing with fluid mechanics problems, it’s vital to understand how velocity changes throughout a control volume. Is the flow uniform across the area, or does it differ based on the conditions within the system? This knowledge guides which equations to use and how to manipulate them for accurate results. Inaccurate assumptions regarding velocity fields can lead to incorrect solutions and significant errors.
Examples & Analogies
Imagine measuring the wind speed in a room. If you only check the speed in one corner without considering the airflow across the whole space, you may miss areas where air is stagnant or moving much faster. In fluid dynamics, we need to capture the entire velocity field to correctly assess mass and energy balances.
Key Concepts
-
Volumetric Flux: The volume of fluid flowing per unit time and per unit area.
-
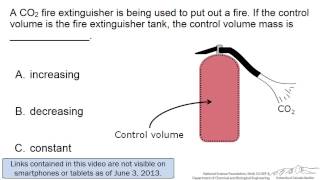
Control Volume: A defined space in fluid dynamics for analyzing mass and energy transfers.
-
Incompressible Flow: A flow regime in which density is treated as constant.
-
Reynolds Transport Theorem: A framework for relating changes in mass within a control volume to inflow and outflow.
Examples & Applications
Calculating the volumetric flow rate of water through a cylindrical pipe using Q = A * V.
Analyzing the conservation of mass in a river system where the inflow and outflow need to be balanced.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When Mach is under point three, density's fixed, it's easy to see!
Stories
Imagine a water tank where the flow stays steady. The speed of the water doesn't change much, so we don't worry about the heaviness of it — just focus on how fast it's leaving!
Memory Tools
Use the acronym 'FLOW' to remember: Flow velocities matter, Liters per time for volumetric analysis, Outflow equals inflow for conservation, Watch the Mach number!
Acronyms
Remember 'MASS' for mass conservation
**M**ass is conserved
**A**ny change applies
**S**urface integrates help
**S**imply the flow!
Flash Cards
Glossary
- Volumetric Flux
The volume of fluid flowing per unit time per unit area, typically expressed as Q = A * V.
- Control Volume
A defined region in space through which fluid may flow, used to analyze mass conservation.
- Incompressible Flow
A flow in which the fluid density remains constant, typically when the Mach number is less than 0.3.
- Mach Number
A dimensionless quantity representing the ratio of flow velocity to the speed of sound in the medium.
- Reynolds Transport Theorem
A theorem that relates the rate of change of a quantity within a control volume to its flow in and out.
Reference links
Supplementary resources to enhance your learning experience.
