Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Boundary Layer Equations
Unlock Audio Lesson
Good morning, everyone! Today, we're delving into boundary layer equations which arise from the Navier-Stokes equations under certain simplifications. Can anyone recall why we focus on boundary layers in fluid mechanics?
Is it because they help us understand the flow behavior near surfaces?
Exactly! Boundary layers are crucial because they influence drag and lift on objects. Now, does anyone know what the main equations we derive for boundary layers are?
I think we derive the mass conservation and momentum equations.
Right! We combine these to obtain the boundary layer equations. Remember, they can be solved numerically, which is significantly easier today than in Prandtl's time. Let's pause here and summarize: the equations we focus on are derived from the Navier-Stokes equations and tailored to fit the dynamics near surfaces.
Laminar Boundary Layers
Unlock Audio Lesson
Now, let’s talk specifically about laminar boundary layers. Can someone explain what laminar flow is?
Laminar flow is smooth and orderly, right? It operates at low Reynolds numbers?
Correct! In boundary layer contexts, we typically associate laminar flow with lower Reynolds numbers, under 1 log 10 to the power 5. Can anyone tell me how we calculate boundary layer thickness?
We use equations derived from the momentum and continuity equations!
Exactly! And from this, we find important parameters such as wall shear stress and skin friction coefficients, leading us to discuss displacement thickness. Remember: laminar flows have predictable behavior which simplifies solving these equations.
Displacement Thickness and Momentum Thickness
Unlock Audio Lesson
Let’s dive deeper into two important concepts: displacement thickness and momentum thickness. Can anyone define displacement thickness?
Is it the distance the streamline is deflected due to the boundary layer?
Yes! It represents how much the effective flow is displaced. And what about momentum thickness?
It must relate to the net momentum deficit due to the flow being slowed down in the boundary layer.
Correct! The momentum thickness gives insight into viscous drag acting on the plate. Calculate it by integrating the momentum flux deficit across the boundary layer—this helps us quantify skin friction in flows.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on the boundary layer approximations, emphasizing numerical solutions for laminar boundary layers and their characteristics, including displacement thickness and momentum thickness. The discussions draw upon historical contributions from key figures in fluid mechanics and provide insight into the complexities of turbulent boundary layers.
Detailed
Detailed Summary
In this section, we explore the Boundary Layer Approximation in detail, particularly focusing on laminar boundary layers. The key topics include:
- Numerical Solutions: We delve into deriving numerical solutions for laminar boundary layers, highlighting the techniques used today, which differ greatly from the methods available in the early 20th century when computed solutions were not feasible.
- Displacement and Momentum Thickness: We introduce the concepts of displacement thickness and momentum thickness, which are critical for understanding how velocity distributions behave across the layers in fluid dynamics. Displacement thickness refers to the effective change in flow due to the presence of a boundary layer, while momentum thickness quantifies the momentum deficit in a flow due to the boundary layer effects.
- Historical Context: Acknowledgment of contributions made by figures such as Prandtl and Blasius in developing these concepts is paramount, illustrating the progress from hand-calculated approximations to sophisticated computational techniques we have today.
- Application and Significance: Understanding boundary layers is essential in various fields, including aerospace and mechanical engineering, as they directly impact drag forces and lift in moving bodies through a fluid.
Overall, this section aims to provide a thorough understanding of laminar boundary layers and paves the way for introducing turbulent boundary layers.
Youtube Videos
![[Fluid Dynamics: Boundary layer theory] Turbulent Boundary Layer](https://img.youtube.com/vi/3NV5n2bUu0g/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Boundary Layer Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Good morning. Let us discuss about boundary layer approximations what we have been discussing on in the last two classes. In the last class we have derived boundary layer equations which is the approximations of Navier-Stokes near to a boundary layer formations to a flow past in a flat plate which is a very simplified conditions.
Detailed Explanation
In this introduction, the professor emphasizes the focus on boundary layer approximations, which are derived from the Navier-Stokes equations. These equations describe fluid motion in simplified conditions, particularly concerning flow over a flat plate. The boundary layer is a crucial area where the fluid's velocity changes from zero (at the wall due to the no-slip condition) to the free stream velocity. Understanding boundary layers is essential in fluid mechanics, as they greatly affect drag and lift forces experienced by bodies moving through a fluid.
Examples & Analogies
Think of a river flowing over a flat rock. The water at the surface moves freely, but the layer of water in direct contact with the rock (the boundary layer) is slowed down due to friction. The boundary layer impacts how much water (or how swiftly) can flow around obstacles, just like how fluid flows around the edges of a flat plate.
Laminar Boundary Layer Solutions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Today we will talk about the laminar boundary layers, laminar boundary layers solutions. Then we will talk about a concept of displacement thickness, momentum thickness and introductions at the flat plate boundary conditions for the turbulent flat plate boundary layers.
Detailed Explanation
This chunk focuses on laminar boundary layers, where fluid flow is orderly as opposed to turbulent. The professor introduces key concepts such as displacement thickness and momentum thickness, which are critical in analyzing boundary layer behavior. Displacement thickness represents how much the boundary layer 'displaces' the outer flow, while momentum thickness relates to the momentum deficit within the boundary layer. Both concepts are essential to understanding the effects of boundary layers on forces like drag and lift.
Examples & Analogies
Imagine a train moving along a track. The air in contact with the train's surface is 'pushed back,' creating a layer of slower-moving air just like the layers of fluid near a flat plate. Displacement thickness can be thought of as how much the outer airflow has to adjust due to the presence of the train, while momentum thickness considers how much 'push' or energy is lost in that slower layer of air.
Boundary Layer Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
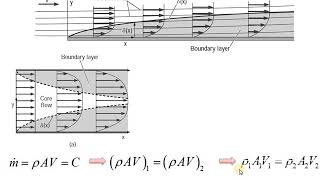
we are talking about laminar boundary layers equations. okay. So as you remember it the boundary layer equations what we derive it first is the mass conservation which is very simple as again I am repeating it for two-dimensional incompressible flow velocity divergence which is equal to del u by del x del v by del y.
Detailed Explanation
Here, the professor is reminding students of the fundamental boundary layer equations, particularly focusing on mass conservation in fluid flow. For laminar flow, the equations are simpler and follow the continuity principle that states mass cannot be created or destroyed within a flow. The divergence of the velocity field must equal zero, ensuring that the total mass flow is constant across sections of the flow. This principle is crucial for deriving the subsequent equations that govern boundary layer dynamics.
Examples & Analogies
Consider a pipe carrying water. The conservation of mass means that if water flows into the pipe at a certain speed and volume, the same amount of water must exit at the same speed. If the pipe narrows, the water speeds up to ensure the same volume flows through per second—this is akin to how mass conservation operates in boundary layers.
Solving Boundary Layer Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
if I look it as we derive it the linear momentum equations linear momentum equations and Bernoulli's equations both we combine it to get it the boundary layer equations in this form the basically x direction equations for steady incompressible flow.
Detailed Explanation
In this chunk, the professor explains the process of combining the linear momentum equations and Bernoulli's equations to formulate the boundary layer equations. This combination allows for a thorough analysis of fluid behavior under specific conditions—steady-state, incompressible flow—resulting in simplified equations that can be used to derive velocity profiles and shear stresses within the boundary layer. It highlights the importance of these equations in predicting fluid behavior near solid boundaries.
Examples & Analogies
When mixing a cake batter, you combine dry and wet ingredients, just as the professor combines different physics equations. If the ingredients are mixed well (properly solving the equations), you'll get a batter with the right consistency (accurate predictions about fluid flow). If not mixed well, you might end up with a lumpy batter, which would be like having inaccurate fluid dynamics predictions.
Computational Solutions to Boundary Layer Problems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if you look at the boundary layers, equations are not that difficult to solve today as compared to 120 years back.
Detailed Explanation
The professor highlights the advancements in computational techniques that have made solving boundary layer problems more accessible than in the past. With modern computing power and numerical methods, engineers can simulate complex fluid flows more accurately and efficiently than ever before. This accessibility helps engineers and scientists to predict boundary layer behavior and its effects on performance metrics, such as drag forces, quickly and reliably.
Examples & Analogies
Think of how navigation systems used to rely on paper maps—time-consuming and often difficult to update! Nowadays, GPS technology allows for real-time navigation with ease, adapting to changing conditions like road closures or traffic. Similarly, computational fluid dynamics uses complex algorithms to 'navigate' through fluid flow problems much more efficiently than the manual calculations of the past.
Understanding Displacement Thickness
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look at more details if I looking it from the edge of a plate as I go and if I sketch the boundary velocity distributions this is what the boundary layers.
Detailed Explanation
The concept of displacement thickness is introduced here, which is about how a boundary layer displaces surrounding fluid. By understanding how the velocity distributions change at the plate edge, students can visualize how the shape of velocity profiles inside and outside the boundary layer are affected. Displacement thickness is crucial for predicting the effective area over which fluid exerts force, and thus influences drag and lift calculations.
Examples & Analogies
Imagine a country road that suddenly narrows to a single lane; cars in the single lane must slow down, affecting traffic flow. Just like the road constrains the flow of cars, the boundary layer constrains the surrounding fluid flow, displacing it and changing its characteristics.
Momentum Thickness and Shear Stress
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we come to the momentum thickness which is not big the concept which is already we talk about shear stress displacement thickness also the wall shear stress.
Detailed Explanation
The momentum thickness concept connects back to shear stress and fluid momentum distribution across the boundary layer. Momentum thickness defines the momentum deficit caused by the boundary layer; it quantifies the difference in momentum between the flow inside the boundary layer and that of the outer flow. Understanding this helps engineers predict drag forces more accurately, as shear stress directly impacts the overall performance of surfaces in fluid flow.
Examples & Analogies
Think about a sponge absorbing water—though most of the sponge is soaked through, the edges may not absorb as much due to the 'skin' of the sponge. The momentum thickness acts similarly, indicating how much momentum is 'lost' or altered near the boundaries compared to the main flow, which is crucial in calculating forces on surfaces like wings or hulls.
Turbulent Boundary Layers Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When you go for the turbulent boundary layers just conceptually I will discuss with you.
Detailed Explanation
This chunk introduces the complexity of turbulent boundary layers, which are significantly different from laminar flows. In turbulence, flow patterns become chaotic and unpredictable, making direct calculations challenging. Instead of deriving equations, empirical data often guide the understanding of turbulent flows, helping to develop reliable models and approximations for things like velocity distributions and shear stresses. This topic underscores the advanced nature of turbulence studies in fluid dynamics.
Examples & Analogies
Think of a crowded market; movement is chaotic, and it’s hard to predict how people will navigate. That's like turbulent flow—unpredictable and influenced by many factors. In contrast, in a quiet store (laminar flow), everyone moves in a straight, organized path. Studying these chaotic interactions requires sophisticated methods and approximations, just like organizing that market scene would need careful planning.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Numerical Solutions: Techniques for solving laminar boundary layer equations using modern computation.
-
Displacement Thickness: A measure of how much the effective streamline is shifted due to boundary layer effects.
-
Momentum Thickness: Quantifies the momentum deficit caused by boundary layer formations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a wind tunnel experiment, the boundary layer thickness can be calculated to ensure laminar flow is maintained for accurate measurements of drag.
-
The principles of displacement thickness can be applied to calculate the effective force acting on an airplane wing due to changes in airspeed.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In laminar flow where layers glide, the displacement has to coincide.
📖 Fascinating Stories
-
Imagine a flat plate in a smooth stream—a slight curve is formed, that's the displacement theme.
🧠 Other Memory Gems
-
Remember D and M for Depth and Momentum, D is for Displacement and M for how we keep the forces in control.
🎯 Super Acronyms
DMT
- Displacement and Momentum Thickness helps in tracking flow patterns.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Boundary Layer
Definition:
The region of fluid near a boundary where the effects of viscosity are significant, causing velocity gradients.
-
Term: Laminar Flow
Definition:
A smooth, orderly flow regime characterized by parallel streamlines and low Reynolds numbers.
-
Term: Displacement Thickness
Definition:
The distance by which a streamline is deflected from its undisturbed position due to a boundary layer.
-
Term: Momentum Thickness
Definition:
A measure of the momentum deficit in the flow attributed to the boundary layer presence.
-
Term: Shear Stress
Definition:
The stress component parallel to a material's surface, influenced by fluid dynamics in boundary layers.