Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Boundary Layer Theory
Unlock Audio Lesson
Good morning class! Today, we're diving into the fascinating topic of boundary layers. Can anyone explain what a boundary layer is?
Is it related to the layer of fluid that is directly influenced by a solid boundary, like a wall?
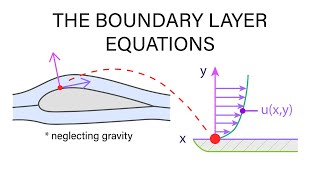
Exactly, Student_1! The boundary layer is the thin region of fluid near a solid surface where viscosity is significant. This affects how the fluid flows and exerts forces like drag. Now, can anyone tell me why understanding boundary layers is important?
It helps in predicting drag forces on objects, right?
That's correct! Understanding drag is crucial for aircraft design, automobile aerodynamics, and many engineering applications. Great job! Now, what do we use to describe the flow within these boundary layers?
We use boundary layer equations!
Correct! We'll focus on two main equations: the mass conservation equation and the momentum equation. Let’s summarize what we’ll be discussing today.
Mass Conservation in Boundary Layers
Unlock Audio Lesson
Let’s look at the mass conservation in boundary layers. The equation can be stated as \( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 \). Who can break down what this means?
It means that the change in velocity in the x-direction affects the change in the y-direction, keeping the mass flow constant.
Exactly, Student_4! This is critical for analyzing flow past a flat plate. Now, what do we call the velocity 'u' here?
U is the free stream velocity, right? It’s the velocity far from the boundary.
Yes! The velocity component 'v' describes how the fluid moves vertically in the boundary layer. Let's look at how this leads into the momentum equation.
Momentum Equation in Boundary Layers
Unlock Audio Lesson
When we derive the momentum equations for boundary layers, we simplify them significantly. The form we derive is \( \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = \nu \frac{\partial^2 u}{\partial y^2} \). Can anyone tell me about the parameters replaced in this equation?
U turned into v, and ν represents kinematic viscosity, right?
Exactly! This equation is easier to solve than the full Navier-Stokes equations. What happens to these equations as we utilize numerical methods?
We can solve them much faster, especially with high-performance computers!
Great point! Solving these equations numerically allows us to explore complex flow scenarios with much more ease. Let’s dive deeper into concepts like displacement thickness next.
Displacement Thickness
Unlock Audio Lesson
Displacement thickness is a term that helps us assess how the mass flow is changed due to the boundary layer. Can someone give me an example of where this applies?
It sounds like it would affect the drag force that acts on the surface!
Exactly! It gives us an idea of where to place the effective boundary, like an 'apparent wall' concept. So how do we calculate this displacement thickness?
I remember it involves a definite integral with the velocity profile.
Correct! The formula allows us to define the integral from zero to infinity for determining the speed deficit in the boundary layer. Excellent work!
Momentum Thickness
Unlock Audio Lesson
Next, we discuss momentum thickness. This also relates to drag, correct?
Yes, it represents the momentum deficit due to the boundary layer effects, right?
Spot on! The momentum thickness helps us estimate shear stress on the plate. Can you recall the formula for momentum thickness?
It’s the integral of velocity distribution over the free stream velocity, right?
Yes! This is a key concept; understanding it helps us connect how both displacement and momentum thickness play into the calculations for drag. Let's summarize our session.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on the boundary layer approximations for laminar flows, detailing the mass conservation and momentum equations. It also introduces key concepts such as displacement thickness, momentum thickness, and local skin friction factors, ultimately emphasizing the importance of these factors in understanding drag forces due to boundary layer effects.
Detailed
Boundary Layer Equations
This section delves into the boundary layer equations derived from the Navier-Stokes equations for fluid flow past a flat plate. It highlights the approximations necessary for understanding laminar boundary layers, including:
- Mass Conservation: The mass conservation equation for two-dimensional, incompressible flow, expressed as
\[ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 \]
where \( u \) and \( v \) are velocity components in the x and y directions, respectively.
- Momentum Equation: A simplification of the momentum equations to the boundary layer context, yielding a parabolic form that is simpler to solve than the full Navier-Stokes equations.
- Displacement Thickness: A term introduced to measure the effective change in mass flow due to the presence of the boundary layer, defined mathematically by the deficit of mass flow in the boundary layer compared to the free stream.
- Momentum Thickness: Related to the drag on the plate, quantifying the loss of momentum due to the boundary layer.
In this context, it is emphasized that solving these equations today is computationally feasible, unlike over a century ago. Historical contributions from Prandtl and his students to the understanding of boundary layers are acknowledged, including the conceptual evolution of boundary layer thickness estimation and the implications on drag and lift forces acting on solid surfaces in a fluid flow.
Youtube Videos
![[Fluid Dynamics: Boundary layer theory] Turbulent Boundary Layer](https://img.youtube.com/vi/3NV5n2bUu0g/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Boundary Layer Approximations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Good morning. Let us discuss about boundary layer approximations what we have been discussing on in the last two classes. In the last class we have derived boundary layer equations which is the approximations of Navier-Stokes near to a boundary layer formations to a flow past in a flat plate which is a very simplified conditions.
Detailed Explanation
In this introduction, the speaker emphasizes that the discussion will continue from previous classes about boundary layer approximations. Boundary layers are thin regions near a surface where the flow of fluid is affected by the surface itself, and the approximations simplify the complex Navier-Stokes equations, which describe fluid motion. Specifically, the context is a flat plate, which eases computation of the flow behavior.
Examples & Analogies
Think of boundary layer approximations like the air swirling around the surface of a car as it speeds down the highway. The air closest to the car's body moves slower compared to air further away, similar to how the fluid flow behaves near a flat plate.
Mass Conservation and Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if I look it as we derive it the linear momentum equations linear momentum equations and Bernoulli's equations both we combine it. to get it the boundary layer equations in this form the basically x direction equations for steady incompressible flow.
Detailed Explanation
This chunk discusses the equations that are crucial for understanding the fluid dynamics within the boundary layer. The mass conservation equation ensures that the mass flow rate remains consistent, while the momentum equations account for forces acting on the fluid particles. The combination leads to simplifications that help in deriving the boundary layer equations relevant for practical applications like designing aircraft wings or measuring fluid flows.
Examples & Analogies
Imagine you are pouring water through a funnel. The steady inflow at the top needs to equal the outflow at the bottom. This is similar to mass conservation in fluid mechanics, where the conservation of mass must hold true, especially near surfaces where boundary layers form.
Boundary Layer Thickness and Shear Stress
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So this is the equations which is a parabolic form okay, parabolic equations. as compared to the Navier stoke equations solving these two equations are easy because you know it from these two equations we can get a solutions of u and v and from that solutions we can get it what will be the layer thickness, what will be the wall shear stress.
Detailed Explanation
This part explains that the equations governing boundary layers can be reduced to a simpler parabolic form, which makes them easier to solve compared to the more complex Navier-Stokes equations. Knowing the flow velocity components within the boundary layer allows engineers to compute important factors like the thickness of the boundary layer and the shear stress at the wall, which are essential for predicting how a fluid will behave around objects.
Examples & Analogies
Picture a river flowing over a flat surface. At first glance, it looks smooth, but as water flows past rocks, it slows down near the surface of the rock—this is similar to how flow behaves in a boundary layer. The thickness of that slower-moving water represents the boundary layer, and engineers use this thickness to understand forces like drag.
Displacement Thickness Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The basically as we know it the boundary layer thickness developments happens it okay. The regions which is closer to that boundary layer formations are happening it.
Detailed Explanation
Displacement thickness accounts for the reduction in flow velocity caused by the boundary layer. It is the distance by which the location of the outer streamlines are displaced due to the slower speeds of fluid particles near the surface. This concept helps in visualizing how the effective area through which the fluid flows is altered by the boundary layer.
Examples & Analogies
Consider the flow of traffic on a highway. As cars approach a toll booth, they slow down, causing the flow of traffic behind them to adjust. The space occupied by the cars experiencing the slowdown is like the displacement thickness that affects how much effective road space is available ahead.
Momentum Thickness Explained
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we come to the momentum thickness which is not big the concept which is already we talk about shear stress displacement thickness also the wall shear stress.
Detailed Explanation
Momentum thickness provides another metric related to the flow of fluid within the boundary layer. It measures how much momentum is lost due to the presence of the boundary layer relative to an imaginary one without it. Both momentum and displacement thickness help in understanding flow characteristics and forces acting on surfaces.
Examples & Analogies
Think of momentum thickness like the pressure difference caused by a group of people trying to exit through a narrow door. The force and speed with which they exit are reduced compared to if the door was wide open, illustrating how momentum is ‘thinned out’ by the limitations of the boundary conditions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Boundary Layer: A thin region in a fluid flow affected by viscosity near a solid surface.
-
Mass Conservation Equation: A fundamental principle stating that mass cannot be created or destroyed.
-
Momentum Equation: Describes how momentum is conserved in flow context.
-
Displacement Thickness: Effective thickness that accounts for mass flow reduction due to boundary layer.
-
Momentum Thickness: A measure of how much momentum is lost due to the influence of the boundary layer.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of displacement thickness calculation in a wind tunnel setup.
-
Analyzing momentum thickness in drag forces on flat plates.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In layers fine, near surfaces they sway, / Viscosity holds the flows in a ballet.
📖 Fascinating Stories
-
Imagine a river flowing smoothly until it meets a rocky bank. The water slows down and swirls, creating a boundary layer that affects everything from speed to pressure.
🧠 Other Memory Gems
-
D-M-M: Displacement - Momentum - Mass, remember the key flow factors when discussing layers.
🎯 Super Acronyms
B-L-M
- Boundary Layer Momentum – focuses on drag dynamics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Boundary Layer
Definition:
A region near a solid boundary where the flow velocity is affected by viscosity.
-
Term: Mass Conservation Equation
Definition:
An equation expressing the principle that mass is conserved within a control volume.
-
Term: Momentum Equation
Definition:
Describes the conservation of momentum in a flow, simplified for boundary layer analysis.
-
Term: Displacement Thickness
Definition:
The thickness of an apparent layer that accounts for the reduction in mass flow due to viscosity effects in the boundary layer.
-
Term: Momentum Thickness
Definition:
A measure of momentum deficit in the boundary layer which affects drag on surfaces.