Conclusion on Boundary Layer Approximations
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Boundary Layer Approximations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Good morning, everyone! Today we will discuss the essential concepts of boundary layer approximations in fluid mechanics. Can anyone tell me what a boundary layer is?

Isn't it the region near a surface where the effects of viscosity are significant?

Exactly! The boundary layer is the thin region adjacent to a surface where shear stress primarily occurs due to viscosity. This concept is crucial when examining flows such as those involving flat plates.

What's the importance of analyzing these boundary layers?

Great question! Studying boundary layers allows us to understand drag forces and other forces acting on surfaces. Remember the acronym 'B.L.A.' - Boundary Layer Analysis helps in predicting drag!

Can we see practical applications of this?

Certainly! Applications include aircraft design, marine vessels, and even predicting weather patterns. Let's proceed to discuss laminar boundary layers in detail.
Laminar Boundary Layer Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

In laminar flow, we can derive boundary layer equations to describe velocity distributions. Who can share the mass conservation equation for boundary layers?

It's the equation indicating that the divergence of the velocity field is equal to zero in two-dimensional incompressible flows!

Absolutely right! This forms the basis for our boundary layer equations, particularly when combined with momentum equations. Let's break them down.

What do we mean by boundary layer thickness?

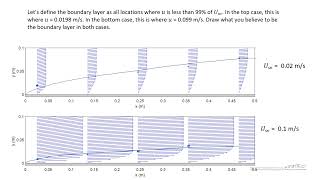
Boundary layer thickness defines how far from the surface the effects of viscosity are felt. The thickness influences drag and lift in real-world applications. To remember it, think 'T.B.L.' - Thickness Affects Behavior of Lift!
Displacement and Momentum Thickness
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Displacement thickness accounts for the 'deflection' of streamlines due to boundary layer flow. Who can explain how we define this mathematically?

It accounts for the mass flow deficit due to the presence of boundary layers compared to free stream flow.

Correct! Remember to visualize it as a deflection when thinking of displacement thickness. Now, what about momentum thickness?

Momentum thickness relates to the drag force exerted on the surface from the boundary layer.

Exactly! It’s defined as the net momentum flux across the boundary layer. To keep it memorable, think 'M.T.D.' - Momentum Thickness = Drag!
Contributions to Boundary Layer Theory
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's talk about who laid the foundation for boundary layer theory. Can anyone name a significant figure?

Is it Ludwig Prandtl? He developed many concepts regarding boundary layers.

Yes, Prandtl is a pivotal figure! He and his PhD students developed solutions while relying heavily on manual computation techniques—something difficult today!

What were his main contributions?

He introduced boundary layer concepts, derived equations, and explained how shear stress plays a role in fluid flow separation. Use 'P.P.' for Prandtl's Pioneering - he helped us understand turbulence!
Overview of Turbulent Boundary Layers
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

We’ve focused on laminar flows; what can we describe for turbulent boundary layers?

Turbulent flows involve chaotic properties and high mixing, making them complex to analyze.

That's right! Remember 'C.A.M.' - Chaotic and Mixed. Turbulent flows generally present higher wall shear stress than laminar flows due to their chaotic nature.

Are there empirical equations for turbulent flows?

"Yes, such as the one-seventh power law and log law, which help us estimate turbulent velocity profiles.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The conclusion on boundary layer approximations summarizes various aspects of the topic including laminar boundary layer concepts, displacement and momentum thickness, solutions derived from boundary layer equations, and the historical contributions of key figures in the field of fluid mechanics.
Detailed
Conclusion on Boundary Layer Approximations
In this section, we delve into the fundamental concepts surrounding boundary layer approximations in fluid mechanics. Boundary layers are critical in understanding flow characteristics, especially near surfaces such as flat plates. We primarily focus on laminar boundary flow and the development of key parameters including displacement thickness and momentum thickness.
Historically, significant contributions from Prandtl and his students provided early solutions to boundary layer equations, despite the absence of computational resources available today. The section highlights how to derive solutions for boundary layer equations through simplified numerical methods.
We also explore the coefficients defining wall shear stress and local friction factors, illustrating their dependence on boundary layer behavior. In turbulent flows, we contrast these findings, showcasing their empirical nature, and the constant effort in the study of turbulent dynamics through simplified empirical equations like the one-seventh power law and log law.
Overall, this section encapsulates an introduction to boundary layer theory primarily aimed at undergraduates and lays the groundwork for further exploration into more complex turbulent boundary conditions.
Youtube Videos



![[Fluid Dynamics: Boundary layer theory] Turbulent Boundary Layer](https://img.youtube.com/vi/3NV5n2bUu0g/mqdefault.jpg)





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Boundary Layer Approximations
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
With this let me conclude boundary layers approximations as I said it very beginning we are talking about introductory levels and these are the 3 equations as we talk about boundary layer equations displacement and momentum equations and that is what we have derived it.
Detailed Explanation
In this conclusion, the lecturer summarizes the key concepts discussed throughout the course regarding boundary layer approximations. The focus is on introductory concepts targeted for undergraduate students. The main equations regarding boundary layers, including the boundary layer equations, the displacement thickness, and the momentum thickness, have been covered in detail during the lectures.
Examples & Analogies
Think of learning about boundary layers as visiting different sections of a museum. At each section, you examine specific artifacts (equations) that tell a part of the overall story (fluid flow). The conclusion is like the museum guide’s summary—it ties everything together by reminding you of all the main points studied and how they relate to each other.
Applications of Boundary Layer Concepts
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
many of gate or engineering service things are comes under these displacement thickness, momentum thickness and some part of how to estimate the boundary layer thickness that is things are there.
Detailed Explanation
The lecturer emphasizes the practical applications of the concepts of boundary layers, particularly highlighting displacement thickness and momentum thickness. These concepts are crucial for various engineering applications, such as designing efficient aircraft wings and predicting drag forces that affect the performance of vehicles moving through fluids. Understanding these properties allows engineers to make informed decisions during the design process.
Examples & Analogies
Imagine designing a car. Engineers need to understand how air flows over the car’s body—this is where boundary layer concepts come into play. By knowing how thick the boundary layer is (displacement thickness) and how it impacts drag (momentum thickness), engineers can shape the car's exterior to minimize air resistance and improve fuel efficiency, just like sculptors refine their art to achieve the best form.
Review of Key Equations
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
that is what is the subject matter emphasis on the basic equations that the boundary layer approximation is dependent, we emphasize that displacement thickness and momentum thickness are derived from the analysis of boundary layer equations.
Detailed Explanation
The lecturer revisits the fundamental equations that underpin boundary layer approximations, reiterating the importance of understanding how these equations derive the concepts of displacement thickness and momentum thickness. These equations help simplify complex fluid flow problems and make them manageable, especially in practical engineering scenarios. By mastering these equations, students gain tools necessary for analysis and design in fluid mechanics.
Examples & Analogies
Consider learning to cook using a recipe. The main ingredients represent the key equations, while the steps of the recipe are like the processes that lead to your final dish (boundary layer concepts). Just as understanding the ingredients and steps helps you cook better meals, mastering the key equations enables engineers to analyze and optimize designs for fluid dynamics.
Key Concepts
-
Boundary Layer: The region where viscous effects are significant in fluid flow.
-
Displacement Thickness: Represents the deflection of streamlines due to the flow of a boundary layer.
-
Momentum Thickness: Indicates the drag force on surfaces related to boundary layers.
-
Laminar Flow: A smooth, orderly type of flow.
-
Turbulent Flow: A chaotic, irregular type of fluid motion.
-
Shear Stress: Stress acting parallel to a surface.
Examples & Applications
In aircraft design, understanding boundary layers helps to minimize drag, thus improving fuel efficiency.
In bridge engineering, analyzing boundary layers helps to ensure structural integrity against fluid forces.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Boundary layers are thin but mighty, they stick close, making flow tighty!
Stories
Once there was a fluid traveling swiftly, but it encountered a flat plate. As it approached, it slowed down, forming a boundary layer that contained its effects, making it dance gently along the surface.
Memory Tools
To remember thickness concepts: 'D for Displacement, M for Momentum - both measure how flow intends to function!'
Acronyms
B.L.A. - Boundary Layer Analysis helps understand flows around objects.
Flash Cards
Glossary
- Boundary Layer
The thin region adjacent to a surface where viscous effects are significant.
- Displacement Thickness
A measurement representing the deflection of streamlines due to the presence of the boundary layer.
- Momentum Thickness
A measure related to the drag force acting on a surface due to the presence of a boundary layer.
- Laminar Flow
A type of fluid flow characterized by smooth, orderly motions, typically at lower velocities.
- Turbulent Flow
A type of fluid flow characterized by chaotic and irregular fluid motion, typically at higher velocities.
- Shear Stress
The stress component parallel to a material cross-section, crucial in boundary layer analysis.
Reference links
Supplementary resources to enhance your learning experience.
