Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Reynolds Number
Unlock Audio Lesson
Today, we'll discuss the Reynolds number and why it's fundamental in understanding fluid flow. Who can tell me what factors might influence the flow of a fluid?
I think things like velocity and viscosity are important!
Exactly! The Reynolds number combines these factors: it’s defined as the ratio of inertial forces to viscous forces. Can anyone remember the formula for Reynolds number?
Isn't it Re equals density times velocity times length over viscosity?
Right! It can be simplified to the formula: $Re = \frac{\rho u L}{\mu}$. Let's break this down into components.
What do each of those symbols mean?
Great question! $\rho$ represents fluid density, $u$ is the mean flow velocity, $L$ is a characteristic length like the diameter of a pipe, and $\mu$ is the dynamic viscosity. Understanding these helps us understand flow behavior.
To remember, think of the acronym DUM-VD: Density, Velocity, and is like a Measure of Viscosity and Diameter. This helps encapsulate the crucial aspects contributing to Reynolds number.
What happens to flow characteristics when Re changes?
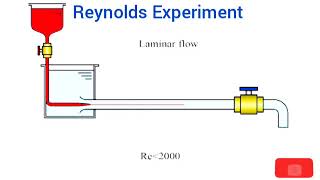
Good point! As Re increases, flows may transition from laminar to turbulent. Typically, flows with Re less than 2000 are laminar, while those greater than 4000 tend to be turbulent. This is crucial for engineers to know when designing systems.
So by understanding Reynolds number, we can predict and model fluid flow accurately. Remember, this is a critical concept in all of fluid mechanics!
Calculating Reynolds Number
Unlock Audio Lesson
Now let's learn to calculate Reynolds number with some practical examples. Who remembers the formula?
It’s Re equals density times velocity times length over viscosity!
Exactly! Let's say we have water flowing in a pipe with a diameter of 0.1 meters, a flow velocity of 1 m/s, and viscosity of 0.001 Pa·s. What is the density of water?
The density of water is about 1000 kg/m³!
Yes! Now, plug the values into the formula. Can anyone calculate Reynolds number?
I’ll try! Re = (1000 kg/m³ * 1 m/s * 0.1 m) / 0.001 Pa·s = 100,000.
Great work! That means the flow is turbulent since it’s above 4000. This understanding allows engineers to design systems that work effectively in different flow regimes. Remember: High Re means turbulent mix!
Applications of Reynolds Number
Unlock Audio Lesson
Let's discuss where we apply Reynolds number practically. Can anyone think of applications?
How about in pipeline design?
Exactly! Engineers use Reynolds number to determine the flow type in pipelines, ensuring efficient transport of fluids. What about in aviation?
In designing airplane wings to reduce drag?
Correct! The flow around the wing can be modeled as laminar or turbulent using Reynolds number to optimize design for performance and safety.
Can it be used in environmental engineering?
Absolutely! It helps in understanding river flows, pollutant dispersion, and ecosystem dynamics. As a memory aid, we can use FLUID: **F**low, **L**aminar, **U**sed in design, **I**n environment, **D**eterminer of turbulence! This helps us remember its expansive applications!
Always remember, recognizing the significance of Re can lead engineers to design better systems, increasing efficiency and safety across various fields.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Reynolds number is a crucial dimensionless parameter in fluid mechanics that quantifies flow characteristics. It helps determine whether a flow will be laminar or turbulent, thereby influencing appropriate modeling techniques and real-world applications.
Detailed
Reynolds Number
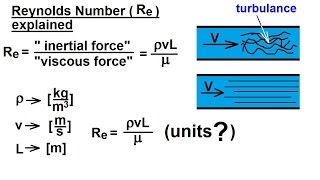
The Reynolds number (Re) is a dimensionless figure used extensively in fluid mechanics to predict flow patterns in different fluid flow situations. It is defined as the ratio of inertial forces to viscous forces and plays a critical role in identifying the nature of fluid flow—be it laminar or turbulent. The formula for calculating Reynolds number is:
$$Re = \frac{\rho u L}{\mu}$$
Where:
- $\rho$ = density of the fluid,
- $u$ = mean flow velocity,
- $L$ = characteristic length (such as diameter of a pipe),
- $\mu$ = dynamic viscosity of the fluid.
Generally, flows with Reynolds numbers less than 2000 are considered laminar, and those greater than 4000 are typically turbulent. Understanding the Reynolds number enables engineers and scientists to predict and model flow behavior in a variety of applications, enhancing design and operational efficiency in fields ranging from civil engineering to aeronautics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Reynolds Number
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Reynolds number (Re) is a dimensionless quantity used in fluid mechanics to predict flow patterns in different fluid flow situations. It is defined as the ratio of inertial forces to viscous forces and is given by the formula Re = (ρ * U * L) / μ, where ρ is the fluid density, U is the characteristic velocity, L is the characteristic length, and μ is the dynamic viscosity.
Detailed Explanation
The Reynolds number helps determine whether the fluid flow will be laminar or turbulent. Laminar flow occurs when Re < 2000, characterized by smooth and orderly fluid motion. Turbulent flow occurs when Re > 4000, marked by chaotic and irregular fluid motion. Understanding where a flow condition falls within this range is crucial for predicting how fluids will behave in different scenarios.
Examples & Analogies
Imagine a calm river flowing steadily compared to a stormy river. In the calm scenario (laminar flow), the water flows in layers, moving smoothly. In contrast, when the stormy river churns and splashes (turbulent flow), it becomes chaotic and unpredictable. The Reynolds number helps us measure these changes in flow behavior.
Importance of Reynolds Number
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Reynolds number is essential in characterizing flows, enabling engineers to design systems, predict system performance, and provide insights into fluid behaviors. By knowing the Reynolds number, one can infer the type of flow and its associated characteristics.
Detailed Explanation
Engineers and scientists use the Reynolds number to ensure systems operate optimally. For example, in pipe design, if the flow is too turbulent (high Reynolds number), it may lead to increased drag and pressure losses, which can affect the efficiency of a pump. Conversely, if the flow is laminar across a system that should ideally be turbulent, the mixing and heat transfer could be insufficient, resulting in poor performance.
Examples & Analogies
Think of Reynolds number as a speed limit for cars in a traffic system. If cars go too slow (laminar flow), they'll clog up the road. If they drive too fast (turbulent flow), they may crash. Engineers must find the right balance—much like determining the correct Reynolds number for pipes or ducts to ensure smooth fluid movement.
Calculating Reynolds Number
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To calculate Reynolds number, use the formula Re = (ρ * U * L) / μ. Identify the fluid's density (ρ), characteristic velocity (U), characteristic length (L), and dynamic viscosity (μ) from reference tables or measurements. All values need to be consistent; ensure units align properly, usually within the metric system.
Detailed Explanation
Finding each component required for the Reynolds number is straightforward but critical for accurate calculations. Fluid density and viscosity can often be looked up in standard reference materials. In real-world scenarios, engineers will select L based on the application—such as the diameter of a pipe or the length of a surface over which the fluid flows. Once the necessary values are plugged into the equation, the resulting number helps categorize the expected flow regime.
Examples & Analogies
Imagine you are a chef following a recipe. Each ingredient (fluid properties) needs to be measured accurately (correct values). The right combination (calculated Reynolds number) will lead to a successful dish (predictable fluid flow), while any incorrect measurement might ruin the recipe—just as incorrect Reynolds calculations could result in poor system design.
Applications of Reynolds Number
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Reynolds number has various applications across engineering fields, including aviation, automotive design, hydraulic systems, and even meteorology. By understanding Reynolds number, engineers can shape designs, improve efficiency, and predict flow-related challenges.
Detailed Explanation
In aviation, the Reynolds number helps predict how air flows over wings, influencing aerodynamics and performance. Similarly, in automotive engineering, it plays a key role in fuel efficiency calculations as air and water interact with cars. In fluid systems, it indicates how fluids behave and informs design decisions related to pipes, pumps, and other components.
Examples & Analogies
Think of Reynolds number as a weather forecast for fluid behaviors. Just as meteorologists use data to predict rain or sunshine, engineers use Reynolds number to anticipate flow issues and make necessary adjustments. This predictive ability ensures vehicles are efficient, aircraft fly correctly, and structures withstand critical forces.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Reynolds Number: Key to understanding flow characteristics under varying conditions.
-
Laminar Flow: Occurs at low Reynolds numbers, characterized by smooth streamlines.
-
Turbulent Flow: Occurs at high Reynolds numbers, involving chaotic fluid movements.
-
Dynamic Viscosity: Important factor influencing flow behavior.
-
Application in Engineering: Essential in designing systems for fluid transport and aerodynamics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A water flow in a pipe measuring 0.1 m in diameter with a velocity of 1 m/s has a Reynolds number indicating turbulent flow.
-
In an aviation context, engineers calculate Reynolds number to optimize wing shapes for better aerodynamic performance.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Reynolds number brings the flow, predicts if it’s steady or if it’ll go.
📖 Fascinating Stories
-
Imagine a river: calm and smooth in the morning (laminar) but wild and fast during a storm (turbulent). The Reynolds number helps us choose the right boat for each scenario.
🧠 Other Memory Gems
-
DUM-VD helps remember: Density, Velocity, Viscosity, Diameter.
🎯 Super Acronyms
Use RAIN
- **R**eynolds
- **A**pplications in fluid dynamics
- **I**nteresting flow distinctions
- **N**ature of laminar vs turbulent.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Reynolds Number
Definition:
A dimensionless quantity used to predict flow patterns in different fluid flow situations, defined as the ratio of inertial forces to viscous forces.
-
Term: Laminar Flow
Definition:
A type of flow in which fluid moves in smooth, orderly layers with minimal disruption.
-
Term: Turbulent Flow
Definition:
A type of flow characterized by chaotic changes in pressure and flow velocity.
-
Term: Dynamic Viscosity
Definition:
A measure of a fluid's internal resistance to flow, typically expressed in units of Pa·s.
-
Term: Inertial Forces
Definition:
Forces associated with the mass of a fluid that cause it to resist changes in velocity.
-
Term: Viscous Forces
Definition:
Forces that resist the motion of fluid layers sliding past each other.