Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Boundary Layers
Unlock Audio Lesson
Good morning, class! Today, we are diving into the topic of boundary layers, particularly looking at how they form over flat plates. Can anyone tell me why we need to study boundary layers in fluid flow?
I think they affect how fluids behave when they flow over surfaces, right?
That's correct, Student_1! The flow behavior is crucial for applications in engineering, especially when it comes to drag forces on vehicles or profiles. Now, what do we call the thin region where the effects of viscosity are significant?
The boundary layer!
Exactly! Remember the acronym 'BL' for Boundary Layer, which helps us keep track of this concept.
Boundary Layer Equations
Unlock Audio Lesson
Now let's look at the equations governing the boundary layers. Can someone remind us about the conservation equations we use?
We use mass conservation and momentum equations!
Correct! The mass conservation relates to the divergence of velocity, while the momentum equations deal with the forces acting on fluid elements. Can anyone state the expression for the mass conservation equation?
It's del u by del x plus del v by del y equals zero.
Great job! An easy way to memorize this is: 'Mediating in U and V leads to none,' which plays on the idea of maintaining balance in flow. These equations help us analyze flow in the boundary layer.
Displacement and Momentum Thickness
Unlock Audio Lesson
Let’s shift gears to two critical concepts: displacement thickness and momentum thickness. Why do you think these are important?
I guess they help us to understand how the boundary layer affects flow and pressure distribution?
Absolutely! Displacement thickness measures how much area is effectively 'displaced' by the boundary layer, which alters the flow field. Can anyone explain how we calculate displacement thickness?
Isn't it based on integrating the velocity profile across the boundary layer?
Yes! The formula integrates the velocity deficit across the boundary layer. To remember this, think of the acronym 'DPT,' where 'D' stands for Displacement, 'P' for Profile, and 'T' for Thickness.
Applications and Numerical Solutions
Unlock Audio Lesson
Now, let’s consider real-world applications. How do you think boundary layer theory plays a role in wind tunnel design?
It helps in ensuring that the flow remains laminar for accurate measurements!
Exactly! Thus, knowing the thickness of the boundary layer allows engineers to design better wind tunnels. Can anyone relate this to numerical methods?
We can solve the boundary layer equations using numerical techniques, which make it easier than manual calculations!
Well said! Modern computational fluid dynamics (CFD) simplifies these equations significantly, so remember 'CFD' as a tool that complements our physical understanding!
Concluding Thoughts
Unlock Audio Lesson
As we wrap up, can anyone summarize the key points we've discussed about boundary layers?
We learned about the importance of boundary layers, the governing equations, and key concepts like displacement and momentum thickness.
And how they're applied in designing wind tunnels and using numerical methods for solutions!
Fantastic, everyone! Remember that boundary layers, captured cleverly through equations and concepts, are fundamental to fluid dynamics!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section covers the fundamental aspects of flat plate boundary conditions, involving the derivation and numerical solutions of boundary layer equations for laminar flow. It further introduces significant terms such as displacement thickness and momentum thickness, explaining their implications in fluid mechanics and how they contribute to understanding boundary layer behavior in practical scenarios such as wind tunnels.
Detailed
In this section, we delve deep into the boundary layer approximations fundamental to fluid mechanics, particularly as it pertains to flat plates. The discussion begins with the derivation of the mass conservation and linear momentum equations relevant to boundary layers. Special emphasis is placed on the laminar flow conditions observed near flat surfaces. Key concepts such as displacement thickness, which quantifies the deflection of streamlines due to the presence of a boundary layer, and momentum thickness, which signifies the change in momentum within the boundary layer, are introduced. Practical implications of these concepts are highlighted through examples, including their application in the design of wind tunnels. The section concludes with insights into how modern computational techniques have simplified boundary layer analysis compared to historical methods. Overall, it frames the boundary layer concept within the larger context of fluid dynamics, illustrating both theoretical and practical aspects.
Youtube Videos
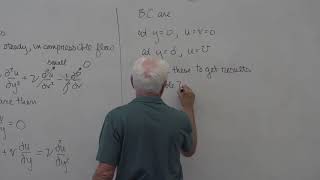
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Boundary Layers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We are talking about laminar boundary layers equations okay. So as you remember it the boundary layer equations what we derive it first is the mass conservation which is very simple as again I am repeating it for two-dimensional incompressible flow velocity divergence which is equal to del u by del x del v by del y.
Detailed Explanation
In this chunk, we discuss the fundamental concepts of laminar boundary layers. We start with the boundary layer equations, focusing on the mass conservation principle in fluid dynamics. This principle states that, in a fluid flow, the rate of mass entering a system must equal the rate of mass leaving the system. Mathematically, for two-dimensional incompressible flow, this is represented as the divergence of the velocity vector being equal to zero. In simpler terms, it entails that if the fluid enters a certain area, it must also leave it, maintaining a balance.
Examples & Analogies
You can think of mass conservation like water flowing through a garden hose. If you have water flowing in one end of the hose, the same amount of water must exit at the other end. If you were to pinch the hose, water would build up, illustrating how the flow cannot be maintained unless there is an equal output.
Simplification for Boundary Layer Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
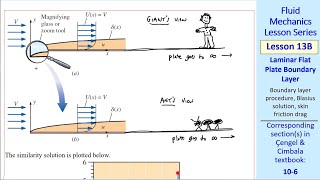
So if you look at that this is a parabolic equations which simplified us just trying to sketch that part okay. So that means if I have a wall surface like this and you have a formations of boundary layers, that is what is sigma x.
Detailed Explanation
Here we introduce the parabolic nature of boundary layer equations, simplifying the complex behavior of fluid near a wall. The boundary layers are formed due to interaction between fluid flow and solid surfaces, like a flat plate in this example. As the fluid flows past the plate, a layer close to the surface has its velocity reduced due to the no-slip condition (where fluid sticks to the wall). This results in a thickness of fluid that does not move as fast as the rest of the fluid, forming what we call the boundary layer, and we find that these equations take on a parabolic form, which allows for simpler calculations than the original complex Navier-Stokes equations.
Examples & Analogies
Imagine putting your hand out of the window of a moving car. The air hitting your hand is fast, but the air closest to your hand (the boundary layer) is moving much slower because it sticks to your skin. This illustrates the concept of a boundary layer where the fluid velocity decreases as you get closer to the boundary (your hand).
Boundary Conditions in Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So that means if I take a control volumes, I know these boundary conditions at the wall is the u v both are 0 that is the non-slip boundary conditions.
Detailed Explanation
In this section, we address the boundary conditions essential for solving fluid flow problems. The no-slip condition, which states that the velocity of a fluid at the boundary is zero (u = 0, v = 0), is crucial. This means that the fluid at the very surface of the plate does not move; it is 'stuck' to the plate. This condition is fundamental in analyzing how the fluid behaves as it flows past objects, and it allows us to mathematically define how the flow develops from the wall into the free stream.
Examples & Analogies
A real-world analogy would be to think of a layer of syrup on the bottom of a plate. The syrup rests motionless at the plate's surface, demonstrating the no-slip boundary condition, while the layer above it moves freely at a different speed.
Numerical Solutions and Computational Techniques
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So by solving these equations today is very easy because you have a very high computing techniques systems with us and there are lot of numerical techniques are developed it to approximate even if Navier-Stokes equations.
Detailed Explanation
This chunk discusses the advancements in computational fluid dynamics (CFD) that have made solving boundary layer equations simpler and more efficient. With modern computing power, techniques such as finite difference and finite volume methods allow engineer to simulate fluid dynamics problems that were previously solvable only through laborious hand calculations. As a result, engineers can explore complex geometries and fluid behaviors quickly and analyze results in detail.
Examples & Analogies
Think of how you use a calculator to quickly find the result of complex math problems rather than solving them by hand. Similarly, researchers and engineers use computers to address fluid dynamics problems that would take an enormous amount of time to solve manually.
Displacement Thickness Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look it, another concept what we look it called a displacement thickness. The basically as we know it the boundary layer thickness developments happens it okay.
Detailed Explanation
Displacement thickness is a critical parameter derived from boundary layers that indicates how the flow is affected by the presence of a boundary (like a plate). It represents the 'apparent' thickness added to the body due to the presence of the boundary layer, which effectively displaces the streamline further away from the surface than it would be if there were no boundary layer present. We compute displacement thickness by assessing the reduction in mass flow due to slower velocities inside the boundary layer compared to the free stream.
Examples & Analogies
Imagine a swimming pool's water level being influenced by a swimmer. When the swimmer enters the water, their body disrupts the water surface and displaces the volume of water. In fluid dynamics, the displacement thickness is like that, showing how the layer of slower-moving fluid pushes the effective streamline of flow away from the plate.
Momentum Thickness in Thin Plates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we come to the momentum thickness which is not big the concept which is already we talk about shear stress displacement thickness.
Detailed Explanation
Momentum thickness is another important concept that provides insights into the momentum deficit within a boundary layer. It represents the thickness of an imaginary layer of fluid that moves as if it were contributing to the same momentum as the actual layer. Momentum thickness helps in calculating the friction forces acting on the plate due to viscous effects of the boundary layer and is closely related to shear stress acting at the wall.
Examples & Analogies
Think of momentum thickness like a packed suitcase on a long journey. You are carrying not only the suitcase itself but also an imaginary weight that it represents. In fluid boundary layer terms, it provides insight into the effectiveness of the layer's momentum in relation to the forces acting on it.
Key Differences in Laminar and Turbulent Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we are not going to more details. When you go for the turbulent boundary layers just conceptually I will discuss with you.
Detailed Explanation
In this section, we introduce the differences between laminar and turbulent boundary layers. While laminar flow exhibits smooth and orderly movement, turbulent flow is chaotic and characterized by fluctuating velocities. The equations governing turbulent flow are more complex, requiring empirical data to model accurately. Although we focus on laminar flow in our calculations, understanding how turbulence fundamentally alters flow characteristics is vital for advanced fluid mechanics.
Examples & Analogies
Consider the difference between a calm stream and rapids. In the calm stream (laminar flow), the water flows smoothly and evenly. In contrast, the rapids (turbulent flow) are wild and chaotic, demonstrating how turbulent flow displays a wide range of velocities and behaviors. Understanding both flows helps engineers design more effective systems.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Boundary Layer: A critical region where effects of viscosity dominate.
-
Displacement Thickness: Represents the effective distance by which the flow is displaced due to the boundary layer.
-
Momentum Thickness: Indicates the drag associated with the boundary layer by measuring the momentum flux loss.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of displacement thickness could be evaluating airflow over a flat plate, which can be quantified through integration of velocity profiles.
-
In wind tunnel experiments, the knowledge of boundary layer thickness allows for precise calibration of instruments, ensuring data accuracy.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Boundary layer flows, sweet as a song, viscosity shows where effects belong.
📖 Fascinating Stories
-
Imagine a calm lake rippling as a gentle breeze brushes the surface, this is like laminar flow. However, when the wind picks up and water splashes wildly, that's turbulent flow.
🧠 Other Memory Gems
-
Remember 'DPT' (Displacement, Profile, Thickness) when calculating displacement thickness in flow.
🎯 Super Acronyms
Use 'BL' to easily recall Boundary Layer, the key region that influences fluid behavior near surfaces.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Boundary Layer
Definition:
A thin region near the surface of an object where viscous effects are significant.
-
Term: Displacement Thickness
Definition:
A measure of the distance by which the wall of an object is effectively displaced due to the presence of a boundary layer.
-
Term: Momentum Thickness
Definition:
A measure of the loss of momentum flux in the boundary layer, quantifying drag.
-
Term: Reynolds Number
Definition:
A dimensionless number that helps predict flow patterns in different fluid flow situations.
-
Term: Laminar Flow
Definition:
A type of flow where fluid moves in parallel layers with no disruption between them.
-
Term: Turbulent Flow
Definition:
A type of flow characterized by chaotic changes in pressure and flow velocity.