Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Boundary Layer Equations
Unlock Audio Lesson
Today we start with the concept of boundary layer equations derived from the Navier-Stokes equations. Can anyone tell me what these equations model?
They model the motion of fluid substances.
Correct! Specifically, we focus on flow past a flat plate under steady and incompressible conditions. The equations simplify in this context. Can you recall the main type of flow we are discussing?
Laminar flow.
Exactly! Laminar flow occurs at low Reynolds numbers. In this section, we will explore methods to numerically solve these equations.
Displacement and Momentum Thickness
Unlock Audio Lesson
Let’s discuss displacement thickness first. Can anyone explain what it represents in fluid dynamics?
Isn't it the distance a streamline is deflected due to the boundary layer?
Great! It's the deflection caused by the boundary layer formations. Now, how does this relate to momentum thickness?
Momentum thickness is a measure of the momentum deficit in the boundary layer.
Correct! Remember, both thicknesses help us understand how the overall flow is affected by laminar boundary layers.
Numerical Techniques in Solving Boundary Layer Equations
Unlock Audio Lesson
Now, can someone explain why numerical techniques are advantageous in boundary layer analysis?
They allow us to solve complex equations that would be very difficult to calculate by hand.
Exactly! With advancements in computing, we can utilize computational fluid dynamics to find approximate solutions for complex geometries and conditions.
So, can we apply these techniques to turbulent flows too?
Yes, but turbulent flows are much more complex. Understanding laminar flows sets a good foundation before tackling turbulence.
Historical Context and Contributions
Unlock Audio Lesson
Who can name some of the early contributors to the boundary layer theory?
Prandtl and his students, like Blasius!
That's correct! Their work in the late 19th and early 20th centuries paved the way for our current understanding. They used simpler methods back then, without computers.
So their methods were rudimentary compared to what we have now?
Yes, but they laid the foundation that allows us to use sophisticated computational methods today.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into numerical techniques used for solving laminar boundary layer equations. It also introduces concepts like displacement thickness and momentum thickness, along with historical contributions to boundary layer theory.
Detailed
Numerical Solutions of Laminar Boundary Layers
This section focuses on the numerical solutions to the laminar boundary layer equations, which are derived from the Navier-Stokes equations under simplified assumptions for steady, incompressible flow. The key contributions from early researchers such as Prandtl and his students are highlighted, along with the significance of numerical techniques in modern fluid mechanics. The concepts of displacement thickness and momentum thickness are introduced as critical aspects of boundary layer analysis, which quantify the effects of the boundary layer on flow dynamics. The section explains how to solve these equations using numerical techniques, emphasizing the practicality of computational fluid dynamics (CFD) in obtaining velocity distributions, shear stress, and other parameters in laminar boundary layers.
Youtube Videos
![Laminar boundary layers [Fluid Mechanics #13]](https://img.youtube.com/vi/gTtBiMNoofY/mqdefault.jpg)
![[Fluid dynamics: Boundary layer theory] Laminar Boundary Layer, Part 2](https://img.youtube.com/vi/60ySpFpu7yo/mqdefault.jpg)
![[Fluid dynamics: Boundary layer theory] Laminar Boundary Layer, Part 1](https://img.youtube.com/vi/Fb_TlVZObQw/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Laminar Boundary Layers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So basically we are talking about laminar boundary layers. To getting these solutions we are just looking at some simplifications as we did it for earlier case that we are looking at the uniform speed flow v is going that is what is the free stream velocity and if you look at the sketch the same and very thin plates okay this is thin plate thin plate because this is to be simplify the conditions that we can get a solutions for this.
Detailed Explanation
In this chunk, the discussion begins by introducing the concept of laminar boundary layers. A laminar boundary layer forms when the fluid flows over a surface, such as a flat plate. The flow is smooth and orderly, characterized by layers of fluid that slide past one another. To analyze this type of flow, we make some simplifications, particularly assuming a uniform speed of flow, referred to as the free stream velocity. By analyzing thin plates, we simplify the conditions, making it easier to obtain mathematical solutions for the flow characteristics within the boundary layer.
Examples & Analogies
Imagine a smooth, calm river flowing over a flat rock. Just like the calm flow of the water that gently moves over the rock, in a laminar flow over a flat plate, the layers of water slide past each other without much turbulence.
Boundary Layer Thickness and Reynolds Number
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And basically we are looking at what could be the boundary layer thickness if the free stream velocity is u okay. And considering it is that the boundary layers whatever is here it remains as a laminar boundary layers that means it is a lesser than the critical Reynolds numbers which earlier I said it should be less than 1 log 10 to the power 5 okay.
Detailed Explanation
Boundary layer thickness is a critical concept in fluid mechanics, particularly for laminar flows. It represents the region adjacent to the surface where the effects of viscosity are significant. In this context, the critical Reynolds number is vital - a threshold that indicates whether the flow remains laminar. If the Reynolds number, which combines factors like fluid speed, density, and viscosity, is less than approximately 100,000 (or 1 log 10^5), then we can confidently say that the flow within the boundary layer remains laminar.
Examples & Analogies
Think of the critical Reynolds number like the threshold between calm and turbulent water. Below a certain speed (just like a low Reynolds number), water flows smoothly past your hand; above that speed, the water becomes more chaotic and turbulent.
Numerical Techniques in Solving Boundary Layer Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So today is very easy because you have a very high computing techniques systems with us and there are lot of numerical techniques are developed it to approximate even if Navier-Stokes equations.
Detailed Explanation
With modern computational technology, solving the boundary layer equations has become significantly easier compared to the past when these were solved by hand. The use of numerical techniques allows us to approximate solutions to the Navier-Stokes equations, which govern fluid motion. Through various numerical methods, we can efficiently analyze how fluids behave near surfaces, determine the velocity profiles within the boundary layer, and predict important characteristics like drag and shear stress.
Examples & Analogies
Consider how weather forecasting has evolved. In the past, meteorologists used paper charts to predict weather patterns. Today, they rely on supercomputers that simulate weather models, delivering accurate forecasts—a bit like how numerical techniques help us solve fluid problems.
Displacement Thickness and Momentum Thickness
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
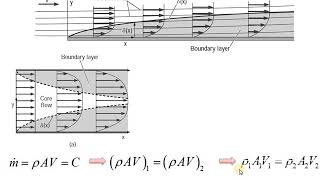
Now if you look at more details if I looking it from the edge of a plate as I go and if I sketch the boundary velocity distributions this is what the boundary layers. Okay this is what the boundary layers if I sketch the velocity distributions you can see that the tangent and this velocity distribution at the y which is a representing us the wall shear stress.
Detailed Explanation
Displacement thickness and momentum thickness are important metrics for characterizing laminar boundary layers. Displacement thickness describes how much the actual flow 'feels' thicker due to the presence of the boundary layer; it quantifies how much mass flow is reduced due to viscous effects. Momentum thickness, on the other hand, relates to the change in momentum within the boundary layer and is crucial for calculating drag forces. Both measures help engineers design better aerodynamic shapes by understanding fluid behavior around surfaces.
Examples & Analogies
Think of displacement thickness like the shadow of a tree that extends beyond its physical trunk. The shadow represents the area affected by the tree, just as the boundary layer affects the flow of fluid despite the physical thickness of the layer being much smaller.
Calculating Boundary Layer Properties
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The same way also he estimate it what will be the wall stress okay that is what you know it that what we can get it if you know this velocity gradient mu times at y equal to 0.
Detailed Explanation
To understand the effects of boundary layers, we need to study wall stress, often referred to as shear stress, which occurs at the fluid-solid interface. By analyzing the gradient of velocity at the wall (y = 0), we can calculate the shear stress using the viscosity of the fluid. These calculations allow us to determine how fluid adhesion affects drag forces and can help in predicting performance in applications like aircraft wings or ship hulls.
Examples & Analogies
Imagine pushing your hand through thick syrup. The syrup sticks to your hand, requiring force to move it through. This 'stickiness' represents the wall shear stress at the interface between the syrup and your skin, analogous to the wall shear stress in fluid mechanics.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Boundary Layer: The thin region close to a solid surface where viscosity affects the flow.
-
Displacement Thickness: The measure of how much outer streamlines are pushed away due to the boundary layer.
-
Momentum Thickness: Represents the mass and momentum deficit in a flow due to the boundary layer.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a wind tunnel, the boundary layer forms along the walls, influencing the flow patterns and drag forces.
-
When analyzing flow past a flat plate, numerical methods can determine the velocity distribution across the boundary layer.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In layers smooth, like silk through the night,
📖 Fascinating Stories
-
Imagine a river flowing past a stone. The water near the stone slows down, creating a ‘slow zone’—this is like the boundary layer in fluid dynamics.
🧠 Other Memory Gems
-
Remember D for Deflection (Displacement Thickness) and M for Momentum (Momentum Thickness).
🎯 Super Acronyms
Use the acronym DMM - where D is Displacement, M for Momentum, and the last M for the measure, to recall their functions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Boundary Layer
Definition:
A thin region adjacent to a solid surface where viscous effects are significant.
-
Term: Displacement Thickness
Definition:
The distance by which the outer streamlines are deflected due to the presence of a boundary layer.
-
Term: Momentum Thickness
Definition:
The thickness that quantifies the momentum deficit in the boundary layer.
-
Term: Reynolds Number
Definition:
A dimensionless quantity that helps predict flow patterns in different fluid flow situations.
-
Term: Laminar Flow
Definition:
A type of fluid motion in which the fluid moves in smooth, parallel layers.
-
Term: Numerical Techniques
Definition:
Approaches used to solve mathematical models through numerical approximation methods.