Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Complex Exponential Function
Unlock Audio Lesson
Today, we're diving into the complex exponential function, defined as e^z = e^(x + iy) = e^x(cos(y) + i sin(y)). Can anyone tell me what the x and y represent here?
I think x is the real part, and y is the imaginary part!
Exactly! The real part x determines the growth or decay, while the imaginary part y defines the oscillation. From this perspective, how would you interpret the mapping in the complex plane?
Isn’t it like drawing spirals since it has both magnitude and angle?
Correct! The function indeed maps spirals in the complex plane, exhibiting the essence of harmony between growth and oscillation.
Properties of Complex Exponential Function
Unlock Audio Lesson
Let’s look into some important properties of the complex exponential function. For instance, we have the addition rule, |e^z| = e^x, and its periodic nature. What do we think happens to e^z when we add 2πi?
It would remain the same because of periodicity!
Right! Since e^(z + 2πi) returns to its original form, this depicts intrinsic periodic behavior, very useful in engineering contexts. Remember this acronym: "APM" for Addition, Modulus, Periodicity.
APM – Addition, Modulus, Periodicity. Got it!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the definition and properties of the complex exponential function, emphasizing its significance in engineering applications. The function connects the real and imaginary components of complex numbers and demonstrates crucial behaviors in oscillations and waves, pertinent to civil engineering contexts.
Detailed
Detailed Summary
The complex exponential function is defined for a complex number z = x + iy as:
$$ e^z = e^{x+iy} = e^x (cos(y) + i sin(y)) $$
This formulation indicates that the real part, x, influences the magnitude of the function while the imaginary part, y, governs the oscillation (angle) within the complex plane. Consequently, this function reveals spirals that manifest in the complex plane, elucidating both growth/decay and rotation phenomena. The properties of the complex exponential function are numerous and serve critical purposes in both mathematics and engineering, particularly in solving differential equations and analyzing signals.
Youtube Videos
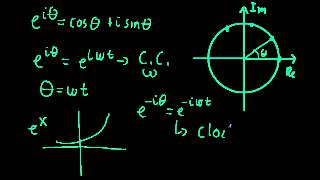
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Complex Exponential Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The exponential of a complex number z = x + iy is defined as:
$$ e^z = e^{x + iy} = e^x ( ext{cos} y + i ext{sin} y ) $$
Detailed Explanation
The complex exponential function extends the concept of the exponential function to complex numbers. When we have a complex number expressed as z = x + iy, where x is the real part and y is the imaginary part, we can express the exponential function of z using the formula above. This formula combines the real exponential function, e^x, with the trigonometric components involving cosine and sine. Essentially, the exponential part, e^x, controls the scaling or magnitude of the output, while the terms cos(y) and sin(y) dictate the direction of the output in the complex plane.
Examples & Analogies
Think of the complex exponential function like navigating on a map. The real number, x, represents how far you walk in a straight line (the magnitude), while y represents the angle or direction in which you're heading. By combining both, you're able to determine your exact position on the map.
Key Points of the Complex Exponential Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- The real part x controls the magnitude (growth/decay),
- The imaginary part y determines the oscillation (angle/rotation),
- This function maps spirals in the complex plane.
Detailed Explanation
The complexity of the exponential function arises from its relationship with both real and imaginary components. The real part, x, influences how fast the value grows or shrinks; for example, larger values of x lead to larger outputs. Conversely, the imaginary part, y, contributes to oscillatory behavior, affecting how the output value rotates around the origin of the complex plane. When you visualize this, the outputs form spirals: as x increases, the points rotate around the center at angles determined by y.
Examples & Analogies
Imagine a Ferris wheel. The height you achieve at any moment corresponds to the real part (x), while the angle at which you are riding (your position around the wheel) corresponds to the imaginary part (y). As the wheel spins (your angle shifts), you move up and down (magnitude changes), creating a spiral path in the air as you ride.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Complex Exponential Function: Bridges growth and oscillation in complex analysis.
-
Euler's Formula: Connects complex exponentials to trigonometric functions.
-
Magnitude and Oscillation: The role of real and imaginary parts in defining behavior in the complex plane.
-
Properties: Key properties such as addition rule and periodic nature are foundational to understanding complex functions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The complex exponential function defines spirals in the complex plane, useful in vibrational analysis.
-
The addition rule of the complex exponential function simplifies calculations in electrical engineering problems.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Complex Exponential Function
Definition:
A function defined for complex numbers, represented as e^(x + iy) = e^x(cos(y) + i sin(y), where x is the real part and y is the imaginary part.
-
Term: Magnitude
Definition:
The absolute value or distance of a complex number from the origin in the complex plane.
-
Term: Oscillation
Definition:
The repetitive variation of a quantity, which in this case is represented by the imaginary part of the complex exponential.
-
Term: Periodic Function
Definition:
A function that repeats its values at regular intervals, exemplified by the complex exponential function.
-
Term: Addition Rule
Definition:
A property of the complex exponential function stating that e^(z1 + z2) = e^(z1) * e^(z2).