Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Definition of Complex Powers
Unlock Audio Lesson
Today, we will discuss complex powers. Specifically, if we have a complex number expressed as z = re^(iθ), how do you think we calculate its nth power?
I think we raise the modulus to the power n and multiply the angle by n.
Exactly! The definition for complex powers is z^n = r^ne^(inθ). This shows how the absolute value and angle of the complex number transform when elevated to a power.
So, it changes the way we visualize it too?
Good question! Yes, it affects the spiral nature we observe in the complex plane, reinforcing our visual understanding.
Is that similar to rotating vectors?
Absolutely! The rotation becomes clearer when we visualize these powers. Let's remember: 'Magnitude up, Angle multipliers up' for this concept.
To summarize, in complex powers, we raise the modulus to n while multiplying the angle by n.
Definition of Complex Roots
Unlock Audio Lesson
"Now let's look at complex roots! We express nth roots of a complex number like this: $
Application in Civil Engineering
Unlock Audio Lesson
Now, let’s connect what we learned about complex powers and roots to civil engineering applications. Can anyone explain how these concepts help in analyzing structures?
I believe they help in modal analysis. The roots and powers translate to different vibration modes of a structure?
Exactly! The analysis of resonance frequencies often draws from the roots of complex numbers. When you model dynamic responses of structures, these roots inform us about oscillation behaviors.
So it's essential for knowing how structures react to forces, like during an earthquake?
Right! And understanding the periodic nature of these vibrations is crucial for safety in engineering designs.
To sum up, complex powers and roots empower us to predict behaviors in civil engineering through modal analysis and resonance frequencies.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we define complex powers and roots of complex numbers and discuss their geometric interpretation in the complex plane. Applications in civil engineering, including modal analysis and resonance frequency analysis, are also highlighted.
Detailed
Detailed Summary
In the study of complex numbers, the concepts of complex powers and roots play a crucial role. Given a complex number expressed in polar form as $z = re^{iθ}$, its complex power is defined as:
$$z^n = r^ne^{inθ$$
This means the absolute value of the complex number raised to the power $n$ affects the magnitude, while the angle gets multiplied by $n$.
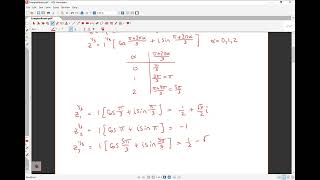
For exploring the roots of complex numbers, the nth roots can be expressed as:
$$\sqrt[n]{z} = r^{1/n}e^{(θ + 2kπ)/n}, \quad k = 0, 1,..., n-1$$
Geometrically, the nth roots of a complex number are positioned evenly on a circle in the complex plane, forming the vertices of a regular polygon. This aspect is particularly relevant in civil engineering, where understanding the dynamics of complex roots assists in areas such as modal analysis of structures and analysis of resonance frequencies in mechanical systems.
Youtube Videos
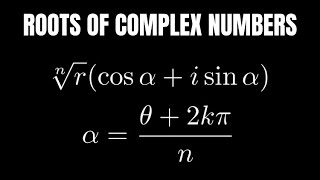
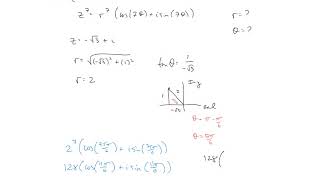
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Complex Powers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Given a complex number z = re^(iθ), we define its complex power as:
z^n = r^n e^(inθ)
Detailed Explanation
To understand complex powers, we start with a complex number in polar form, expressed as z = re^(iθ). Here, 'r' represents the modulus (or length) of the complex number, and 'θ' is the argument (the angle). When we take the nth power of z, we raise both the modulus and the exponential part:
- The modulus is raised to the power of 'n', yielding r^n.
- The exponential part multiplies the angle by 'n', resulting in e^(inθ). Thus, the formula z^n = r^n e^(inθ) captures how both the magnitude and the angle change in the complex plane as we raise a complex number to an integer power.
Examples & Analogies
Imagine a wind turbine spinning in a circular path. The distance from the center of the turbine to the blade tip represents the modulus (r), while the angle at which the blade is positioned from a reference line represents the argument (θ). If we were to model the turbine’s rotation at different speeds, we could think of the nth power as simulating multiple blades operating at different angles yet all maintaining the same radius. Just as raising the turbine's power impacts how fast it spins, exponentiating a complex number changes both the distance and orientation from the origin.
Definition of Complex Roots
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Similarly, the nth roots of a complex number are given by:
√n z = r^(1/n) e^(i(θ + 2kπ)/n), k = 0, 1, ..., n-1
Detailed Explanation
Calculating the nth roots of a complex number is somewhat the reverse of finding its power. From the expression √n z = r^(1/n) e^(i(θ + 2kπ)/n), we see that we are returning to the original modulus:
- The modulus is taken to the nth root, giving us r^(1/n).
- The angle θ is divided by 'n', with an additional term, 2kπ/n, allowing us to find all 'n' unique roots. Each value of 'k' (0 to n-1) provides a different angle and hence a different root, which means there are 'n' distinct roots evenly spaced on a circle in the complex plane.
Examples & Analogies
Consider a pizza sliced into equal parts, where each slice represents a root of the complex number. If the pizza has a radius representing the modulus (r), then each slice placed on a table (the complex plane) corresponds to a unique angle derived from θ divided by n. Just like how each slice maintains the same radius but points in a different direction, each root of the complex number points out from the origin at evenly spaced intervals.
Geometric Interpretation of Roots
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Geometric Interpretation:
- The n roots lie evenly spaced on a circle of radius r^(1/n) in the complex plane.
- They form the vertices of a regular polygon.
Detailed Explanation
The geometric interpretation of complex roots provides a visual understanding that complements the algebraic method. When plotting the nth roots of a complex number on the complex plane, the roots appear distributed evenly along the circumference of a circle with a radius of r^(1/n). Each root represents a vertex of a regular n-sided polygon, reflecting how the roots relate to each other in angles and distances from the origin. This method not only helps in visualizing complex mathematics but also simplifies understanding how these roots behave when subjected to additional transformations.
Examples & Analogies
Think of a bicycle wheel where each spoke represents a root of a complex number. When you divide the wheel into equal segments (just like calculating the nth roots), each spoke points toward a unique direction, yet all maintain the same distance from the center. As you rotate the wheel, you visualize how each root 'spins' around the origin but remains evenly spaced, demonstrating the harmony between algebra and geometry in complex numbers.
Applications in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Application in Civil Engineering:
- Used in the modal analysis of structures.
- Helps analyze resonance frequencies in mechanical systems.
- Relevant in dynamic response modeling of damped/undamped systems.
Detailed Explanation
In civil engineering, the principles of complex powers and roots are critical during the analysis and design of structures. When evaluating how structures respond to forces, engineers use the modal analysis to understand different vibration modes that structures may exhibit. By applying complex powers and finding roots, engineers can calculate the natural frequencies at which structures resonate, ensuring they design buildings and bridges that can withstand dynamic loads without leading to excessive vibrations or potential failure.
Examples & Analogies
Consider a suspension bridge swaying in the wind: each sway can be seen as a vibration mode. Just like a musician tunes a guitar string to find the best tone, engineers must tune the bridge's response to various forces, using complex roots to analyze the structure's potential oscillations. By understanding these complex behaviors, engineers can anticipate and mitigate issues, ensuring the safety and longevity of the bridge under various conditions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Definition of Complex Powers: Complex powers are calculated by raising the modulus to the power and multiplying the angle.
-
Definition of Complex Roots: Complex roots involve taking the modulus root and evenly spacing the angles around the unit circle.
-
Geometric Interpretation: Both powers and roots can be represented in the complex plane, providing visualization of transformations.
-
Application in Civil Engineering: Complex powers and roots are applied in modal analysis and understanding resonance frequencies.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For z = 2e^(iπ/4), z^3 can be calculated as (2^3)e^(3iπ/4) = 8e^(3iπ/4).
-
If z = 1 + i, express z in polar form and calculate the square root, resulting in √2 * e^(iπ/4).
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Powers and roots spin fine, magnitude up, angles align, evenly spaced in a circle's design.
📖 Fascinating Stories
-
Imagine a kingdom where knights represent complex numbers. When raised to a power, they strengthen their armor (magnitude) and conquer new lands (angle). When finding roots, they equally share their new territories, creating a polygonal kingdom!
🧠 Other Memory Gems
-
For powers, we say: "Mighty Angle Multiplies". For roots, "Regular Radius Shares".
🎯 Super Acronyms
P.A.R. — Powers (Magnitude up, Angle multiplied), And Roots (Radius down, Angles spaced).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Complex Powers
Definition:
The result of raising a complex number to an integer exponent, exhibiting a change in magnitude and angle.
-
Term: Complex Roots
Definition:
Values obtained by taking the nth root of a complex number, represented geometrically as points on a circle in the complex plane.
-
Term: Polar Form
Definition:
A way to express complex numbers with a modulus and an argument in the form z = re^(iθ).
-
Term: Geometric Interpretation
Definition:
Visual representation of complex numbers in the complex plane, highlighting their relationships.
-
Term: Modal Analysis
Definition:
A technique used to determine the natural vibration modes of a structure.
-
Term: Resonance Frequency
Definition:
The frequency at which a system naturally oscillates, important in analyzing dynamic systems.