Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Euler's Identity
Unlock Audio Lesson
Today, we're diving into how trigonometric functions relate to complex exponentials through Euler's identity. Can someone remind me what Euler's formula states?
It says that e^(ix) = cos(x) + i*sin(x).
Exactly! So, from this formula, we can derive how cos(x) and sin(x) can be expressed in terms of exponential functions. Let's write these identities down. Who can tell me the expression for cosine?
Cosine is cos(x) = (e^(ix) + e^(-ix)) / 2.
Great! And how about sine?
Sin(x) = (e^(ix) - e^(-ix)) / (2i).
Perfect! These transformations are very useful when we need to differentiate or integrate trigonometric functions. It makes our calculations a lot easier!
Let's summarize: we learned how trigonometric functions can be represented using complex exponentials, which aids in solving problems in complex analysis.
Applications of the Identities
Unlock Audio Lesson
Now that we understand the identities, can anyone think of practical applications for expressing trigonometric functions in terms of exponentials?
I guess it would help in signal processing, right?
Yes! It also helps in control systems and electrical engineering when analyzing alternating currents.
Exactly, you both are right! By transforming trigonometric functions into exponentials, we can work with complex signals more efficiently. Does anyone know any other fields where this is useful?
Maybe in mechanical vibrations?
Yes! The way we analyze vibrations and oscillations can greatly benefit from these transformations. To summarize, we explored how representing trigonometric functions as exponentials aids in various engineering applications.
Differentiation and Integration
Unlock Audio Lesson
Let’s discuss how using exponential forms influences differentiation and integration. Why would using Euler's identity make these operations easier?
Because differentiating e^(ix) is straightforward since the derivative is itself, while with trig functions, they involve more steps.
Exactly! When we differentiate or integrate sine and cosine directly, we have to remember their derivatives, but exponentials remain consistent. Let's take an example. What is the derivative of cos(x) using the identities?
If we use the identity, it would be -sin(x), but working with exponentials should lead to the same result.
Correct! We can prove that easily with Euler's identity. Using these transformations simplifies many calculus operations. In summary, we discussed how to differentiate and integrate trigonometric functions more efficiently using complex exponential forms.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The relationship between trigonometric functions and complex exponentials is articulated through Euler’s identity, allowing the transformation of trigonometric expressions into exponential forms. Such transformations are crucial for facilitating differentiation and integration in complex analysis and signal processing.
Detailed
Relationship with Trigonometric Functions
In this section, we explore how Euler's identity connects trigonometric functions with complex exponential functions. The essential identities derived from Euler’s formula state that:
- Cosine: $$\cos(x) = \frac{e^{ix} + e^{-ix}}{2}$$
- Sine: $$\sin(x) = \frac{e^{ix} - e^{-ix}}{2i}$$
These equations demonstrate how trigonometric expressions can be reformulated into exponential forms, significantly simplifying the processes of differentiation and integration within the fields of complex analysis and signal processing. Understanding this relationship enables engineers and mathematicians to utilize exponential forms in modeling oscillatory behaviors, thereby streamlining calculations and analyses in practical applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Euler’s Identities for Trigonometric Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
By Euler’s identity:
e^{ix} + e^{-ix} = 2 ext{cos}x,
e^{ix} - e^{-ix} = 2i ext{sin}x
Detailed Explanation
Euler’s identities link complex exponentials directly to trigonometric functions. The first identity shows that the sum of a complex exponential and its inverse results in a simple cosine function. Conversely, the second identity illustrates how the difference between a complex exponential and its inverse relates to the sine function. This alignment between complex exponentials and trigonometric functions simplifies the process of working with these equations in calculus.
Examples & Analogies
Think about how music can be represented in different forms. Just as a song can be expressed as notes on a sheet music (trigonometric functions) or as chords (complex exponentials), these identities allow us to switch between different forms seamlessly. This is why musicians often find it easier to manipulate chords because they can simplify the complexity involved in notes and rhythms.
Simplification of Trigonometric Expressions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These identities allow us to transform trigonometric expressions into exponential form, making them easier to differentiate or integrate in complex analysis or signal processing.
Detailed Explanation
Using Euler’s identities, we can convert trigonometric functions, which may be difficult to manipulate, into their exponential forms. This transformation is particularly useful in calculus, as derivatives and integrals of exponentials are simpler to work with than those of trigonometric functions. Thus, engineers and mathematicians often employ these identities when performing complex analysis or working on signal processing tasks.
Examples & Analogies
Imagine you are trying to solve a complex puzzle. Some pieces fit together nicely when viewed from one angle (trigonometric form), but when you rotate them (transforming to exponential form), they fit together much better. This rotation allows you to visualize and solve the puzzle more effectively, just as transforming expressions can help engineers and mathematicians solve problems more efficiently.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Euler's Identity: The connection between trigonometric functions and complex exponentials.
-
Complex Exponential Function: A function of a complex number leading to simplifications in calculus.
-
Trigonometric Transformations: The process of expressing trigonometric functions in exponential forms for easier analysis.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using Euler's formula to express sin(30 degrees) as e^(iπ/6).
-
Deriving the integral of cos(x) using its exponential representation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Euler's formula shines so bright, turns sin and cos to exponential light.
📖 Fascinating Stories
-
Imagine a mathematician who needed to simplify trigonometric calculations. He discovered that by using a magical identity, he could turn sine and cosine into more manageable exponential forms!
🧠 Other Memory Gems
-
Remember 'e' is for Euler, 'i' comes before 'sine', and together they make the perfect line!
🎯 Super Acronyms
E.C.T.
- Euler's formulas Connect Trigonometry!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Euler's Identity
Definition:
A formula that establishes the fundamental relationship between trigonometric functions and complex exponentials, defined as e^(ix) = cos(x) + i*sin(x).
-
Term: Complex Exponential Function
Definition:
A function of the form e^(z), where z is a complex number.
-
Term: Trigonometric Functions
Definition:
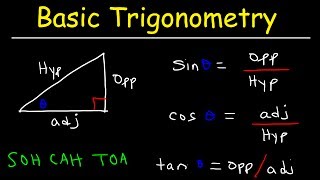
Functions such as sine, cosine, and tangent which relate the angles of a triangle to the ratios of its sides.