Logarithm of a Complex Number
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Complex Logarithm
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are going to explore the complex logarithm, which acts as the inverse of the complex exponential function. So, when we express a complex number in polar form, can anyone tell me what that looks like?

Isn’t it something like z = re^(iθ)?

Exactly! Now, if we apply the logarithm to this expression, what do we obtain?

We get ln(z) = ln(r) + iθ!

Correct! Now, notice the 'iθ' part. What's interesting about this term?

It can take on multiple values due to periodicity?

Yes! This is where the logarithm becomes multi-valued. So we can express it as ln(z) = ln(r) + i(θ + 2πn), where n is any integer. This means we could have infinitely many values!

That sounds complex—how do we decide which value to use?

Great question! We typically use the principal value, where θ is constrained to the interval (-π, π]. This makes calculations more manageable.

To sum up, we learned that the complex logarithm connects exponential behavior with trigonometric relationships. Let’s keep moving into its applications next!
Applications of Complex Logarithm
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's discuss where we might use the complex logarithm in real-life applications. Can someone suggest an area?

What about fluid dynamics or potential functions?

Absolutely! The complex logarithm helps analyze fluid flow by simplifying complex potential functions. Can anyone think of an equation it might help solve?

Maybe equations that involve exponential terms?

Yes, precisely. And it also assists in integration within the complex plane. Understanding these applications highlights the importance of master concepts like the complex logarithm!

So it sounds like this would be important for engineers?

Exactly! Structural engineers, fluid dynamics experts, and anyone working with oscillatory systems will find this concept valuable in their work!

To wrap up today, the complex logarithm is essential in various engineering applications, showcasing how integral math is to real-world problems.
Understanding the Multi-Valued Nature
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s take a deeper dive into the multi-valued aspect of the complex logarithm. Why is this a crucial point?

Because it means we can get many values for z, depending on n?

Spot on! Each integer n gives us a different angle rotation around the complex plane. How might this affect calculations?

It could lead to confusion if we don’t specify which value we are using!

Exactly! This is why we rely on using the principal value to avoid ambiguity, which also helps in applications like numerical methods or simulations.

So, is there a specific way we denote the principal value?

Good question! We denote it as Log(z) = ln(r) + iΘ, with Θ constrained to (-π, π]. Remember this notation for clarity!

To summarize our discussion, the multi-valued nature of the logarithm is highly significant in applications, demanding the use of a principal value for precise calculations.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The complex logarithm is defined as the inverse of the complex exponential, allowing us to express a complex number in terms of its magnitude and angle. This logarithm, however, is multi-valued due to periodicity in the complex plane, leading to significant applications in solving equations, integration, and fluid dynamics.
Detailed
Logarithm of a Complex Number
The complex logarithm is defined as the inverse of the complex exponential function. If a complex number is expressed in polar form as $$ z = re^{i heta} $$, then the complex log is given by:
$$ ln(z) = ext{ln}(r) + i heta $$.
Here, both r and θ represent important properties of the complex number, where r is the modulus and θ is the argument. However, due to the periodic nature of the complex exponential function (where $$ e^{i heta} = e^{i( heta + 2 ext{π}n)} $$ for all integers n), the logarithm becomes a multi-valued function. Thus, the complex logarithm can take on infinitely many values, expressed as:
$$ ln(z) = ln(r) + i( heta + 2 ext{π}n) $$.
The principal value of the logarithm, often used to simplify calculations, is given as:
$$ Log(z) = ln(r) + iΘ $$, where Θ is constrained to the interval (-π, π].
This complex logarithm is crucial in various applications such as solving equations with exponential terms, integrating functions in the complex plane, and analyzing fluid dynamics, particularly in the study of potential functions.
Youtube Videos
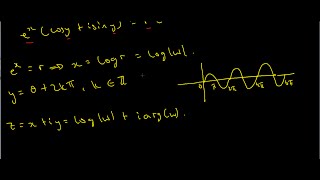

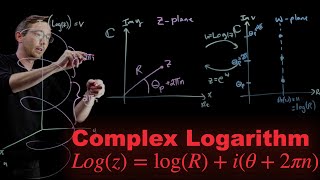
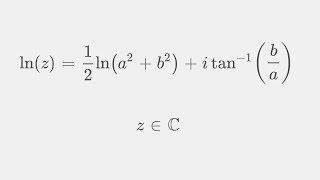






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of the Complex Logarithm
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The complex logarithm is defined as the inverse of the complex exponential:
If z = re^(iθ), then:
lnz = lnr + iθ
Detailed Explanation
In this chunk, we learn about the complex logarithm. The logarithm helps us find the original value (the input) when we know its exponential form (the output). The notation 'z = re^(iθ)' represents a complex number, where 'r' stands for the magnitude (or modulus) and 'θ' for the angle (or argument) on the complex plane. Therefore, the logarithm of 'z' can be expressed as the natural logarithm of the magnitude 'r' plus 'iθ', where 'i' is the imaginary unit. This means the logarithm blends a real number (lnr) and a complex component (iθ).
Examples & Analogies
Imagine you have a factory producing two types of products, and the total output can be represented as a ‘complex product’ combining the quantities of each. To find back to how much of each product you started with (the logarithm), you need to recognize the total (exponential value) and how those products relate to one another (magnitude and angle).
Multi-valued Nature of the Logarithm
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
But here, θ is multi-valued, since: eiθ = ei(θ+2πn), n ∈ Z
Detailed Explanation
The logarithm has a unique characteristic: it is multi-valued for complex numbers. This is because the angle 'θ' can repeat every 2π radians in the complex exponential function. For example, an angle of π can also be represented as π + 2π, π + 4π, and so forth, leading to multiple possible values for the logarithm. 'n' is an integer that represents how many full circles (2π) we add to the angle, reflecting that there are infinitely many equivalent angles for any given complex number.
Examples & Analogies
Think of whirlpools where water swirls clockwise or counterclockwise indefinitely. No matter how many times you loop around, you will end up back in the same location. Similarly, the multiple rotations in the logarithm indicate that you can keep adding 360 degrees (or 2π radians) to the angle without changing the actual position of the point on the complex plane.
Principal Value of Logarithm
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So the logarithm is a multi-valued function:
lnz = lnr + i(θ + 2πn)
Principal Value:
Log z = lnr + iΘ, where Θ ∈ (−π, π]
Detailed Explanation
To handle the multi-valued nature of the logarithm, we define a principal value. This means we select a specific value for 'θ' (denoted as 'Θ') that lies within the interval (−π, π]. By doing so, we ensure that whenever we calculate the logarithm of a complex number, we find one 'standard' value rather than the infinitely many options available. This makes computations more manageable and consistent, especially in engineering applications.
Examples & Analogies
Imagine a cookie jar with an infinite number of cookies. Each cookie shape represents one of the many values of the logarithm. To avoid confusion, we decide to organize the cookies by selecting only the round ones to represent one specific type of cookie (the principal value). This way, whenever we need to refer to cookies, we know we're talking about that specific shape.
Applications of Complex Logarithm
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Applications:
• Used in solving equations involving exponential terms.
• Appears in integration in the complex plane.
• Important in fluid flow problems involving potential functions.
Detailed Explanation
The complex logarithm has practical applications in various fields, especially in engineering and physics. It's vital in solving equations that involve exponential functions, which frequently occur in various systems. Additionally, during the integration of functions in the complex plane, the logarithm is often employed to simplify calculations. Moreover, in fluid dynamics, the logarithm assists in analyzing potential functions that describe fluid flow patterns.
Examples & Analogies
Think about navigation in a coastline where you need to plot your journey. Each change in direction might be likened to a logarithmic calculation, determining your current location (complex numbers) based on your past positions (exponential functions). Understanding the logarithm helps ensure that each segment of your route is accurately gauged under the complex conditions of tides and currents!
Key Concepts
-
Complex Logarithm: The inverse of the complex exponential function with a multi-valued nature.
-
Principal Value: The main value selected from multiple outputs of logarithmic functions.
-
Polar Form: An expression format for complex numbers utilizing modulus and argument.
-
Multi-valued Function: A characteristic of some functions, where multiple outputs can exist for a single input.
Examples & Applications
For a complex number z = 2e^(iπ/3), the logarithm can be calculated as ln(z) = ln(2) + i(π/3 + 2πn), n ∈ Z.
To find the principal value of ln(z) for z = -1, we express it as ln(1) + i(π + 2πn) and take n = 0, yielding: Log(-1) = iπ.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To find the log of what you see, remember to consider periodicity!
Stories
Imagine a spiral staircase, where each step represents a different value of n for the complex logarithm—where choosing the right step ensures a smooth journey through mathematics!
Memory Tools
Principle for Logs: 'r' from Radial, 'θ' from Tangential, gives us the base to evaluate!
Acronyms
LOG
logarithm's Outputs are multi-valued
Generalize with periodicity!
Flash Cards
Glossary
- Complex Logarithm
The complex logarithm is the inverse of the complex exponential function, expressed in terms of modulus and argument, and it is a multi-valued function.
- Polar Form
A way to express complex numbers using modulus and argument, typically written as z = re^(iθ).
- Multivalued Function
A function that can yield multiple outputs for a given input, such as the complex logarithm due to periodicity.
- Principal Value
The value chosen from the multi-valued outputs of a function, such as Log(z) = ln(r) + iΘ, where Θ is restricted to (-π, π].
- Exponential Terms
Mathematical expressions involving the base of natural logarithm raised to a power, commonly used in equations dealt with logarithms.
Reference links
Supplementary resources to enhance your learning experience.
