Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Addition Rule
Unlock Audio Lesson
Today, we're starting with the addition rule of complex exponentials. Can anyone tell me what happens when we add two complex numbers in the exponential form?
I think the result combines them somehow?
Correct! The addition rule states that $$ e^{z_1 + z_2} = e^{z_1} imes e^{z_2} $$. This means that adding the exponents corresponds to multiplying their exponentials.
So if I had $$ z_1 = 1 + 2i $$ and $$ z_2 = 2 + 3i $$, I would add the real parts and the imaginary parts separately?
Exactly! You would get $$ e^{(1+2i) + (2+3i)} = e^{3 + 5i} = e^3 e^{5i} $$. Great job!
Can we use this property in engineering applications?
Absolutely! It's widely used in signal analysis and control systems, where combining waveforms is essential.
In summary, the addition rule allows us to multiply exponentials when adding their exponents. This property is fundamental in many mathematical applications.
Modulus
Unlock Audio Lesson
Next, let's explore the modulus of the complex exponential function. Can someone explain what the modulus of a complex number is?
It's the distance from the origin in the complex plane, right?
Exactly! For our complex exponential, the modulus is given by $$ |e^{z}| = |e^{x + iy}| = e^x $$. Here, the imaginary part does not affect the modulus.
So, if $$ z = 3 + 4i $$, the modulus would be $$ e^3 $$?
Correct! Remember, the imaginary part contributes to the angle in the complex plane, not the magnitude. This property shows how increasing the real part results in exponential growth.
To summarize, the modulus depends solely on the real component of the complex exponential, illustrating growth or decay in various applications.
Periodicity and Derivatives
Unlock Audio Lesson
Now, let's talk about the periodic nature of complex exponentials. Who can tell me what we mean by periodicity?
It means the function repeats itself after a certain interval.
Great! For complex exponentials, we have $$ e^{z + 2πi} = e^z $$, reflecting periodic behavior due to the nature of sine and cosine.
Why does this happen?
It happens because both sine and cosine functions are periodic with periods of $$ 2π $$, mathematically establishing that. Now, regarding derivatives, what do we know?
The derivative of an exponential function is the function itself!
Exactly! The derivative $$ \frac{d}{dz} e^z = e^z $$ holds for complex exponentials. This makes them unique and powerful, especially when solving differential equations.
In closing, periodicity emphasizes the repeating nature of complex exponentials, while differentiation shows us their inherent stability across changes in the input.
Multiplicative Inverse
Unlock Audio Lesson
Lastly, let’s look at the multiplicative inverse of complex exponentials. What does it mean to have an inverse?
It’s what you multiply by to get one!
Right! For complex exponentials, the inverse is given by $$ e^{-z} = \frac{1}{e^z} $$, where we take the negative exponent.
So, $$ e^{-3+4i} $$ would be $$ \frac{1}{e^{3-4i}} $$?
Exactly! This property is useful in many calculations, especially when simplifying expressions involving complex numbers.
Does this apply in any practical problem-solving situations?
Indeed! It’s essential in electrical engineering and systems involving feedback loops.
To summarize, the multiplicative inverse of a complex exponential helps in solving equations and integrating complex functions effectively.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section outlines key properties of the complex exponential function, emphasizing its significance in mathematical applications such as engineering and physics. It details rules related to addition, modulus, periodicity, derivative functionalities, and the concept of multiplicative inverse.
Detailed
Properties of the Complex Exponential Function
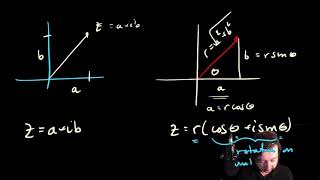
In this section, we explore crucial properties of the complex exponential function, which is defined as:
$$ e^z = e^{x+iy} = e^x ( ext{cos}(y) + i ext{sin}(y)) $$.
Key Properties:
- Addition Rule:
- Formula: $$ e^{z_1 + z_2} = e^{z_1} imes e^{z_2} $$
- This property demonstrates how the exponential function behaves under addition.
- Modulus:
- Formula: $$ |e^z| = |e^{x+iy}| = |e^x( ext{cos}(y) + i ext{sin}(y))| = e^x $$
- The modulus of the complex exponential only depends on the real part, indicating growth or decay.
- Periodicity:
- Property: $$ e^{z + 2 ext{π}i} = e^z $$
- This reflects the periodic nature of the function due to the cyclic nature of cosine and sine.
- Derivative:
- Formula: $$ rac{d}{dz} e^z = e^z $$
- The derivative of the complex exponential function is unique as it remains unchanged.
- Multiplicative Inverse:
- Formula: $$ e^{-z} = rac{1}{e^z} $$
- This property helps in calculating inverses within complex numbers.
Significance:
These properties form the backbone for dealing with oscillatory phenomena found in engineering and physics, particularly in analyzing waveforms, electrical circuits, and dynamic systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Addition Rule
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Addition Rule:
ez1+z2 = ez1 · ez2
Detailed Explanation
The Addition Rule states that when you add two complex numbers in exponential form, you can convert that addition into a multiplication of their separate exponential forms. This means if you have two complex numbers, z1 and z2, you can find the exponential of their sum by multiplying the exponentials of the individual numbers. This property is similar to how we can combine exponents in the base case of real numbers, where a^m * a^n = a^(m+n).
Examples & Analogies
Imagine you’re mixing two different color paints. Each color represents a complex number in exponential form. When you mix them, rather than just adding them like basic colors, you multiply their potential by weaving their unique shades (or exponential functions), resulting in a new hue, much like how the exponentials combine to form a new value.
Modulus
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Modulus:
|ez|=|ex+iy|=|ex(cosy+isiny)|=ex
Detailed Explanation
The modulus of a complex exponential function indicates its 'size' or distance from the origin in the complex plane. This property shows that the modulus only depends on the real part of the complex number. Specifically, for any complex number z = x + iy, ez transforms it into a magnitude based on ex, where e is raised to the power of the real part. This suggests that the oscillatory nature introduced by the imaginary part does not affect the distance from the origin.
Examples & Analogies
Think of a lighthouse where the light travels in circles. The brightness (modulus) of the light depends on the power supply (real part, e^x), regardless of how fast the light rotates (the imaginary part, e^(iy)). As long as the power remains constant, the brightness stays the same even if the light source rotates.
Periodicity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Periodicity:
ez+2πi = ez (since cos(y+2π)=cosy,sin(y+2π)=siny)
Detailed Explanation
The property of periodicity indicates that the complex exponential function is periodic with respect to its imaginary component. When you add 2πi (a full rotation in the complex plane), the function returns to its initial value. This is analogous to how sine and cosine functions repeat their values every 2π radians, reflecting a cyclic behavior.
Examples & Analogies
Think of a Ferris wheel that completes a full turn (2π) to return to the top position. Each time it goes around, the passengers experience the same view from the top. Similarly, after every full rotation represented by 2π in complex exponentials, the output returns to the same position, illustrating periodicity.
Derivative
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Derivative:
dez = ez
dz
Detailed Explanation
The derivative of the complex exponential function with respect to z shows that the function maintains its form. It indicates that the rate of change of ez does not depend on the actual value of z; rather, it remains proportional to itself. This property is significant in various applications, including signal processing and differential equations, because it simplifies calculations involving rates of change.
Examples & Analogies
Consider how a sound wave propagates. The speed at which the sound travels (its derivative) remains constant regardless of the frequency—it simply scales the sound’s amplitude. Similarly, the derivative of the complex exponential shows that its growth or decay (as represented by e^z) is consistently predictable, making it easier to analyze and model.
Multiplicative Inverse
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Multiplicative Inverse:
1
e−z =
ez
Detailed Explanation
The concept of the multiplicative inverse in the context of complex exponentials indicates that to find the inverse of an exponential function, you simply take the exponential of the negative of the complex number. This tells us that every complex exponential function has a reciprocal that corresponds to an opposing rotation in the complex plane, maintaining the relationships between different exponential values.
Examples & Analogies
Think about a swimmer in a pool: when they swim in one direction (e^z), they have a certain speed. If they want to effectively reverse that direction (the inverse), they have to swim at the same speed but in the opposite direction (e^(-z)). This inverse relationship illustrates how complex exponentials can mirror each other when one is negative.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Addition Rule: Describes how to add complex exponentials through multiplication.
-
Modulus: The magnitude of the exponential function which depends only on the real part.
-
Periodicity: Indicates the repeating nature of the complex exponential function.
-
Derivative: Shows that the derivative is identical to the function itself, making it unique among other function types.
-
Multiplicative Inverse: Represents how to find the inverse of a complex exponential to facilitate complex calculations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using the addition rule, if z1 = 1 + 2i and z2 = 2 + 3i, we find e^(z1 + z2) = e^3 * e^(5i).
-
Calculating modulus, for z = 3 + 4i, |e^z| = e^3, demonstrating how the magnitude is derived solely from the real part.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When dealing with sums of exp's, remember this fact: Multiply them together, and you'll stay on track.
📖 Fascinating Stories
-
Imagine two friends, Alpha and Beta, who each hold an exponential secret. By combining their secrets, they create a new reality, emphasizing the power of addition.
🧠 Other Memory Gems
-
To remember properties of the complex exponential, think 'AMDP': Addition, Modulus, Derivative, Periodicity.
🎯 Super Acronyms
Use the phrase 'M-PAD' to recall Modulus, Periodicity, Addition, Derivative.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Complex Exponential Function
Definition:
A function of the form $$ e^{x + iy} $$ that combines real and imaginary exponent values.
-
Term: Addition Rule
Definition:
A property that states that the exponential of a sum of two complex numbers equals the product of their exponentials.
-
Term: Modulus
Definition:
The magnitude or length of a complex number, which can determine growth or decay in exponential functions.
-
Term: Periodicity
Definition:
The quality of a function to repeat its values at regular intervals.
-
Term: Derivative
Definition:
A measure of how a function changes as its input changes; for complex exponentials, it equals the function itself.
-
Term: Multiplicative Inverse
Definition:
A number that, when multiplied by a given number, results in one.