Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Damped Harmonic Motion
Unlock Audio Lesson
Today, we'll discuss damped harmonic motion, a critical concept in mechanical and civil engineering. Can anyone tell me what damping refers to in this context?
Isn't it what causes the oscillations to gradually decrease in amplitude?
Exactly! Damping is the effect that reduces the amplitude of oscillations over time. It can be modeled using the equation y(t) = e^(-αt)(Acos(ωt) + Bsin(ωt)). The term e^(-αt) represents the damping factor.
What do A and B represent in that equation?
Great question! A and B are constants that depend on the initial conditions of the system, and they determine the specific shape of the oscillation. This concept is vital for modeling real-world systems.
How does this relate to civil engineering?
Damped oscillations can be observed in structures under dynamic loads, such as seismic vibrations in buildings and suspension bridges. Understanding these principles helps engineers design safer structures.
In summary, damped harmonic motion describes how oscillations decrease in amplitude over time due to damping, which is crucial for engineering applications.
Role of Complex Exponentials in Damped Motion
Unlock Audio Lesson
Now, let's dive deeper into how complex exponentials fit into the equation of damped harmonic motion. Who can represent y(t) in terms of a complex exponential?
Is it y(t) = Re(Ce^((-α + iω)t))?
Excellent! This representation shows that we can express damped motion using complex exponentials. The term 'Re' denotes the real part of the complex function, which gives us the actual physical displacement.
Why use complex exponentials instead of just sine and cosine functions?
Complex exponentials allow us to simplify calculations, particularly when working with differential equations. They make it easier to manipulate oscillatory functions and identify relationships between parameters.
So, using complex numbers helps in solving differential equations more efficiently in engineering?
Absolutely right! Complex exponentials streamline the process of finding solutions for systems modeled by second-order differential equations.
To summarize, representing damped harmonic motion using complex exponentials allows for simplification in calculations and enhances the clarity of oscillatory behavior in engineering contexts.
Applications of Damped Harmonic Motion
Unlock Audio Lesson
Let’s talk about some real-world applications of damped harmonic motion. Can anyone think of situations where this concept is vital?
How about in designing buildings to withstand earthquakes?
Exactly! In seismic design, we need to account for the damped response of structures during and after seismic events to ensure they can withstand vibrations.
Do suspension bridges also use this concept?
Yes, they do! Engineers have to consider the damped oscillation of bridge structures when analyzing their response to dynamic loads, particularly from traffic and wind.
Can it be applied to other structures, too?
Absolutely. This concept applies to any structure subject to dynamic loading, helping engineers design safe and resilient systems.
In conclusion, understanding damped harmonic motion helps in the effective design and analysis of structures, especially those exposed to dynamic forces like earthquakes and winds.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Damped harmonic motion can be represented through the equation y(t) = e^(-αt)(Acos(ωt) + Bsin(ωt)), demonstrating how complex exponentials emerge in the analysis of oscillatory motion, seismic vibrations, and structural response to dynamic loads.
Detailed
In this section, we explore the concept of damped harmonic motion, characterized by the equation y(t) = e^(-αt)(Acos(ωt) + Bsin(ωt)), where α represents damping, ω the angular frequency, and C a complex constant. This formulation exemplifies how complex exponentials arise from second-order differential equations encountered in civil engineering, particularly for modeling scenarios like seismic vibrations in buildings and structural responses in suspension bridges. Understanding these relationships is essential for engineers dealing with dynamic loads and vibrations in structures.
Youtube Videos
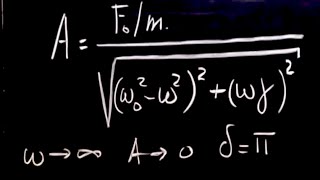
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Modeling Damped Oscillation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A general damped oscillation can be modeled using:
y(t) = e^{-αt}(Acos(ωt) + Bsin(ωt)) = Re Ce^{(−α+iω)t}
Detailed Explanation
This equation represents a damped harmonic motion, which describes systems that lose energy over time, typically due to friction or other forms of resistance. The term e^{-αt} signifies the damping factor where α controls how quickly the oscillations decay over time. The components Acos(ωt) and Bsin(ωt) represent the oscillatory nature of the motion, where ω is the angular frequency of the oscillation. This formulation can also be expressed in terms of a complex exponential, showing how complex numbers are used to simplify and represent these types of motions.
Examples & Analogies
Imagine a swinging pendulum that starts off swinging high but gradually slows down and comes to a stop due to air resistance and friction at the pivot point. Initially, the pendulum moves in a regular arc, but over time, it loses energy, resulting in reduced swing amplitude. The mathematical equation captures this gradual decrease in swing height and frequency, similar to how our real-world experiences of damping work.
Components of Damped Harmonic Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Where:
• α controls damping (decay),
• ω is the angular frequency,
• C is a complex constant.
Detailed Explanation
In the context of damped harmonic motion, α, ω, and C each have specific roles. The parameter α indicates how quickly the amplitude of the oscillation decreases over time due to damping. A larger α value means quicker decay. The angular frequency ω determines how rapidly the system oscillates; it defines how many cycles are completed in a given time frame. Lastly, C, a complex constant arises from combining contributions from both sine and cosine components in the harmonic motion, facilitating easier manipulation of the overall function in mathematical terms.
Examples & Analogies
Consider a car tire that has a slow leak. The slow leak represents the damping, where α is strong if the leak is rapid (quickly losing air) and weak if it leaks slowly. The car's movements (oscillation) depend on how fast the tire can rotate (ω), while C could be thought of as how well the tire maintains its performance even as it bounces (reconstructing the interaction between complex components). These parameters together help predict the tire's behavior over time.
Applications in Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This shows how complex exponentials naturally arise in second-order differential equations related to:
• Seismic vibrations in buildings,
• Suspension bridges,
• Structural response to dynamic loads.
Detailed Explanation
The equation illustrating damped harmonic motion is particularly relevant in engineering applications where structures must react to dynamic forces, such as earthquakes or wind loads. The use of complex exponentials in these contexts allows engineers to analyze and predict the behavior of structures under such conditions effectively. The damping factor helps determine how much the oscillations will decrease over time, ensuring that buildings can withstand external forces without collapsing.
Examples & Analogies
Think of a skyscraper during an earthquake. The designers use complex exponential functions to model how the building sways and absorbs the seismic energy, helping to ensure its stability. If there's too much sway or the damping (energy absorption) isn't sufficient, the building could sustain damage. Just as a dancer adjusts their movements to maintain balance while twirling, engineers must predict and control oscillations in structures to keep them safe during unexpected forces.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Damped Harmonic Motion: Motion where amplitude decreases due to damping.
-
Complex Exponentials: Functions that simplify the representation of oscillatory motions.
-
Damping Factor: The rate at which damped oscillations decay.
-
Angular Frequency: The speed of oscillations in radians per second.
-
Modeling with Complex Numbers: Efficient representation of solutions to differential equations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The motion of a pendulum that loses energy due to air resistance is a real-world example of damped harmonic motion.
-
In civil engineering, the behavior of a bridge under varying loads can be modeled with damped harmonic motion to ensure structural integrity.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the damper's sway, the amplitude's way, diminishes over time, like a soft lullaby.
📖 Fascinating Stories
-
Imagine a swing in the park; as the kids stop pushing, it slows down gradually. This is like damped motion where energy fades over time.
🧠 Other Memory Gems
-
DAMP: D = Damping factor, A = Amplitude reduction, M = Motion decay, P = Periodic behavior.
🎯 Super Acronyms
DAMP
- (Damping
- Amplitude
- Motion
- Physics). Use it to remember the key aspects of damped harmonic motion.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Damped Harmonic Motion
Definition:
Oscillatory motion characterized by a decrease in amplitude over time due to energy loss.
-
Term: Complex Exponential
Definition:
A mathematical expression of the form e^(α + iω)t, where α represents decay and ω represents oscillation.
-
Term: Damping Factor (α)
Definition:
A constant that controls the rate at which amplitude decreases in a damped oscillation.
-
Term: Angular Frequency (ω)
Definition:
The rate of oscillation, typically measured in radians per second.
-
Term: Complex Constant (C)
Definition:
A coefficient that includes both real and imaginary parts in a complex function.