Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding e^ix
Unlock Audio Lesson
Today, we're going to explore the function e^ix. Does anyone know how this function is expressed using Euler's formula?
Isn't it something like e^ix = cos(x) + i sin(x)?
Exactly! That's correct. This identity is called Euler's formula, and it shows how the complex exponential can be represented as a combination of cosine and sine functions. Can anyone tell me what each part represents?
The real part is cos(x) and the imaginary part is sin(x).
Right! Remember, the real part corresponds to the cosine function, which relates to horizontal movement, while the imaginary part corresponds to the sine function, representing vertical movement. This gives us a geometric representation in the complex plane.
So, e^ix traces a unit circle, right?
Yes, it does! That's a great observation. As x increases, the point represented by e^ix moves around the unit circle, which is critical in oscillatory systems.
Application of Real and Imaginary Parts
Unlock Audio Lesson
Now that we understand the decomposition of e^ix, let's discuss its applications, especially in Fourier analysis. Can anyone explain what Fourier analysis is?
Isn't that where we break down signals into sine and cosine components?
Exactly! By expressing signals as a sum of cosines and sines, analysts can understand their frequency components. How does knowing the real and imaginary parts of e^ix help in this analysis?
It allows us to transform complex signals into simpler trigonometric forms, making calculations easier.
Well said! When we identify components as cosines and sines, we can work with trigonometric identities to solve various problems more effectively.
Importance in Engineering Fields
Unlock Audio Lesson
Let's talk about the importance of e^ix in engineering. Why do you think the real and imaginary parts are vital in fields such as civil engineering?
Because we encounter a lot of oscillatory motions, like vibrations in structures, right?
Absolutely! Engineers analyze these vibrations using sine and cosine functions derived from e^ix. They can assess system stability and performance under oscillatory loads. Can anyone provide an example of where this might be applied?
In analyzing the vibrations of a bridge under traffic loads!
Perfect example! This method allows engineers to design safer and more efficient structures. It reinforces the unifying role that complex exponentials play in both mathematics and engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses how the complex exponential function e^ix can be expressed as the sum of its real part, cos(x), and its imaginary part, sin(x). This decomposition is crucial for applications such as Fourier analysis, where functions can be expressed in terms of sine and cosine functions, allowing for easier manipulation and analysis.
Detailed
Detailed Overview of Real and Imaginary Parts of e^ix
In this section, we delve into the function e^ix, which can be expressed using Euler's formula as:
$$ e^{ix} = cos(x) + i sin(x) $$
The real part of this expression is given by the cosine function, while the imaginary part is represented by the sine function:
- Real Part: $$ Re(e^{ix}) = cos(x) $$
- Imaginary Part: $$ Im(e^{ix}) = sin(x) $$
This decomposition is not merely theoretical; it has practical applications in various fields, particularly in Fourier analysis. In this context, signals can be modeled as sums of sine and cosine components, facilitating easier handling and analysis. Understanding this breakdown enables engineers and scientists to leverage the properties of trigonometric functions within the framework of complex analysis, especially when analyzing oscillatory phenomena and waveforms.
Youtube Videos
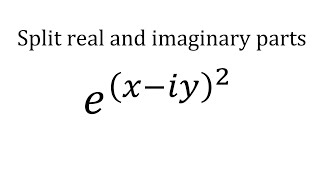
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding e^ix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The function eix can be dissected into its real and imaginary components, which are the cosine and sine functions, respectively:
eix = cosx + isin x
Detailed Explanation
The function e raised to an imaginary number (e^ix) can be split into two parts: the real part (cos(x)) and the imaginary part (sin(x)). This is effectively a way to represent the complex exponential function in terms of familiar trigonometric functions, where 'x' corresponds to an angle measured in radians.
Examples & Analogies
Think of e^ix as a way to describe the position of a point on a rotating wheel. As the wheel turns, the x-coordinate corresponds to its real part (cos(x)), while the height of the wheel corresponds to its imaginary part (sin(x)). This representation helps visualize the wheel's movement in a more mathematical way.
Real Part of e^ix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So:
• Real Part: Re(eix) = cosx
Detailed Explanation
The real part of e^ix is calculated as cos(x). This function describes how far left or right the point is positioned on the unit circle, which represents all the possible values of e^ix as it rotates around the circle. Thus, as 'x' changes, the cosine value varies, tracing the horizontal distance from the center of the circle.
Examples & Analogies
Imagine you're observing waves in the ocean. As the waves rise and fall (the imaginary component), at any given moment, you can only see how high the water is (the real component). The higher the wave, the bigger the cosine value, showing how far the wave is pushing outward from the calm water surface.
Imaginary Part of e^ix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Imaginary Part: Im(eix) = sinx
Detailed Explanation
The imaginary part of e^ix is represented by sin(x). This function accounts for the vertical position of the point on the unit circle, showing how high or low the point reaches as the angle 'x' changes. The sine function varies between -1 and 1, illustrating the up and down movement of the point on the circle's edge.
Examples & Analogies
Consider a pendulum swinging back and forth. At its highest point, it stops, and while swinging through its lowest point, it moves fastest. The imaginary part illustrates the vertical component of this motion at any point in time, similar to measuring the height of the pendulum above the ground.
Applications in Fourier Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This breakdown is not just a theoretical formality—it has applications in Fourier analysis, where signals are decomposed into sine and cosine (or exponential) components.
Detailed Explanation
The representation of complex exponentials in terms of sine and cosine has practical applications in Fourier analysis. Here, any periodic signal can be expressed as a sum of sine and cosine functions, making it easier to analyze and process signals in a variety of fields, including engineering and physics.
Examples & Analogies
Imagine a musician playing a complex chord on a piano. By understanding the individual notes (sine and cosine components), one can analyze the chord's structure. Similarly, in signals, breaking them into simpler sine and cosine components helps engineers design better communication systems by understanding how different frequencies interact.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Complex Exponential: A function where complex numbers are expressed using exponential terms.
-
Real Part: The cosine component of a complex function.
-
Imaginary Part: The sine component of a complex function.
-
Fourier Analysis: Technique for breaking down signals into sine and cosine components.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For e^(iπ), using Euler's formula, we find e^(iπ) = cos(π) + i*sin(π) = -1.
-
In alternating current (AC) analysis, using e^(iωt) allows the simplification of current and voltage equations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find e to the ix, just use cos and sin, it's a delightful mix!
📖 Fascinating Stories
-
Imagine a traveler on a unit circle, dancing around — cos(x) shows the distance along the x-axis while sin(x) takes them up the y-axis.
🧠 Other Memory Gems
-
For e^ix, remember 'C's for cos, and 'S's for sin. C before S in the circle!
🎯 Super Acronyms
COSINE
- C: is for the Cosine part and S is for Sine
- to remember the real and imaginary components.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Euler's Formula
Definition:
A formula stating e^(ix) = cos(x) + i sin(x), which expresses complex exponentials in terms of trigonometric functions.
-
Term: Complex Exponential Function
Definition:
The function of a complex number that can be expressed in terms of exponential, sine, and cosine functions.
-
Term: Fourier Analysis
Definition:
A mathematical method for decomposing signals into sine and cosine components for easier analysis.
-
Term: Real Part
Definition:
The cosine component of a complex exponential function.
-
Term: Imaginary Part
Definition:
The sine component of a complex exponential function.