Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Euler's Formula
Unlock Audio Lesson
Today, we're diving into Euler's Formula, which states e^(ix) = cos(x) + i*sin(x). Let's start by breaking this down. What do you think the importance of this formula is?
I think it's important for understanding complex numbers, but how does it relate to real numbers?
Great question! This formula is actually a bridge between complex exponential functions and real trigonometric functions. It demonstrates how a complex number can be represented in terms of sine and cosine.
So, it’s like visualizing a point on the unit circle in the complex plane?
Exactly! When we plot e^(ix) on the complex plane, it describes a rotation around the origin, which corresponds to the angle x.
How do we use this in engineering contexts?
Euler's Formula is fundamental in understanding oscillatory phenomena like vibrations and waves in structures. We'll see more applications as we progress.
Applications of Euler's Formula
Unlock Audio Lesson
Now, let's focus on the applications. Can anyone think of an instance where Euler's Formula comes into play?
Maybe in alternating currents and how we analyze them?
Precisely! When we analyze electrical circuits, we use Euler’s Formula to express voltage and current in complex form. It simplifies our calculations significantly.
What about in solving differential equations?
Excellent point! Many differential equations lead to solutions involving complex exponentials thanks to this formula. In vibrations and wave analysis, it becomes crucial.
Can you summarize the key ideas from this session?
Sure! Euler’s Formula connects complex exponentials to trigonometric functions and has vast applications in engineering, particularly in oscillatory motion and electrical signals.
Euler’s Formula’s Significance
Unlock Audio Lesson
To wrap up, why do you think Euler's Formula is described as the 'crown jewel' of mathematics?
Maybe because it connects so many areas of math—like calculus, trigonometry, and complex analysis!
Exactly! It beautifully unifies these domains and is central to many fundamental concepts, such as the Fourier transform.
And it also illustrates how imaginary numbers can be understood in a real context!
Spot on! Recognizing the role of imaginary numbers through Euler’s Formula opens up applications in engineering and physics.
So, are we ready to see some practical problems involving Euler's Formula?
Absolutely! Let’s transition into exercises that will help solidify our understanding.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explores Euler's Formula, e^(ix) = cos(x) + i*sin(x), highlighting its significance in connecting complex exponential functions with trigonometric identities. It discusses the interpretation of this formula on the unit circle and its foundational role in complex analysis and engineering applications.
Detailed
Detailed Summary of Euler’s Formula
Euler’s Formula is given by:
e^(ix) = cos(x) + i*sin(x)
Where:
- i is the imaginary unit with the property i^2 = -1.
- x represents a real number (usually the angle in radians).
Interpretation
Euler's Formula articulates how a complex exponential can be decomposed into real trigonometric functions.
Geometrically, it represents the unit circle on the complex plane, where any point can be expressed as a combination of its cosine (the x-coordinate) and sine (the y-coordinate) components. This representation is critical in engineering applications, particularly in analyzing oscillatory and wave-like phenomena such as vibrations in structures and alternating currents.
Key Points Covered:
- Complex Exponential Function: The definition of the exponential of a complex number and its significance in both engineering and mathematics, showing how it maps spirals in the complex plane.
- Applications: The foundational nature of Euler’s Formula in solving differential equations, transforming trigonometric identities, and facilitating the understanding of complex numbers and their powers.
Understanding Euler’s Formula is crucial for students in fields related to engineering and applied mathematics, as it provides insight into the nature of oscillations and functions that can be represented in both exponential and trigonometric forms.
Youtube Videos
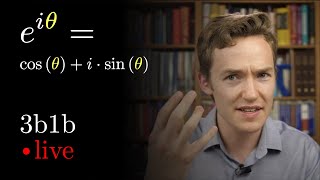
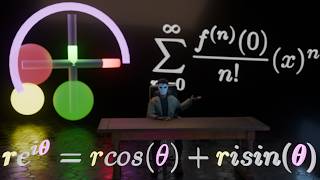
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Euler's Formula
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Euler's formula forms the cornerstone of the complex exponential function:
e^{ix} = ext{cos} x + i ext{sin} x
Detailed Explanation
Euler's formula establishes a deep relationship between complex exponential functions and trigonometric functions. In this equation, e is the base of natural logarithms, i represents the imaginary unit defined as √(-1), and x is a real number that represents an angle in radians. The equation states that for any real number x, the complex exponential function can be expressed as the sum of the cosine and sine functions multiplied by i. This relationship highlights how complex numbers can be visualized in terms of rotations in a plane.
Examples & Analogies
Think of it like a musical instrument where the notes (cosine and sine) combine to create a harmonious tune (the complex exponential). Just like how different musical notes come together to create a melody, the cosine and sine functions combine to give rise to the complex exponential function.
Understanding the Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
where:
• i is the imaginary unit, i² = −1,
• x is a real number (angle in radians).
Detailed Explanation
In the equation, the term i is not just any number; it represents the imaginary unit. The definition i^2 = −1 means that when you square i, you get a negative result, which does not exist in the world of real numbers. The variable x is a real number that can be used to represent angles, particularly useful when discussing rotation and oscillation in engineering contexts. The angle must be in radians for the trigonometric functions to accurately represent the behavior of the system being modeled.
Examples & Analogies
Consider x as the rotation of a wheel. When the wheel turns by x radians, the imaginary unit i helps us track its position in a direction that we cannot see directly (like a shadow of the wheel on a 2D surface).
Geometric Interpretation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Euler's formula expresses a complex exponential as a combination of real trigonometric functions. It geometrically represents a point on the unit circle in the complex plane.
Detailed Explanation
Euler's formula can be visualized in the complex plane, where the x-axis represents the real part and the y-axis represents the imaginary part. The equation e^{ix} describes points that lie on the unit circle, which has a radius of one. As the angle x varies, the coordinates (cos x, sin x) trace out a circle. This geometric interpretation provides insight into the periodic nature of the sine and cosine functions, indicating that as x increases, the point on the unit circle moves around the circle continuously.
Examples & Analogies
Imagine a ferris wheel. As the wheel rotates, it elevates passengers up and down, just as the unit circle traces out the height (real part) and the side-to-side position (imaginary part) of each passenger in a circular motion. The continuous rotation shows how ever-increasing angles map around the circle without limit.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Euler's Formula: e^(ix) = cos(x) + i*sin(x), a fundamental relationship in complex analysis.
-
Complex Exponential Function: A function defined by the exponentiation of a complex number, influencing growth and oscillation characteristics.
-
Unit Circle: A circle of radius one in the complex plane representing all complex numbers of the form e^(ix).
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using Euler's Formula, we can express cos(π) as e^(iπ) = cos(π) + i*sin(π) = -1, demonstrating the formula's utility.
-
In oscillatory motion, the solution of a differential equation can be represented using Euler's Formula, facilitating calculations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Euler's thought, in numbers grand, e^(ix) gives a helping hand. Cos and sin, in harmony sway, on the circle they dance and play.
📖 Fascinating Stories
-
Imagine a complex explorer named Euler, who discovered a magical relationship connecting the lands of exponential and trigonometric kingdoms, where each angle brought harmony and rotation.
🧠 Other Memory Gems
-
Remember 'CSI' for 'cosine, sine, and i' linked by Euler’s formula.
🎯 Super Acronyms
Use the acronym 'EC = CS + IS' to remember Euler's Formula (Euler's Complex = Cosine + i*Sine).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Euler's Formula
Definition:
An equation that establishes a fundamental relationship between complex exponential functions and trigonometric functions. Expressed as e^(ix) = cos(x) + i*sin(x).
-
Term: Complex Number
Definition:
A number that can be expressed in the form a + bi, where a and b are real numbers and i is the imaginary unit.
-
Term: Trigonometric Functions
Definition:
Functions that relate the angles of triangles to the lengths of their sides, including sine, cosine, and tangent.