Polar Form of Complex Numbers and Exponential Notation
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Polar Form
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll be discussing the polar form of complex numbers. You may remember that a complex number can be represented in Cartesian form as z = x + iy. However, there's another way to represent complex numbers that can simplify certain operations. This is known as the polar form. Can anyone tell me what the polar form looks like?

Is it something like z = r(cos θ + i sin θ)?

That’s correct, Student_1! But we can also express this in a more compact notation as z = re^{iθ}. Now, who can remind us what r and θ represent?

r is the modulus of the complex number, which is the distance from the origin in the complex plane, and θ is the argument, or the angle.

Great! Remember, the modulus is calculated as the square root of x squared plus y squared. To recall this, you can think of the acronym 'RADIUS' - for Radius = √(x² + y²).

What’s the significance of using polar form?

Excellent question, Student_3! The polar form simplifies operations such as multiplication and division. Keep that in mind as we progress!
Multiplication and Division in Polar Form
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s dive into some operations. When we multiply two complex numbers in polar form, can anyone tell me what happens to their moduli and arguments?

The moduli get multiplied, and the arguments get added!

Exactly, Student_4! Thus, if we have z_1 = r_1e^{iθ_1} and z_2 = r_2e^{iθ_2}, their product is given by z_1z_2 = r_1r_2e^{i(θ_1 + θ_2)}. Now, how about division?

I think for division, the moduli divide, and we subtract the arguments, so it would be z_1/z_2 = (r_1/r_2)e^{i(θ_1 - θ_2)}.

Correct! Remember, with these operations, we're effectively transforming our complex calculations into simpler and more manageable forms.
Calculating Powers and Roots
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let’s deal with raising a complex number to a power. If we have z = re^{iθ}, how would we calculate z to the nth power?

It would be r^n e^{inθ}!

That's right! This property makes calculations much simpler. Now, let’s talk about finding roots of complex numbers. How can we express the nth root of z?

It would be √[n]{z} = r^{1/n} e^{(i(θ + 2kπ))/n}, for k = 0, 1, ..., n-1.

Well done, Student_3! Thank you all for your contributions today. Remember, mastering these concepts is essential as we dive deeper into the applications of complex numbers!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The polar form of complex numbers expresses a complex number as a product of its modulus and an exponential function involving its argument. This representation simplifies operations like multiplication and division and assists in the computation of powers and roots.
Detailed
Polar Form of Complex Numbers and Exponential Notation
The polar form of a complex number offers a powerful representation that greatly simplifies various operations in both mathematics and engineering. Any non-zero complex number can be expressed in the polar form as:
Polar Form:
$$z = re^{i heta}$$
where:
- r is the modulus (or absolute value) of the complex number, defined as $r = |z|$.
- θ (theta) is the argument (or angle) of the complex number, typically measured in radians.
This form is particularly useful for performing operations involving complex numbers. For example, when multiplying two complex numbers in polar form, the moduli are multiplied and the arguments are added:
Multiplication:
$$z_1z_2 = r_1r_2e^{i( heta_1 + heta_2)}$$
For division, the moduli are divided and the arguments are subtracted:
Division:
$$\frac{z_1}{z_2} = \frac{r_1}{r_2}e^{i( heta_1 - heta_2)}$$
These transformations allow for simpler calculations, especially when raising complex numbers to powers or finding their roots. Understanding the polar form is essential for working with complex numbers in various applications, particularly in fields such as engineering and physics.
Youtube Videos





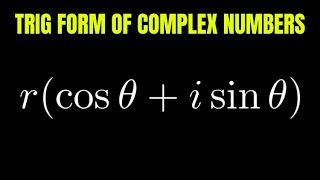




Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Polar Form
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Any non-zero complex number z = r(cosθ + isinθ) can be written as:
z = reiθ
where:
• r = |z| (modulus),
• θ = arg(z) (argument or angle).
Detailed Explanation
The polar form is a way of expressing complex numbers in terms of their magnitude and angle. The modulus 'r' represents the distance of the point from the origin on the complex plane, while 'θ' denotes the angle it makes with the positive real axis. This representation simplifies many calculations, especially when dealing with multiplication and division of complex numbers.
Examples & Analogies
Imagine standing at the center of a circular park. The distance from you to a point on the edge of the park is like 'r', and the direction you're facing relative to the north side of the park is like 'θ'. This way of thinking helps us visualize how to locate points in a two-dimensional space.
Multiplication of Complex Numbers in Polar Form
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This form simplifies multiplication, division, and finding powers and roots of complex numbers.
Multiplication:
z1 z2 = r1 r2 ei(θ1 + θ2)
Detailed Explanation
When multiplying two complex numbers in polar form, you multiply their magnitudes (r1 and r2) together and add their angles (θ1 and θ2). This is effective because it transforms a potentially complex multiplication operation into a simple product of numbers (for magnitudes) and an addition of angles.
Examples & Analogies
Think of combining two efforts in a group project. If one team member is contributing significantly (like a larger r) and the other is adding their own perspective (like an angle), their combined input can be visualized as working from a distance and a direction, creating a new, unified direction for the project.
Division of Complex Numbers in Polar Form
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Division:
z1 / z2 = (r1 / r2) ei(θ1 - θ2)
Detailed Explanation
In division, you divide the magnitudes of the complex numbers and subtract their angles. This makes division straightforward, turning it into a simple ratio of distances and a difference of directions.
Examples & Analogies
Imagine you are sharing a pizza. If one person eats a certain portion (r1) and another eats from a different size pizza (r2), then comparing how much of each pizza was eaten involves dividing portions (like dividing r's) and understanding how their choices differ in direction (like angles).
Key Concepts
-
Polar Form: A representation of complex numbers as z = re^{iθ}.
-
Modulus (r): The magnitude of a complex number, calculated as |z|.
-
Argument (θ): The angle associated with the complex number in the polar coordinate representation.
Examples & Applications
Example: Convert the complex number 3 + 4i into polar form. The modulus r = √(3² + 4²) = 5, and the argument θ = arctan(4/3) = 0.93 radians, so z = 5e^{i0.93}.
Example: Multiply z_1 = 2e^{iπ/4} by z_2 = 3e^{iπ/3}. The product is z_1z_2 = 6e^{i(π/4 + π/3)} = 6e^{i(7π/12)}.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Finding the modulus is a breeze, square and sum with such ease!
Stories
Imagine a traveler in a field, measuring distance and angle, that’s how complex numbers yield.
Memory Tools
Remember 'MATRIX' for Modulus, Angle, TRIGonometric, eXponential; it covers the essentials!
Acronyms
P.O.L.A.R - 'Product of Length And Rotation' for remembering polar form!
Flash Cards
Glossary
- Polar Form
A method of representing complex numbers in the form z = re^{iθ}, where r is the modulus and θ is the argument.
- Modulus
The distance of a complex number from the origin in the complex plane, given by r = |z|.
- Argument
The angle θ that corresponds to the position of a complex number in the polar coordinate system.
Reference links
Supplementary resources to enhance your learning experience.
