Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
The Euler-Bernoulli Beam Equation
Unlock Audio Lesson
Today we will explore the Euler-Bernoulli beam equation, which describes the deflection of beams in civil engineering. Can anyone tell me what variables are involved in this equation?
Is it the load, the length of the beam, and the material properties?
Great start! The main variables are indeed the load q(x), the flexural rigidity EI, and y(x) which represents the beam deflection. We express it as follows: $$\frac{d^4y}{dx^4} = \frac{q(x)}{EI} $$.
What do the terms $$d^4y/dx^4$$ signify?
Excellent question! That term represents the fourth derivative of the deflection concerning x, which correlates with the beam's rigidity and its response to loads. It's crucial for understanding beam behavior.
So, if the load increases, how does that affect the deflection?
Exactly! An increased load will lead to a greater deflection in the beam, which is central to our analysis.
Can we also predict at which point the beam will bend the most?
Yes, typically the deflection is greatest at the free end of the beam, and our analysis will help quantify that. Let’s summarize: The Euler-Bernoulli equation connects load, deflection, and beam properties.
Applying Fourier Cosine Transform
Unlock Audio Lesson
Now, let’s discuss applying the Fourier Cosine Transform. Why do we use this specific transform for beam deflection?
Is it because the beam has fixed ends?
Exactly! The Fourier Cosine Transform is suitable because we analyze the functions defined on a semi-infinite domain. Now, let's see how we apply it. We take the transform of our main equation: $$ F\{\frac{d^4y}{dx^4}\} = s^4Y(s) $$.
So that gives us the transform of the load, correct?
Yes! We equate that to $F\{q(x)\}$, yielding a solution for $Y(s)$. This is pivotal in predicting behavior under loads. Can anyone rewrite this relation?
$Y(s) = \frac{F\{q(x)\}}{EI s^4}$?
Perfect! We've arrived at our key relation that connects the Fourier cosine transform, the applied load, and deflection reversibly.
Inverse Fourier Cosine Transform
Unlock Audio Lesson
To conclude our discussions, let’s talk about deriving the inverse Fourier Cosine Transform to find $y(x)$. Who can tell me why the inverse is important here?
Because we need to find the actual deflection from the transformed function?
Exactly! Through the inverse transform, we convert our frequency domain solution back into the spatial domain to get the actual deflection profile of the beam.
What would the physical meaning of $y(x)$ be?
Great insight! $y(x)$ represents the vertical displacement profile of the beam along its length due to the applied load, which is critical for design considerations.
So if I know the load, I can find out how much the beam bends?
Precisely! This integral solution encapsulates the bridge between theory and practice. Let’s wrap up by summarizing: We applied Fourier Cosine Transform to analyze and find the actual deflection in a cantilever beam, leveraging inverse transforms effectively.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore how the Fourier Cosine Transform is used to derive the deflection of a cantilever beam with a fixed end subjected to a load. The Euler-Bernoulli beam equation is introduced, followed by the application of Fourier transforms to solve for the beam's deflection under given boundary conditions.
Detailed
Application: Beam Deflection with One Fixed End
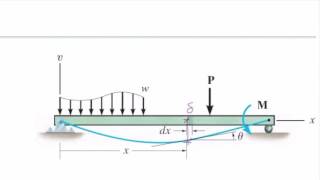
In civil engineering, the deflection of beams is a fundamental problem, especially for cantilever beams which are fixed at one end. In this section, we focus on a cantilever beam of length L that is subjected to a distributed load denoted as q(x).
The governing equation for the beam's deflection comes from the Euler-Bernoulli beam theory and is expressed as:
$$\frac{d^4y}{dx^4} = \frac{q(x)}{EI}$$
where $EI$ is the flexural rigidity of the beam.
Boundary Conditions
Given that the beam is fixed at x = 0, we apply the following boundary conditions:
- $y(0) = 0$ (the deflection at the fixed end is zero)
- $y'(0) = 0$ (the slope at the fixed end is zero)
Application of Fourier Cosine Transform
To solve for the deflection $Y(s) = F\{y(x)\}$ using Fourier Cosine Transform, we apply the transform to both sides of the Euler-Bernoulli equation:
- Taking the Fourier Cosine Transform gives us:
$$ F\{\frac{d^4y}{dx^4}\} = s^4Y(s) $$ - This leads to:
$$ s^4Y(s) = F\{q(x)\} $$ - Rearranging, we find:
$$ Y(s) = \frac{F\{q(x)\}}{EI s^4} $$
Inverse Transform
The deflection of the beam can be derived by taking the inverse Fourier Cosine Transform of $Y(s)$, thereby allowing engineers to determine how the beam reacts under the specified load conditions. This methodology is crucial for predicting structural behavior in practical applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of the Cantilever Beam
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A cantilever beam of length L, fixed at x = 0, subjected to a load q(x).
Detailed Explanation
A cantilever beam is a type of beam that is fixed at one end and free at the other. When subjected to a load q(x), the beam experiences deflection due to this load. The length of the beam is represented as L, and the fixed end is at the point x = 0. Understanding how loads affect the deflection of the beam is crucial in structural engineering to ensure safety and stability.
Examples & Analogies
You can think of a diving board as a cantilever beam. The end where the diver stands (the free end) can bend down when someone jumps on it, while the other end (the fixed end) is secured to the platform.
Euler-Bernoulli Beam Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Euler-Bernoulli beam equation is: \[ \frac{d^4y}{dx^4} = \frac{q(x)}{EI} \]
Detailed Explanation
The Euler-Bernoulli beam equation describes the relationship between the load applied to the beam and the resulting deflection. Here, \(y\) is the deflection of the beam, \(q(x)\) represents the load per unit length, and \(E\) is the modulus of elasticity of the material, while \(I\) is the moment of inertia of the beam's cross-section. The fourth derivative of deflection with respect to x indicates how the curvature of the beam changes along its length, which is critical for understanding deflection behavior.
Examples & Analogies
Imagine the deflection as a bow and arrow. The stiffer the bowstring (like having a high EI), the less it bends under the force you apply. The load q(x) can be thought of as the strength of your pull on the string.
Boundary Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
With boundary conditions (fixed end at x=0): y(0)=0, y′(0)=0.
Detailed Explanation
Boundary conditions are constraints that describe the behavior of the beam at its ends. The condition \(y(0) = 0\) indicates that there is no deflection at the fixed end, meaning it must stay at that point. The second condition \(y'(0) = 0\) means that the slope (or angle) of the beam is also zero at the fixed end, implying that it does not tilt or rotate at this point. These conditions are crucial to accurately solving for the deflection across the length of the beam.
Examples & Analogies
Think of a streetlight pole anchored into the ground. The point where it’s anchored (boundary condition) cannot move at all (y(0)=0) and it stands straight up (y′(0)=0) without tilting.
Applying the Fourier Cosine Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We apply the Fourier Cosine Transform to both sides: Let Y(s)=F {y(x)}, then: \[ F \left\{ \frac{d^4y}{dx^4} \right\} = s^4 Y(s) \].
Detailed Explanation
Applying the Fourier Cosine Transform converts the differential equation in the spatial domain into an algebraic equation in the frequency domain. By denoting \(Y(s)\) as the cosine transform of the deflection function \(y(x)\), we reframe the problem to be easier to solve. The transform of the fourth derivative leads to a multiplication by \(s^4\), changing the equation's structure and facilitating the solution.
Examples & Analogies
Consider getting a math problem simplified into a form that's easier to solve, like turning a complex subtraction problem into addition by breaking it down step by step.
Solving for Deflection
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus, \[ s^4 Y(s) = \frac{F \{ q(x) \}}{EI} \] ⇒ \[ Y(s) = \frac{F \{ q(x) \}}{EI s^4} \]. Taking the inverse transform yields the deflection y(x).
Detailed Explanation
After applying the Fourier Cosine Transform, we found an expression for \(Y(s)\) that relates the transformed deflection to the transformed load. The inverse transformation restores our original function, allowing us to find the deflection \(y(x)\) of the beam in the spatial domain. This inverse process is essential in engineering for determining how structures respond to applied loads.
Examples & Analogies
It's like decoding a message that was encoded in a secret language. Taking the inverse transform is like translating it back to plain language so you can understand how the beam is responding to loads.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Euler-Bernoulli Beam Equation: Governs load response and deflection.
-
Fourier Cosine Transform: Tool for analyzing functions defined on semi-infinite domains.
-
Flexural Rigidity: Product of modulus of elasticity and moment of inertia influencing deflection.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Consider a beam of length L subjected to a uniform load across its length; the deflection can be analyzed using the Fourier Cosine Transform.
-
Using Fourier transforms, the equation $$y(x) = \frac{F\{q(x)\}}{EI s^4}$$ can be inverted to find the beam's deflection profile.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In bending beams, remember well, the load brings down, and deflection tells.
📖 Fascinating Stories
-
Imagine a diver on a diving board; as they jump, the board bends under their weight. Just like beams, the more weight, the more bend.
🧠 Other Memory Gems
-
Use 'BEND' for Beam Deflection: Beam, Elasticity, Nodal analysis, Deflection.
🎯 Super Acronyms
DURL
- Deflection Under Real Loads
- to remember the process steps.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Beam Deflection
Definition:
The displacement of a structural element (a beam) under load.
-
Term: Fourier Cosine Transform
Definition:
A mathematical transform used to express a function defined on a semi-infinite domain in terms of cosine functions.
-
Term: EulerBernoulli Beam Equation
Definition:
A fundamental equation governing the behavior of beams under bending.
-
Term: Flexural Rigidity
Definition:
A measure of a beam's ability to resist bending, expressed as the product of the modulus of elasticity and the moment of inertia.
-
Term: Inverse Transform
Definition:
A process to revert a transformed function back to its original form.