Sine Transform of First Derivative
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Sine Transform
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will learn about the Sine Transform of the first derivative. This transformation helps in simplifying many boundary value problems. Can anyone tell me what a boundary value problem is?

Isn't it a problem where we need to find a solution to a differential equation with specific conditions defined at the boundaries?

Correct! Now, the formula we use is $F \{f′(x)\} = sF \{f(x)\} - f(0)$. This means that we can express the transform of a derivative in terms of the transform of the original function. Who can tell me why this is useful?

It allows us to transform the problem into the frequency domain, making it easier to solve!

Exactly! This transformation is particularly helpful in civil engineering applications, such as analyzing heat conduction. Let’s remember this with the acronym S.T.F.D.: Sine Transform of First Derivative.
Applications in Civil Engineering
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s think about where this transformation could be applied. Can anyone suggest a scenario from civil engineering?

How about in analyzing the deflection of beams?

Yes! If we need to find how a beam deflects under a load, we can apply the Sine Transform to express our equations more simply. Why is it preferable to use the Sine Transform here?

Because the beam can have boundary conditions that fit the requirements for using the Sine Transform.

That's correct! Remember, the Sine Transform is particularly useful when the function is zero at one boundary. Let’s summarize this point: the Sine Transform simplifies deflection problems!
Understanding the Formula
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s break down the formula $F \{f′(x)\} = sF \{f(x)\} - f(0)$ into parts. What does each part represent?

I think $sF \{f(x)\}$ is the Sine Transform of the function itself, adjusted for the frequency.

Right! And what about $- f(0)$?

That part seems to represent the value of the function at the boundary point, which is important when taking the derivative into account.

Exactly! It captures the influence of the function at the boundary. So, we see how the transform accounts for both the alteration in frequency and the original function value. Let's remember this component as the boundary term. Summarizing, understanding the formula helps us see how functions behave under transformations!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The Sine Transform of the first derivative provides a method for transforming derivatives, which helps to simplify many boundary-value problems found in civil engineering, including thermal gradients and beam deflections. This relationship is crucial for solving partial differential equations.
Detailed
Sine Transform of First Derivative
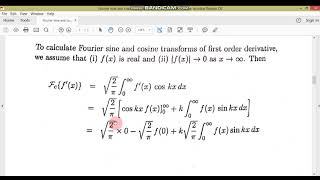
The Sine Transform of the first derivative is expressed mathematically as:
$$ F \{f′(x)\} = sF \{f(x)\} - f(0) $$
This formula is pivotal in transforming functions that involve derivatives, allowing us to address boundary-value problems—common in fields like civil engineering.
Significance
This transformation simplifies complex equations and helps in solving various problems associated with heat distributions, vibrations, and more. It essentially provides an elegant method to handle the behavior of functions that change over space while adhering to specific boundary conditions. By utilizing the Sine Transform, engineers can more easily analyze situations where functions vanish at a boundary, such as one end of a beam or rod. The transformation is thus foundational in the application of Fourier analysis in engineering.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Sine Transform of First Derivative
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
r2
F {f′(x)}=sF {f(x)}− f(0)
s c π
Detailed Explanation
This formula describes how to transform the first derivative of a function f(x) into the frequency domain using the Sine Transform. The left side of the equation represents the Sine Transform of the derivative of f, denoted F {f′(x)}. The right side of the equation indicates that this transform relates to the Sine Transform of the original function f(x), represented as F {f(x)}. Additionally, it accounts for the value of the function at the boundary point, f(0), which affects the result.
Examples & Analogies
Imagine you are tracking the speed of a car (which represents the derivative, f′(x)). The Sine Transform of the speed helps you analyze how the speed behaves over time and at various frequencies. However, the initial speed of the car (f(0)) at the start of your observation period is crucial because it affects your analysis of the car's performance and how it accelerates or decelerates.
Importance in Boundary Value Problems
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
These relations help simplify many boundary-value problems in civil engineering (e.g., thermal gradient, slope in beam deflection).
Detailed Explanation
Understanding the Sine Transform of a derivative is particularly useful in boundary value problems typical in civil engineering. When working with thermal distributions or deflections in beams, the transformation helps convert complex differential equations into simpler algebraic equations in the frequency domain. This simplification enables engineers to solve for unknown variables more easily, making design and analysis more efficient.
Examples & Analogies
Consider an engineer working on a bridge design. The engineer needs to understand how the materials will stretch and compress under various loads (this relates to differential equations). By employing the Sine Transform of derivatives, the engineer can translate these complex relationships into a format that is manageable and can systematically assess how the bridge will behave under different conditions, much like deciphering a complicated recipe into easier steps to follow.
Key Concepts
-
Sine Transform of the First Derivative: A method to transform derivatives to simplify boundary value problems.
-
Boundary Conditions: These are essential constraints defined at the edges of the domain that affect function behavior.
Examples & Applications
Using the Sine Transform of the first derivative allows engineers to calculate deflections in beams under specific loads.
The transformation can also assist in determining temperature distributions in materials subjected to thermal influences.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When derivatives play, the Sine Transform will save the day!
Stories
Imagine an engineer building a bridge. To calculate how it will flex under pressure, they use the Sine Transform of the first derivative.
Memory Tools
Remember the acronym S.T.F.D. for Sine Transform of First Derivative!
Acronyms
S.T.F.D. - Sine Transform, First Derivative.
Flash Cards
Glossary
- Sine Transform
A mathematical operation that transforms a function defined on a semi-infinite interval into its frequency domain representation using sine functions.
- Boundary Value Problem
A differential equation together with a set of additional constraints called boundary conditions.
- Fourier Transform
A mathematical function that transforms a function of time or space into a function of frequency.
Reference links
Supplementary resources to enhance your learning experience.
