Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Inverse Fourier Cosine Transform
Unlock Audio Lesson
Today, we'll discuss the Inverse Fourier Cosine Transform, which helps us recover the original function from its cosine transform.
How exactly does the Inverse Fourier Cosine Transform work?
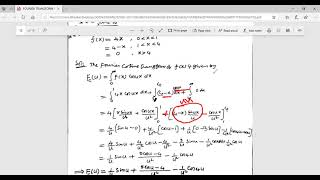
Great question! Typically, if we have a transform function F(s), the inverse transform can be expressed as: $$ f(x) = \frac{2}{\pi} \int_0^{\infty} F(s) \cos(sx) \, ds $$.
What are the conditions for the function f(x) to be valid for this transform?
f(x) must be piecewise continuous on every finite interval in [0,∞) and absolutely integrable over that range.
Can you explain why this transform is particularly useful in civil engineering?
Certainly! It aids in solving boundary value problems which arise frequently in fields such as heat transfer and structural analysis.
To summarize, the Inverse Fourier Cosine Transform is vital for retrieving the original function from its cosine frequency representation, especially in engineering applications.
Applications of the Inverse Fourier Cosine Transform
Unlock Audio Lesson
Let's delve into how the Inverse Fourier Cosine Transform applies in civil engineering.
What kind of problems does it help solve?
For instance, when analyzing heat conduction in a semi-infinite slab, we use this transform for boundary conditions at one end.
What about beam deflection?
Excellent point! The inverse transform can also solve beam bending equations when we know the displacement or slope at a fixed end.
Can you give a practical example?
Of course! A cantilever beam fixed at one end under a load q(x) can be analyzed using the Inverse Fourier Cosine Transform to find the deflection.
In summary, the inverse transform is essential for real-world applications in engineering problems, particularly under specific boundary conditions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explains the Inverse Fourier Cosine Transform, detailing how it is used to recover the original function f(x) from its transform F(s). It covers the mathematical representation and its significance in analyzing problems with certain boundary conditions in civil engineering.
Detailed
Inverse Fourier Cosine Transform
The Inverse Fourier Cosine Transform (IFCT) is an essential tool for recovering original functions from their Fourier Cosine Transforms. Defined mathematically as:
$$ f(x) = \frac{2}{\pi} \int_0^{\infty} F(s) \cos(sx) \, ds $$
where:
- F(s) is the Fourier Cosine Transform of f(x),
- The function f(x) is defined on the semi-infinite domain [0,∞), and is piecewise continuous and absolutely integrable.
This transform is particularly useful in the analysis of boundary value problems, especially within the fields of heat transfer, wave motion, and vibrations, demonstrating its importance in civil engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Inverse Fourier Cosine Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a function f(x) defined on [0,∞), the Inverse Fourier Cosine Transform is defined as:
r2 Z ∞
f(x)= F(s) cos(sx) ds
π c
0
Detailed Explanation
The Inverse Fourier Cosine Transform is a mathematical tool used to retrieve the original function f(x) from its cosine transform F(s). This expression indicates the relationship between the two; by integrating over all frequencies s and weighting by the cosine function, we get back the original function. The integration is done across the semi-infinite domain [0, ∞), which is important for problems related to boundary conditions in physical systems.
Examples & Analogies
Think of this transform like a recipe to recover a cake from its ingredients. Just as you can use a list of ingredients and their proportions to recreate the cake, the inverse cosine transform uses the information from the transformed function (the 'ingredients') to reconstruct the original function (the 'cake').
Purpose of the Inverse Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This restores the original function from its cosine transform.
Detailed Explanation
The main purpose of the Inverse Fourier Cosine Transform is to allow us to convert data, which has been represented in the frequency domain via the Fourier Cosine Transform, back into the original spatial domain. This is crucial in many applications, such as engineering and physics, where we need to analyze and interpret original waveforms or signals from their transformed representations.
Examples & Analogies
Imagine you were listening to a song on the radio but only had the frequency specifications of the signal. The inverse transform is like receiving those specifications and being able to play the original song again. This process is essential to understand how various frequencies contribute to the overall sound of music, just as it applies to signals in engineering.
Application Context
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The inverse transform plays a critical role in various fields including civil engineering, where it is employed to analyze vibrations and waves.
Detailed Explanation
In civil engineering, the Inverse Fourier Cosine Transform allows engineers to analyze the effects of forces, such as vibrations in structures, and recover the original displacement or stress distribution in materials from the frequency domain where they study phenomena like heat conduction or wave propagation. Thus, it’s practical for solving real-world engineering problems that involve boundary conditions.
Examples & Analogies
Consider a bridge vibrating due to traffic. Engineers can use the Inverse Fourier Cosine Transform to figure out the original shapes of these vibrations (displacements) from frequency data, much like using footprints to determine the paths people walked on the bridge. This helps in ensuring the safety and integrity of the structure.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Inverse Fourier Cosine Transform: A key method for retrieving original functions from transforms, essential in solving boundary value problems.
-
Piecewise Continuity: A necessary condition for functions to be applicable in the context of Fourier transforms.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using the Inverse Fourier Cosine Transform to solve the deflection of a cantilever beam under load.
-
Applying the transform to analyze the temperature distribution in a semi-infinite rod.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the Inverse Transform, we find the past, from F back to f, it happens fast.
📖 Fascinating Stories
-
Imagine a detective (the Inverse Transform) piecing together clues (F(s)) to find the original story (f(x)).
🧠 Other Memory Gems
-
FIND - F(s) leads to INverse function by using cosine to Discover original content.
🎯 Super Acronyms
COS - COnvert Signal (F(s)) back to original function (f(x)) using cosine.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Inverse Fourier Cosine Transform
Definition:
A mathematical operation that retrieves the original function f(x) from its Fourier cosine transform F(s), typically applied in civil engineering problems.
-
Term: Boundary Value Problems
Definition:
Mathematical problems in which we determine a function that satisfies certain conditions at the boundaries of its domain.
-
Term: Piecewise Continuous
Definition:
A function that is continuous on each piece of its domain but may have a finite number of discontinuities.
-
Term: Absolutely Integrable
Definition:
A function f(x) for which the integral of its absolute value over its domain is finite.