Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Differentiation in Fourier Cosine Transform
Unlock Audio Lesson
Today we're going to explore how to differentiate functions when we apply the Fourier Cosine Transform. Can anyone tell me what the property of differentiation with FCT states?
Is it that if the function is differentiable, the transform of the derivative has a specific relationship to the transform of the function?
Exactly! The property states that if f(x) is differentiable and tends to zero as x goes to infinity, then the Fourier Cosine Transform of its derivative is equal to -s times the Fourier Cosine Transform of the function itself. This is a vital tool in solving boundary value problems!
Can you break that down a bit more? What does it mean in practical terms?
Sure! This means when we encounter a problem where we need to differentiate a function, we can use this transform property to simplify our calculations significantly. It essentially allows us to convert a continuous function problem into a calculable form in frequency space.
That sounds useful! But how do we apply it to actual problems?
Great question! Let's consider an example: suppose we have a function that describes temperature in a rod. By differentiating through the Fourier Cosine Transform, we can find heat distribution over time.
Can we expect similar properties in the Sine Transform?
Yes! And that leads us seamlessly into the next topic. Now let’s summarize: the key point here is that differentiation via the Fourier Cosine Transform allows us to establish a relationship between the original function and its derivative in the frequency domain.
Differentiation in Fourier Sine Transform
Unlock Audio Lesson
Now, let’s shift our focus to the Fourier Sine Transform. Can anyone summarize how differentiation works for this transform?
Is it that the transform of the derivative can be expressed in terms of the sine transform of the function?
Exactly right! The property states that the Fourier Sine Transform of the derivative of a function f(x) is related to its original transform by an expression involving s, the transform variable. More precisely, it’s s times the transform of f plus the value of f at zero.
What does this mean for boundary value problems?
This property is particularly useful when the function is zero on the boundary, which is ideal for problems like wave equations in strings. It provides a means to compute the behavior of the system at fixed boundaries.
So it sounds like this could help when the displacement vanishes at the boundary?
Yes! By applying this transformation, we can manage those boundary conditions much more effectively. Now let me summarize the key concept: differentiating a function with the Fourier Sine Transform allows us to make use of its properties to simplify the treatment of boundary value problems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on how differentiation is handled within the context of Fourier Cosine and Sine Transforms. It provides formulas, properties, and examples to help students understand how to apply these transforms in various boundary value problems encountered in civil engineering.
Detailed
Detailed Summary
In this section, we explore the crucial role of differentiation in the framework of Fourier Cosine and Sine Transforms, particularly in the realm of boundary value problems pertinent to civil engineering contexts. The section outlines the differentiation properties of both transforms, detailing how derivatives can be computed using the transforms and the implications for solving partial differential equations.
Key Points:
- Differentiation with Fourier Cosine Transform (FCT):
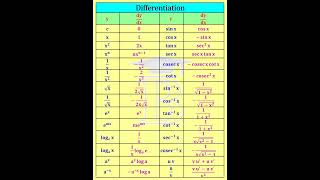
- The property states that if a function f(x) is differentiable and vanishes as x tends to infinity, then the Fourier Cosine Transform of its derivative can be expressed as: $$ F \{f'\}(x) = -s F \{f\}(x) \text{ (using cosine transform)} $$
- Differentiation with Fourier Sine Transform (FST):
- Similarly, for the Fourier Sine Transform, the formula for differentiation is given by: $$ F \{f'\}(x) = s F \{f\}(x) - f(0) \text{ (using sine transform)} $$
- Applications:
- These properties are particularly useful when addressing engineering problems involving thermal gradients, beam deflection, and wave motion, where establishing relationships and simplifying derivatives is essential for solution derivation and practical application.
Understanding these differentiation properties is crucial for engineers and students alike, as it enables the application of Fourier transforms in analyzing and solving real-world engineering problems that involve boundary value conditions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Differentiation in Fourier Sine Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If f(x) is differentiable and vanishes as x→∞,
$$F \{f'(x)\} = s F \{f(x)\} - f(0)$$
Detailed Explanation
This chunk discusses the property of differentiation in the context of the Fourier Sine Transform. It states that if you have a function f(x) that is differentiable and approaches zero as x approaches infinity, you can find the Fourier Sine Transform of its derivative, denoted as f'(x), using the formula provided. The term 's F {f(x)}' indicates a direct relationship between the Fourier Sine Transform of the function and its derivative. Additionally, '−f(0)' signifies that the initial value of the function at x = 0 impacts the transform of the derivative.
Examples & Analogies
Consider a car moving on a road. The function f(x) represents the car's position at any given point in time (x). The derivative f'(x) denotes the car's speed. Now, if we wanted to find out how the speed (derivative) relates to the original position function in terms of frequency (like sound frequency when the car accelerates), the formula provides a way to connect these ideas. Just as the car's starting position (where x = 0) matters in determining its journey, f(0) influences how we understand the car's speed in the frequency domain.
Impact of the Initial Value on the Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The term −f(0) indicates that the initial value of the function at x = 0 impacts the transform of the derivative.
Detailed Explanation
In this chunk, we further elaborate on the significance of the term '−f(0)' in the differentiation formula for the Fourier Sine Transform. This aspect is crucial because it highlights how the behavior of the function at the starting point (x = 0) can substantially influence the entire analysis in the frequency domain. When the initial value is included, it shows that any initial conditions of a system (like temperature or deflection in civil engineering problems) will affect the dynamics of has its response when we analyze it using transforms.
Examples & Analogies
Think about a swimming pool. If the water level starts at a certain height (f(0)), it affects how fast the water can move when someone jumps in (the derivative, f'(x)). If the pool is empty (f(0) = 0), then the splashes and ripples caused by the jump will be different compared to if the pool were full (f(0) > 0). This analogy helps illustrate that the starting conditions of a function significantly influence its behavior—just like lift-off speed for a rocket depends on its initial height above sea level.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fourier Cosine Transform allows for simplification of differentiation in frequency space.
-
Fourier Sine Transform aids in solving problems with vanishing boundary conditions.
-
Differentiation properties bridge the original function with its transform.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Finding the Fourier Cosine Transform of the derivative of a given function.
-
Applying the Fourier Sine Transform to solve a wave equation with fixed boundaries.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When taking the Cosine's rate, just put a minus, don't debate.
📖 Fascinating Stories
-
Imagine a metal rod, heating up, as time flows. As it cools at one end, sine transforms unveil the throes.
🧠 Other Memory Gems
-
To remember FCT for cos, think of -s as the loss when f’ must cross.
🎯 Super Acronyms
D-FCT
- Derivative means Fourier Cosine Transform involves the negative s.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fourier Cosine Transform (FCT)
Definition:
A transformation that decomposes a function into cosine components, useful for functions defined on a semi-infinite domain.
-
Term: Fourier Sine Transform (FST)
Definition:
A transformation that decomposes a function into sine components, particularly applicable for functions with boundary conditions at zero.
-
Term: Differentiation Property
Definition:
The property that connects the transform of a derivative with the transforms of the function itself in both Fourier cosine and sine cases.
-
Term: Boundary Value Problems
Definition:
Problems that seek a solution to differential equations subject to specific conditions at the boundaries.