Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fourier Transforms of Derivatives
Unlock Audio Lesson
Today, we'll explore how derivatives interact with Fourier transforms, a critical aspect for solving engineering problems. Let's start with the Fourier Cosine Transform of a first derivative. Can anyone recall it?
I think it has something to do with the function itself in the transform.
Exactly! It's expressed as F {f'(x)} = -sF {f(x)}. This tells us how taking a derivative modifies the transform. Why do you think this is valuable in engineering?
It could simplify calculations for heat transfer problems or similar scenarios.
Precisely! Let’s remember that the ‘s’ represents frequency, which illustrates how rapidly our function changes.
Exploring the Sine Transform of a Derivative
Unlock Audio Lesson
Now, let's discuss the Fourier Sine Transform. Who can state its formula for a first derivative?
Isn't it F {f'(x)} = sF {f(x)} - f(0)?
That's correct! The additional term, f(0), accounts for the value of the function at zero, which differentiates it from the Cosine Transform. Why do we include f(0)?
It might help with boundary conditions where the function value at zero is significant.
Great observation! Understanding this helps us apply these transforms effectively in engineering applications.
Applications of Transforms of Derivatives
Unlock Audio Lesson
Considering these transforms, how might we apply them to boundary value problems?
For thermal gradients in materials, we might use cosine transforms.
Exactly! And for beam deflections, we can model slopes using sine transforms. What advantages does the frequency domain give us in these contexts?
It allows us to simplify complex differential equations into more manageable forms!
Correct! By transforming our perspective, problems that seem complex in the spatial domain can become straightforward algorithms in the frequency domain.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we delve into the computation of Fourier transforms of derivatives, focusing on both sine and cosine transforms. Understanding these relationships aids in simplifying many boundary value problems and provides engineers with essential tools for analyzing heat gradients and beam deflections.
Detailed
Fourier Transforms of Derivatives
In this section, we examine the specific Fourier transform relationships for derivatives, which are key in solving partial differential equations (PDEs) in the context of engineering applications.
Key Concepts
- Cosine Transform of First Derivative: The Fourier Cosine Transform of the first derivative of a function is given by:
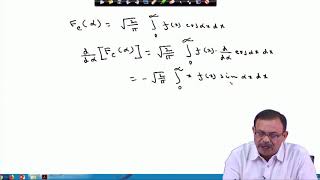
$$ F \{ f'(x) \} = -s F \{ f(x) \}_c $$
- Sine Transform of First Derivative: Similarly, the Fourier Sine Transform of the first derivative is expressed as:
$$ F \{ f'(x) \} = s F \{ f(x) \}_s - f(0) $$
Significance
These formulations simplify the handling of boundary-value problems, particularly in civil engineering applications such as thermal gradients and beam deflection analysis. By understanding how to interact with these derivatives within the frequency domain, engineers can effectively model phenomena encountering these transformations. The use of Fourier transforms allows for a streamlined approach to complex systems that can be expressed in terms of differential equations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Cosine Transform of First Derivative
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
F {f′(x)}=−sF {f(x)}
c s
Detailed Explanation
This formula indicates how the Fourier Cosine Transform relates to the derivative of a function. Specifically, it shows that the transform of the first derivative of a function f(x) is equal to -s times the transform of the function itself. Here, F {f′(x)} is the Fourier Cosine Transform of the derivative, and F {f(x)} is the Fourier Cosine Transform of the original function. The variable 's' represents the frequency domain variable.
This property is particularly useful when solving differential equations as it allows us to know how changes in the function (through its derivative) affect the transforms. It simplifies the process of solving various boundary-value problems by transforming them into algebraic equations in the frequency domain.
Examples & Analogies
Consider a car moving along a straight road where the position of the car over time is represented by the function f(t). The derivative of this function, f′(t), gives us the speed of the car. If we want to analyze the speed in the frequency domain using the Fourier Cosine Transform, this relation shows that knowing the speed directly relates back to our understanding of the position through its transform, allowing engineers to design better traffic systems or safety features.
Sine Transform of First Derivative
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
r2
F {f′(x)}=sF {f(x)}− f(0)
s c π
Detailed Explanation
This formula shows the relationship for the Fourier Sine Transform of the first derivative of a function. It states that the transform of the derivative of the function f(x) is equal to s times the transform of the function f(x) minus the value of the function at zero, f(0). This additional term, -f(0), accounts for initial conditions that might affect how the function behaves at the boundaries of its domain. This relationship is crucial in solving problems where behavior at a boundary point (like temperature or displacement) has significant implications, for example, in heat equations or beam deflections in civil engineering.
Examples & Analogies
Imagine you are measuring the temperature of a long metal rod where one end is heated and held at a specific temperature while the other end is free to change. Here, the f(0) represents the known temperature at the heated end. The speed at which heat spreads along the rod corresponds to the derivative of the temperature function, and understanding how this 'heat speed' translates into the frequency domain helps engineers ensure materials can withstand temperature changes without failing, ensuring safety and durability in construction.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Cosine Transform of First Derivative: The Fourier Cosine Transform of the first derivative of a function is given by:
-
$$ F \{ f'(x) \} = -s F \{ f(x) \}_c $$
-
Sine Transform of First Derivative: Similarly, the Fourier Sine Transform of the first derivative is expressed as:
-
$$ F \{ f'(x) \} = s F \{ f(x) \}_s - f(0) $$
-
Significance
-
These formulations simplify the handling of boundary-value problems, particularly in civil engineering applications such as thermal gradients and beam deflection analysis. By understanding how to interact with these derivatives within the frequency domain, engineers can effectively model phenomena encountering these transformations. The use of Fourier transforms allows for a streamlined approach to complex systems that can be expressed in terms of differential equations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The Fourier Cosine Transform of the first derivative allows engineers to simplify expressions related to heat conduction.
-
The Fourier Sine Transform is crucial for determining the slope in cantilever beam deflections when applying boundary conditions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For cosine's first, it's a negative spree, s times the transform, that's the key!
📖 Fascinating Stories
-
Imagine an engineer named Fourier who, whenever he took a derivative, noticed how the function behaved differently, especially at the boundaries where things could change unexpectedly.
🧠 Other Memory Gems
-
DCS - Derivative Cosine Sine: Remember the relationship of derivatives with their cosine and sine transforms!
🎯 Super Acronyms
FCS = First Cosine Sine Transform for remembering the relationships!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fourier Cosine Transform
Definition:
A mathematical transform used to convert a function from the spatial domain into the frequency domain, focusing on even functions.
-
Term: Fourier Sine Transform
Definition:
A mathematical transform that applies to odd functions, converting a function into the frequency domain, especially useful for functions defined on semi-infinite intervals.
-
Term: Boundary Value Problem
Definition:
A type of differential equation problem where solutions must satisfy specific conditions at the boundaries of the domain.
-
Term: Derivative
Definition:
A measure of how a function changes as its input changes, representing the function's rate of change.