Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Linearity of FCT
Unlock Audio Lesson
Let's discuss the first property of the Fourier Cosine Transform, which is linearity. It tells us that if we have two functions, f(x) and g(x), the transform behaves predictably when we add them together.
So if I understand correctly, we can say that the transform of a combination of functions is the combination of their transforms?
Exactly! We can express it mathematically. If we scale by constants a and b, we write it as F_c{af(x) + bg(x)} = aF_c{f(x)} + bF_c{g(x)}. Who can explain why this is useful?
It allows us to work with more complex functions by breaking them down into simpler parts!
Great summary! Remember, linearity is key when decomposing functions. Now let’s move on to scaling!
Scaling Property
Unlock Audio Lesson
The scaling property allows us to manipulate the variable in our functions. For a scaling factor a greater than zero, we have the relation F_c{f(ax)} = (1/a)F_c{f(x)}.
Does this mean that scaling a function also scales its frequency representation?
Exactly! It modifies the width of the function in the frequency domain. By understanding this relationship, how might engineers apply this concept?
They could adjust the scale of their input functions to study different behavior in response functions, maybe in vibration analysis!
Very relevant application! Scaling is crucial in analyzing diverse physical systems. Let's delve into differentiation next.
Differentiation Property
Unlock Audio Lesson
The differentiation property is also fascinating. It tells us that if f(x) vanishes as x approaches infinity, then we have the relation F_c{f'(x)} = -s F_c{f(x)}.
So, transforming the derivative is as simple as multiplying by -s?
That's right! This property is particularly helpful in solving differential equations. Can someone think of an application for this in engineering?
In structural engineering, when analyzing beam deflections, we deal with derivatives a lot!
Spot on! Differentiation aids in managing these analyses beautifully. Now, let’s conclude with Parseval’s Identity.
Parseval's Identity
Unlock Audio Lesson
Parseval’s Identity links the energy in the time domain with the frequency domain. Mathematically: ∫f(x)²dx= ∫F_c(s)²ds.
This means we can analyze the total energy of the function through either domain?
Exactly! This is particularly useful in signal processing. How so?
We can verify energy preservation, ensuring our transformed data represents the original signal accurately.
Exactly right! Recapping today, we’ve covered linearity, scaling, differentiation, and Parseval’s Identity. Understanding these properties is essential for applying transforms effectively in engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explains four key properties of the Fourier Cosine Transform, which are vital for its applications in boundary value problems. These properties include linearity, allowing combinations of functions; scaling, which permits variable adjustments; differentiation, which relates to derivatives in the transform domain; and Parseval's identity, which relates the energy of the signal in both time and frequency domains.
Detailed
Properties of Fourier Cosine Transform
The Fourier Cosine Transform (FCT) is crucial for solving problems defined on semi-infinite domains, such as in civil engineering applications. This section discusses four significant properties:
- Linearity: This property allows us to express the Fourier Cosine Transform of a linear combination of functions as the corresponding linear combination of their individual transforms. It is mathematically represented as:
$$F_c\{af(x) + bg(x)\} = aF_c\{f(x)\} + bF_c\{g(x)\}$$
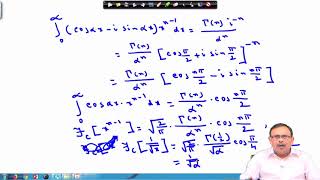
- Scaling: Scaling demonstrates how the transform responds when the independent variable is modified. Formally, for a scaling factor $a > 0$:
$$F_c\{f(ax)\} = \frac{1}{a}F_c\{f(x)\}$$
- Differentiation: This relates the transform of the derivative of a function to the original function transformed. If $f(x)$ is differentiable and vanishes as $x \to \infty$, its Fourier Cosine Transform of the derivative is:
$$F_c\{f'(x)\} = -s F_c\{f(x)\}$$
- Parseval’s Identity: This provides a connection between the total energy of the function in the time domain and its transformed energy in the frequency domain:
$$\int_0^{\infty} f(x)^2 dx = \int_0^{\infty} F_c(s)^2 ds$$
These properties form the backbone of how Fourier Cosine Transforms are applied in solving various civil engineering problems, such as heat conduction and vibrations, by simplifying mathematical computations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Linearity Property
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Linearity:
F {af(x)+bg(x)}=aF {f(x)}+bF {g(x)}
Detailed Explanation
The linearity property of the Fourier Cosine Transform (FCT) states that the transform of a linear combination of functions equals the same linear combination of their transforms. This means that if you have two functions f(x) and g(x), and you create a new function by multiplying f(x) by a scalar 'a' and g(x) by another scalar 'b', the Fourier Cosine Transform of that new function will be the sum of the transforms of the individual functions, scaled by 'a' and 'b'.
Examples & Analogies
Imagine you are adjusting the volume of two different musical instruments in a recording. If you increase the volume of a guitar by 2 times and the volume of a piano by 3 times, the overall sound you hear when you play both instruments together is simply a combination of the guitar's loudness and the piano's loudness. Similarly, in FCT, the contribution of each function to the overall transformation is proportional to its respective scaling factor.
Scaling Property
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Scaling:
F {f(ax)}= F {f(x)} , a>0
Detailed Explanation
The scaling property indicates that if you compress or stretch the input function f(x) by a factor of 'a' (where a is greater than 0), the Fourier Cosine Transform of the scaled function f(ax) will also scale the output of the original transform F {f(s)} accordingly. This means that the effect of expanding the argument of the function just alters the relationship in the frequency domain.
Examples & Analogies
Think of scaling as adjusting the size of a photo. If you take a photo and reduce its dimensions by half, it is a scaled version of the original image. In the context of FCT, scaling changes how 'zoomed in' or 'zoomed out' the representation of the signal appears in the frequency space without changing the core information within that signal.
Differentiation Property
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Differentiation: If f(x) is differentiable and vanishes as x→∞,
F {f′(x)}=−s F {f(x)}sin(sx)dx
Detailed Explanation
This property tells us how to compute the Fourier Cosine Transform of the derivative of a function. If f(x) is a function that can be differentiated and tends towards zero as x approaches infinity, then the transform of its derivative f′(x) can be expressed in terms of the original function's transform. Specifically, it shows how differentiation in the spatial domain corresponds to a modification involving multiplication by 's' and integration involving sine functions in the frequency domain.
Examples & Analogies
Consider the process of tracking a moving car. The position of the car is like the function f(x), while the speed of the car represents the derivative f′(x). This property reveals how knowing the speed (the change in position) gives us significant information about the original position when transformed into frequency space, akin to understanding motion through speed data.
Parseval’s Identity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Parseval’s Identity:
Z ∞ Z ∞
f(x)2dx= F (s)2ds
c
0 0
Detailed Explanation
Parseval’s Identity provides a relationship between the total energy of the function in the spatial domain and its counterpart in the frequency domain. Essentially, it states that the integral of the square of the function f(x) over its domain equals the integral of the square of its transform F(s). This means that the energy or power of the function is preserved across the transformation, highlighting the fundamental nature of the Fourier Cosine Transform in analyzing signals.
Examples & Analogies
Imagine a musician wanting to keep the same level of sound energy whether playing acoustically or electronically. Just as the energy output (how 'loud' the musician plays) must remain the same in both scenarios, Parseval's Identity shows that the total 'energy' of a function is consistent whether observed in space or transformed into frequency.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Linearity: The Fourier Cosine Transform allows the combination of functions in the frequency domain.
-
Scaling: Adjusting the input function scales the transform output, affecting its representation.
-
Differentiation: The transform of a function's derivative can be expressed succinctly, aiding in differential equation solutions.
-
Parseval's Identity: Provides a relationship between the energy of signals in time and frequency domains.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example: If f(x) = x², then F_c{af(x) + bg(x)} = aF_c{x²} + bF_c{g(x)}.
-
Example: Given a function f(ax), its Fourier Cosine Transform relates to the original transform adjusted by 1/a.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Transform to the cosine, so divine, functions combine, energy aligns.
📖 Fascinating Stories
-
Imagine a bridge, its weight balanced perfectly. The forces acting on it are like functions; when you add their effects, you can calculate the resulting stresses using linearity.
🧠 Other Memory Gems
-
LSDP for remembering properties: Linearity, Scaling, Differentiation, Parseval.
🎯 Super Acronyms
FCT
- Fourier Cosine Transform - F represents Fourier
- C: represents Cosine
- T: represents Transform.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fourier Cosine Transform
Definition:
A transformation that converts a function defined on a semi-infinite domain into the frequency domain using cosine functions.
-
Term: Linearity
Definition:
A property that states the transform of a sum of functions equals the sum of their transforms.
-
Term: Scaling
Definition:
A property related to altering the input function that affects the output transform proportional to the scaling factor.
-
Term: Differentiation
Definition:
A property indicating how the transform relates to the derivative of a function.
-
Term: Parseval's Identity
Definition:
A relationship that equates the total energy in the time domain with the total energy in the frequency domain.