Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Linearity of Fourier Sine Transform
Unlock Audio Lesson
Today, we're discussing the linearity of the Fourier Sine Transform. Can anyone tell me what linearity means in the context of transforms?
Does it mean that if we add two functions, the transform will also reflect that addition?
Exactly! Linear functions allow us to express combinations of functions simply. The formula for linearity is F{af(x) + bg(x)} = aF{f(x)} + bF{g(x)}. This allows us to analyze multiple systems together.
So I can scale the output based on the input function weights?
Precisely! Remember, this means we can simplify complex calculations by working with basic components. Great job!
Scaling Property
Unlock Audio Lesson
Now, let's explore the scaling property. What do you think happens when we scale a function in the spatial domain?
I guess the frequency representation changes, but how exactly?
Great question! It’s expressed as F{f(ax)} = (1/a)F{f(s/a)}, meaning we need to adjust the frequency domain by a factor of a. Can anyone relate that to a real-world scenario?
In engineering, scaling a structure will affect its stress distribution!
Exactly, that’s a perfect application! Scaling allows us to predict behavior under different load conditions.
Differentiation Property
Unlock Audio Lesson
Let’s talk about how differentiation works within the Fourier Sine Transform. What can we deduce when we differentiate a function?
The transform of the derivative should somehow reflect the original function's transform?
Exactly! The rule is F{f'(x)} = sF{f(x)} - f(0). Anyone think of a situation where this matters?
When dealing with beams and how bending varies! The ends are key because of boundary conditions!
Spot on! Remember that the behavior at the boundary plays a critical role in structural analysis.
Parseval’s Identity
Unlock Audio Lesson
Lastly, let's examine Parseval's Identity. Who can explain its importance?
It shows that the 'energy' in the time domain equals the 'energy' in the frequency domain?
Exactly! This principle allows us to analyze system stability in both domains. Does that sound useful?
Yes, especially in signal processing or structural integrity checks!
Correct! It emphasizes conservation principles, which are fundamental in engineering design.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section outlines the fundamental properties of the Fourier Sine Transform, such as linearity, scaling, differentiation, and Parseval’s identity. These properties facilitate the transformation of functions from the spatial to the frequency domain, which are essential for solving boundary value problems in civil engineering.
Detailed
Properties of Fourier Sine Transform
The Fourier Sine Transform (FST) is instrumental in converting functions defined on semi-infinite domains into the frequency domain. This transformation provides several properties that are vital for applications, especially in civil engineering.
Key Properties of FST:
- Linearity:
The FST of a linear combination of functions is the linear combination of their transforms:
$$ F\{af(x) + bg(x)\} = aF\{f(x)\} + bF\{g(x)\} $$
This property confirms that the transform respects addition and scalar multiplication, emphasizing the idea that transforms are linear operations.
- Scaling:
The FST for a compressed or expanded function scales appropriately in the frequency domain:
$$ F\{f(ax)\} = \frac{1}{a}F\left\{f\left(\frac{s}{a}\right)\right\}, \quad a > 0 $$
This is significant in adjusting the frequency scale when analyzing different properties of a system.
- Differentiation:
For differentiable functions that vanish at infinity, the transform relates to the derivative of the function:
$$ F\{f'(x)\} = sF\{f(x)\} - f(0) $$
This characteristic is vital when focal points, such as initial conditions or boundary behaviors, are defined.
- Parseval’s Identity:
This shows the equivalence of energy in both time and frequency domains:
$$ \int_0^{\infty} f(x)^2 dx = \int_0^{\infty} |F(s)|^2 ds $$
This identity is crucial in confirming that both domains encapsulate the same physical phenomena, allowing for energy conservation principles in transformations.
Understanding these properties not only facilitates the computation in engineering contexts but also enhances the ability to solve complex differential equations encountered in practical applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Linearity Property
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Linearity:
F {af(x)+bg(x)}=aF {f(x)}+bF {g(x)}
Detailed Explanation
The linearity property states that the Fourier Sine Transform of a linear combination of functions is equal to the same combination of their Fourier Sine Transforms. This means if you have two functions, f(x) and g(x), and you scale them with constants a and b, then the Fourier Sine Transform will also scale accordingly. For example, if you transform af(x) and bg(x) separately and then add them, you will get the same result as performing one transform on af(x)+bg(x). This is useful because it allows us to analyze complex signals by breaking them down into simpler parts.
Examples & Analogies
Think of linearity like mixing colors. If you take red paint and blue paint and make a new color (purple) by combining them in certain proportions, you can also create purple by adjusting the amounts of red and blue in different ratios. Similarly, the Fourier Sine Transform allows us to mix signals and analyze their components individually, just like mixing colors.
Scaling Property
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Scaling:
F {f(ax)}= F , a>0
s a s a
Detailed Explanation
The scaling property indicates how the Fourier Sine Transform behaves when we scale the input function by a positive factor 'a'. When we stretch or compress the input function along the x-axis by a factor of 'a', the transform will reflect this change by adjusting the frequency variable s accordingly, resulting in a new transform. Specifically, if you scale the input by 'a', the output frequency will also change, giving you insights into how the properties of the original function are altered under scaling.
Examples & Analogies
Imagine you have a camera and you zoom in on a landscape. The objects in your view get larger and more detailed, but they take up less of the overall frame in your photo. In a similar way, scaling the function affects how we perceive its frequency components in the Fourier Sine Transform.
Differentiation Property
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
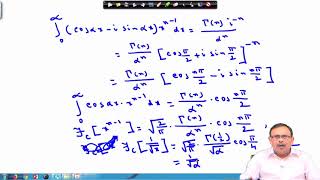
- Differentiation: If f(x) is differentiable and vanishes as x→∞,
F {f′(x)}=s f(x)cos(sx)dx
Detailed Explanation
This property relates the Fourier Sine Transform of the derivative of a function to the Fourier Sine Transform of the function itself. It shows that if f(x) is differentiable and approaches zero as x approaches infinity, the transform of its derivative is directly tied to the function’s transform. Using this property simplifies many differential equations because it allows us to translate operations in the time domain (like differentiation) into simpler algebraic manipulations in the frequency domain.
Examples & Analogies
Consider a speedometer in a car measuring your speed. If you take the derivative of your position over time, you're actually measuring your speed. Now imagine the transform allows you to switch from thinking about the speed (differentiation) to your overall movement profile (the original function). This switch can help engineers and scientists solve problems more easily.
Parseval’s Identity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Parseval’s Identity:
Z ∞ Z ∞
f(x)2dx= F (s)2ds
s
0 0
Detailed Explanation
Parseval's identity is a crucial result connecting the time domain and frequency domain representations of signals. It states that the total energy of the function in the time domain (integrating the square of f(x)) is equal to the total energy in the frequency domain (integrating the square of F(s)). This means we can analyze the energy distribution of a system either in the original measure (time domain) or in its transformed measure (frequency domain), which often simplifies various physics and engineering calculations.
Examples & Analogies
Think of it like the total caloric intake versus caloric expenditure in a diet. The total calories consumed (in your diet-example) reflect your energy input, analogous to the time domain energy. On the other hand, the total calories burned during activities represent your output, analogous to the frequency domain. Both values measure the same energy but in different contexts, much like how Parseval's identity connects these two domains.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Linearity: The linearity property of FST allows for the transformation of sums of functions, simplifying the analysis of complex systems.
-
Scaling: The scaling property helps understand how compressing or expanding functions in the spatial domain affects their representation in the frequency domain.
-
Differentiation: The relationship between differentiation and the Fourier transform is vital for analyzing the change in physical systems.
-
Parseval’s Identity: This identity confirms that the concept of energy is preserved between the spatial and frequency domains, allowing for comprehensive analysis.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of calculating the FST of a simple function, illustrating how to apply the linearity property.
-
Parseval's identity example that shows energy conservation between two different domains.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Sines and cosines, dancing tight; / Energy stays, in day or night.
📖 Fascinating Stories
-
Imagine a city where lights represent energy. When a wave moves, every light adjusts but the total brightness never changes, illustrating energy conservation.
🧠 Other Memory Gems
-
LSDP: Linearity, Scaling, Differentiation, Parseval – main properties of the Fourier Sine Transform.
🎯 Super Acronyms
FST-PSD
- FST properties signify the importance of linearity
- scaling
- differentiation
- and Parseval’s identity.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fourier Sine Transform
Definition:
A mathematical transform used to analyze functions defined on semi-infinite domains by converting them into the frequency domain using sine functions.
-
Term: Linearity
Definition:
A property indicating that a linear combination of functions corresponds to a linear combination of their transforms.
-
Term: Scaling
Definition:
The property that describes how a function's transformation behaves under expansion or compression in the spatial domain.
-
Term: Differentiation
Definition:
The operation of computing the derivative of a function, which has a specific relationship in Fourier transforms.
-
Term: Parseval’s Identity
Definition:
A mathematical identity that expresses the equivalence of the integral of the square of a function in the spatial domain to that in the transform domain.