Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Derivatives in Transforms
Unlock Audio Lesson
Today, we will explore how derivatives are related to Fourier transforms, specifically focusing on the cosine transform of the first derivative. Can anyone remind me of the basic form of a Fourier Transform?
Isn't it F(f(x)) = integral of f(x) multiplied by e^(-isx)?
Exactly! Now, when we introduce differentiation, we need to consider how it interacts with transformations. Do you remember that for the cosine transform of a function, we have a specific representation?
Yes, it's the integral of f(x) cos(sx) dx.
Well done! Now, applying differentiation, we find that the cosine transform of the first derivative is given by F {f'(x)} = -sF {f(x)}. Can anyone explain why we introduce the negative sign?
Is it because we’re looking at a derivative, which indicates a change in direction?
Nice insight! The negative sign reflects the nature of the transformation with respect to frequency. Let's summarize: we transform derivatives into a different domain, which simplifies our analyses.
Applications in Civil Engineering
Unlock Audio Lesson
Now that we've established the theory, let’s connect this to civil engineering applications. Why might we use the cosine transform of the first derivative in analyzing thermal gradients?
Because we often deal with heat conduction problems where temperature gradients are important?
Correct! This transformation allows us to express changes in temperature—modeled by derivatives—in a frequency domain, making complex calculations more manageable. Can anyone think of a specific boundary condition where this is applicable?
A cantilever beam subjected to heat could be an example!
Exactly right! The analysis of deflections in beams under heat can often lead to expressions involving the cosine transform of derivatives.
Benefits of Using Transforms
Unlock Audio Lesson
Let’s discuss the benefits of using Fourier transforms, particularly for derivatives. What advantages do you think we gain when we utilize these transforms?
They simplify differential equations into algebraic ones, making them easier to solve!
Absolutely! It transforms our equations into a form where we can apply algebraic techniques, enhancing computational efficiency. What about the interpretation of results?
It helps to understand how different frequency components contribute to the overall behavior of the system!
Indeed! Each frequency carries unique information about the physical system we’re analyzing. Could someone explain what the relationship between f(x) and f'(x) might indicate in practical scenarios?
The original function may represent something like displacement, while the derivative could represent the slope or rate of change!
Great connection! Understanding these relationships is crucial for applying this knowledge in real-world engineering scenarios.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The cosine transform of the first derivative is presented as a powerful tool in solving boundary-value problems. The relationship is defined as F {f′(x)} = −sF {f(x)}. This transformation is essential in various applications involving mechanical vibrations and thermal gradients.
Detailed
Cosine Transform of First Derivative
The cosine transform of the first derivative of a function is crucial in mathematical and engineering analyses, particularly in boundary-value problems. The formal relationship is given by:
$$ F {f'(x)} = -s F {f(x)} $$
This equation indicates that the cosine transform of the derivative is proportional to the negative frequency multiplied by the cosine transform of the original function. Understanding this relationship helps in effectively solving partial differential equations (PDEs) found in civil engineering, particularly involving the thermal gradient in materials and the slope in beam deflection.
Notably, such transformations simplify calculations and enable engineers to derive meaningful solutions in scenarios where direct analysis may be complex. The implications of this concept extend into various applications including vibrations, heat conduction, and structural analysis.
Youtube Videos
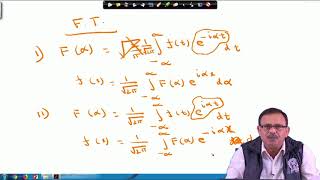
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of the Cosine Transform of the First Derivative
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
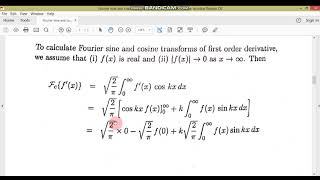
F {f′(x)}=−sF {f(x)}
c s
Detailed Explanation
This formula expresses how the cosine transform interacts with the first derivative of a function. Specifically, it states that the cosine transform of the derivative of a function f(x) can be represented as the negative product of the transform variable 's' and the cosine transform of the function itself, F {f(x)}. It's a key result because it simplifies operations involving derivatives when performing cosine transforms.
Examples & Analogies
Imagine you are analyzing the slope of a hill using a map. The height of the hill at various points can be thought of as f(x). If you want to understand how steep the hill is at various points (the derivative, f′(x)), this formula helps you convert that slope information directly into the transformed frequency domain, which can make further engineering calculations easier.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Cosine Transform of First Derivative: Defined as F {f'(x)} = -sF {f(x)}, useful in engineering analyses.
-
Application in Boundary-Value Problems: Essential for simplifying heat conduction and deflection problems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The cosine transform of a specific function can simplify the analysis of its first derivative, illustrating changes in physical systems over a specified domain.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When differentiation comes into play, the cosine transform leads the way!
📖 Fascinating Stories
-
Imagine an engineer solving a thermal gradient, using the cosine transform to unravel the mystery of temperatures as they climb or descend within materials.
🧠 Other Memory Gems
-
D - Derivative leads to T - Transform, leading to R - Result in frequency.
🎯 Super Acronyms
TFD
- Transform First Derivative!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fourier Transform
Definition:
A mathematical transform that converts a function from the time or spatial domain into the frequency domain.
-
Term: Cosine Transform
Definition:
A specific type of Fourier Transform that is defined for functions on a semi-infinite domain and involves cosine functions.
-
Term: First Derivative
Definition:
A measure of how a function changes as its input changes, indicating the slope of the function.
-
Term: Boundaryvalue Problems
Definition:
Problems that solve differential equations subject to specific conditions at the boundaries of the domain.