Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Circular Membrane Models
Unlock Audio Lesson
Today, we're discussing circular membranes, like the ones used in drums. They vibrate when struck, producing sound. How many of you have seen a drum before?
I have! The surface vibrates and makes a sound when you hit it.
Exactly! And to analyze their vibrations, we use polar coordinates. Can anyone tell me what polar coordinates are?
Polar coordinates describe a point in a plane using a distance from a reference point and an angle.
Right! In this case, the radial distance is denoted as 'r' and the angle as 'θ'. This helps us model the circular membrane. Let’s dig deeper into the wave equation that describes it.
Derivation of the Wave Equation
Unlock Audio Lesson
The two-dimensional wave equation captures how membranes vibrate. In polar coordinates, it changes to include terms accounting for radial and angular displacements.
Can you show us the equation?
Certainly! It looks like this: \[ \frac{\partial^{2}u}{\partial t^{2}} = c^{2} \left( \frac{\partial^{2}u}{\partial r^{2}} + \frac{1}{r}\frac{\partial u}{\partial r} + \frac{1}{r^{2}}\frac{\partial^{2}u}{\partial \theta^{2}} \right) \]. Each term plays a role in how we understand the vibrations.
What do the terms mean?
Good question! The first part with \( c^{2} \) represents wave speed, while the others denote how the displacement varies with radius and angle. Let’s simplify this for axisymmetric vibrations.
What simplification do we make?
We assume that the displacement only depends on 'r' and 't', leading to \[ \frac{\partial^{2}u}{\partial t^{2}} = c^{2} \left( \frac{\partial^{2}u}{\partial r^{2}} + \frac{1}{r}\frac{\partial u}{\partial r} \right) \]. This is simpler and focuses on radial vibrations.
Bessel Functions and Natural Frequencies
Unlock Audio Lesson
After simplifying, we arrive at Bessel's equation. Why do Bessel functions matter in this scenario?
Bessel functions help solve the differential equations for circular membranes, right?
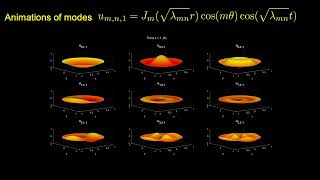
Exactly! The solution involves Bessel functions: \( R(r) = J_n(\alpha r) \). They indicate how the membrane resonates.
What are natural frequencies then?
Natural frequencies are the specific frequencies at which a system tends to oscillate. For circular membranes, these are derived from the zeros of Bessel functions, dictating how they respond to disturbances.
So each mode of vibration corresponds to a natural frequency?
Yes, and understanding these frequencies is crucial for designing structures that use circular membranes effectively.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The Circular Membrane Model section details how circular membranes, like drums, can be mathematically modeled using polar coordinates. It introduces the governing two-dimensional wave equation adjusted for circular geometries, leads to Bessel's equation, and discusses the importance of Bessel functions and natural frequencies in this context.
Detailed
Circular Membrane Model (Polar Coordinates)
In this section, we delve into the behavior of circular membranes, which are relevant in fields like civil engineering, acoustics, and material sciences. For modeling such membranes, polar coordinates (r, θ) are employed to adapt the two-dimensional wave equation, allowing us to capture their dynamic response.
The two-dimensional wave equation for the circular membrane is modified to take into account the structure's geometry. Specifically, the equation transforms to:
\[ \frac{\partial^{2}u}{\partial t^{2}} = c^{2} \left( \frac{\partial^{2}u}{\partial r^{2}} + \frac{1}{r}\frac{\partial u}{\partial r} + \frac{1}{r^{2}}\frac{\partial^{2}u}{\partial \theta^{2}} \right) \]
Under the assumption of axisymmetric vibrations, where the displacement depends only on r and t, the equation simplifies further to:
\[ \frac{\partial^{2}u}{\partial t^{2}} = c^{2} \left( \frac{\partial^{2}u}{\partial r^{2}} + \frac{1}{r}\frac{\partial u}{\partial r} \right) \]
This leads to a vital transformation—a reduction to Bessel's equation, a type of differential equation often encountered when solving problems involving circular symmetries.
The general solution to the wave equation involves Bessel functions:
\[ R(r) = J_n(\alpha r) \]
where \( J_n \) is a Bessel function of order n, and these functions help characterize the modes of vibration of the circular membrane. The zeros of these functions provide the natural frequencies, which indicate how the membrane will vibrate in response to disturbances.
Overall, understanding the circular membrane model is key to predicting the behavior of membranes in various engineering applications, and the utilization of polar coordinates streamlines the analysis significantly.
Youtube Videos
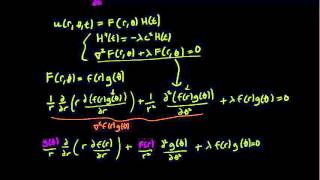
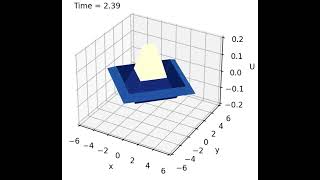
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Circular Membrane Model
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For membranes like circular drums, we use polar coordinates (r,θ). The 2D wave equation becomes:
∂²u / ∂t² = c² (∂²u / ∂r² + (1/r) ∂u / ∂r + (1/r²) ∂²u / ∂θ²)
Detailed Explanation
In this chunk, we introduce the circular membrane model used to analyze the vibration of circular membranes. Instead of using Cartesian coordinates (x, y), we use polar coordinates (r, θ) because they are more suitable for circular shapes. The wave equation describes how waves propagate in the membrane, considering both time and the position within the radius (r) and angle (θ). The equation shows that the acceleration of the membrane's displacement (∂²u / ∂t²) is related to its curvature in the radial direction (∂²u / ∂r²) and angular direction (∂²u / ∂θ²), scaled by constants that reflect the physical properties of the membrane (speed of wave propagation, c).
Examples & Analogies
Think of a drum or any circular membrane. When you hit a drum, it vibrates in a complex way. Instead of describing this vibration using x and y coordinates, which can be difficult for round shapes, we use r (distance from the center) and θ (angle). This makes it easier to understand how sound waves move through the drum.
Assuming Axisymmetric Vibration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Assume axisymmetric vibration: u=u(r,t)
This leads to Bessel’s equation in space:
d²R / dr² + (1/r) dR / dr + (λr²)R = 0
Detailed Explanation
In this chunk, we simplify our analysis by assuming that the vibration of the membrane is axisymmetric, meaning that the displacement only depends on the distance from the center (r) and time (t), not on the angle (θ). This simplification allows us to reduce the complex wave equation to a single variable spatial problem. The result is called Bessel's equation, which arises frequently in problems involving circular or cylindrical symmetry. Here, λ is a parameter related to the natural frequencies of the system.
Examples & Analogies
Imagine a merry-go-round where everyone is holding hands in a circle and moving up and down. Their movement can be described just by how far they are from the center and how their position changes over time, rather than worrying about their specific angles. This is similar to how we analyze the vibrations of a circular membrane.
Solution Involving Bessel Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The solution involves Bessel functions:
R(r) = J_n(α r)
where n are zeros of J_0. This gives natural frequencies for circular membranes.
Detailed Explanation
In this chunk, we discuss the solutions to Bessel’s equation. The displacement function R(r) is expressed in terms of Bessel functions, denoted as J_n, which are special functions that naturally arise in problems of circular symmetry. The parameter α determines the specific modes of vibration, which correspond to the 'natural frequencies' of the membrane. These are the frequencies at which the circular membrane vibrates most easily, resulting in distinct sound patterns.
Examples & Analogies
Consider a circular pond when you throw a stone in it. The ripples that spread out can be likened to the natural vibrating modes of a circular membrane. Each ripple pattern corresponds to different vibrational shapes the membrane can take, much like how different musical notes are produced when striking the drum at different spots.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Polar Coordinates: Used to model circular membranes, represented by radius and angle.
-
Wave Equation: Governs the behavior of vibrating membranes, adapted in this context to fit circular shapes.
-
Bessel Functions: Mathematical functions that solve circular differential equations, determining vibration modes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
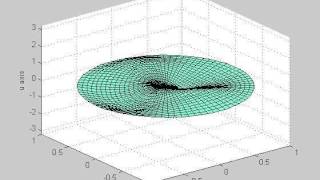
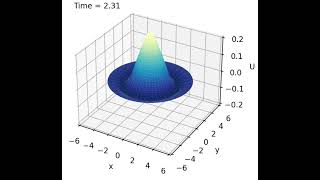
A drum vibrating when struck shows a circular membrane in action. Its vibrations are modeled using the two-dimensional wave equation in polar coordinates.
-
The natural frequencies of a circular membrane can be calculated using the zeros of Bessel functions, illustrating how they resonate.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a circular form, the waves do play, With polar coordinates leading the way!
📖 Fascinating Stories
-
Imagine a drum in a circus, where the juggler strikes. The vibrations form waves that echo like bikes. With polar coordinates, we chart the sound, The rhythm of vibrations, perfectly found.
🧠 Other Memory Gems
-
Remember Bessel functions for waves and their needs, 'B' is for Boundaries, 'E' for Energy, and 'S' for Solutions to make the sound lead!
🎯 Super Acronyms
CIRCLES
- C: for Circular
- I: for Inclination
- R: for Radii
- C: for Waves
- L: for Length
- E: for Energy
- S: for Symmetry in vibration.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Circular Membrane
Definition:
A thin, flexible surface shaped in a circular form that vibrates when disturbed.
-
Term: Polar Coordinates
Definition:
A coordinate system that represents a point in a plane using a radius and angle.
-
Term: Bessel Function
Definition:
Special mathematical functions that appear in the solution of differential equations with circular symmetry.
-
Term: Natural Frequency
Definition:
The frequency at which a system naturally tends to oscillate when not subjected to external forces.
-
Term: Wave Equation
Definition:
A partial differential equation describing the propagation of waves through a medium.