Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Square Membrane Vibration
Unlock Audio Lesson
Today, we'll talk about the vibration of a square membrane. Can anyone tell me how we define the natural frequencies in this case?
I think the frequency is related to the dimensions of the membrane.
Exactly! For a square membrane, its natural frequencies can be defined using a formula that involves the tension and dimensions of the membrane. Specifically, we write it as ω = cπ√(n² + m²)/a.
What do the variables n and m represent?
Great question! The variables n and m refer to the mode numbers indicating specific symmetrical or asymmetrical vibration patterns of the membrane.
Could you explain what those patterns look like?
Sure! Patterns like (1,1) create the fundamental mode, while (2,1) and (1,2) show more complex shapes. Each mode affects how the membrane behaves during vibration.
In summary, for square membranes, understanding these modes and frequencies is crucial for applications in civil engineering.
Initial Displacement Scenario
Unlock Audio Lesson
Now, let's move on to our second example which considers initial displacements. Who can remind us what happens when we set up initial conditions?
Setting the initial displacement determines how the membrane will start vibrating.
Exactly! If we assume initial vertical displacement u(x,y,0)=f(x,y) and initial velocity ∂u/∂t(x,y,0)=0, what can we conclude about the coefficients A_nm?
All B_nm coefficients will be zero since there’s no initial velocity, right?
Correct! This simplifies our analysis greatly. We then compute the coefficients A_nm using integrals of the initial displacement function.
So does that mean the behavior is entirely based on the initial shape?
Exactly! The initial conditions set the stage for how the membrane vibrates later on. Understanding this principle is essential in engineering.
To summarize, different conditions impact how membranes vibrate, and analyzing those impacts is critical in practical scenarios.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores specific cases of vibrating membranes, particularly focusing on a square membrane and different initial displacement scenarios, detailing how these vibrations can be quantified and understood using natural frequencies and modes of vibration.
Detailed
Detailed Summary
This section provides practical examples of membrane vibrations, focusing on two main cases. The first example considers a square membrane, where the natural frequencies are simplified to relate directly to the square shape. For modes of vibration, combinations such as (1,1), (2,1), and (1,2) are discussed, showcasing how different patterns arise during vibration.
The second example illustrates a scenario with specific initial displacement settings, where only initial positions affect the outcome, resulting in certain coefficients being zero. This leads to the integration that determines the amplitude of vibration based on defined functions. Overall, understanding these examples aids in practical applications in civil engineering, emphasizing how foundational theories can be applied to solve real-world problems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
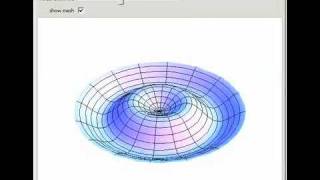
Example 1: Square Membrane
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let a=b. The natural frequencies simplify to:
cπ
ω = √n² + m²
nm a
Modes such as (1,1), (2,1), (1,2), etc., show symmetric and asymmetric patterns of vibration.
Detailed Explanation
In this chunk, we discuss the example of a square membrane, where the dimensions are equal (a=b). This simplifies our calculations of natural frequencies, which are important for understanding how the membrane vibrates. The formula given shows how the natural frequency (ω) depends on the mode numbers n and m. Each pair (n,m) corresponds to a specific pattern of vibration known as a 'mode'. For instance, the modes (1,1), (2,1), and (1,2) represent different vibration patterns—some of which may appear symmetrical and others asymmetrical with respect to the center of the membrane.
Examples & Analogies
Think of a drum. When you hit a drumhead, it vibrates in different ways depending on where you hit it. The fundamental sound you hear is the lowest frequency, which corresponds to the (1,1) mode. If you hit it harder on one side, you might notice more complex sounds, similar to the (2,1) or (1,2) modes—some parts of the drum vibrate more than others, creating a richer sound.
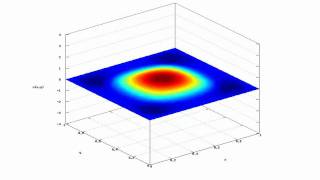
Example 2: Initial Displacement Only
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Suppose u(x, y,0)=f(x,y),
∂u
(x, y,0)=0 . Then all B nm=0 , and:
a b
4 (nπ x) (mπ y)
A = ∫∫f(x,y)sin sin d xd y
nm ab a b
0 0
Detailed Explanation
In this example, we consider a membrane that is displaced at time t=0 according to a specific shape given by the function f(x,y). The condition ∂u/∂t = 0 indicates that the membrane starts from rest—meaning it wasn't moving at that moment. The constant B_n_m, which governs oscillations, becomes zero under this condition. The coefficient A_n_m is then calculated using a double integral, where the term captures the initial shape of the membrane. This helps us establish the specific initial conditions that can lead to the resultant vibration modes of the membrane over time.
Examples & Analogies
Imagine stretching a piece of fabric and then letting it go. As it snaps back into place, it might not just return to its original shape; it could ripple or undulate based on how you initially pulled or pushed it. The initial shape is the key factor influencing how it will bounce back or vibrate afterward.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Square Membrane: A rectangle in the xy-plane whose natural frequencies depend on its dimensions and tension.
-
Initial Conditions: The setup of a vibrating system concerning the initial displacement and velocity, which determines the behavior of vibrations.
-
Patterns of Vibration: Asymmetric and symmetric modes arise based on natural frequencies and configurations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: The square membrane vibrates with natural frequencies determined by the formula ω = cπ√(n² + m²)/a.
-
Example 2: Initial displacement only affects vibrations based on defined functions for amplitude, leading to unique patterns.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When the membrane starts to sway, frequencies come out to play!
📖 Fascinating Stories
-
Imagine a drum head that vibrates in different ways, each mode dancing with the tension and space.
🧠 Other Memory Gems
-
F.O.R.M. - Frequencies, Oscillation, Resonance, Modes help remember key properties of vibrating membranes.
🎯 Super Acronyms
M.I.N.D. - Modes Indicate Natural Dynamics, a key concept in understanding vibrations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Natural Frequency
Definition:
The frequency of free vibrations of a system without any external forces acting on it.
-
Term: Mode of Vibration
Definition:
A specific pattern of vibration characterized by a fixed shape over time.
-
Term: Initial Displacement
Definition:
The initial position of points on a vibrating body before any motion starts.