Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Vibrating Membrane
Unlock Audio Lesson
Today, we are going to explore the physical model of a vibrating membrane, like a drumhead. What characteristics do you think a membrane might have?
I think it should be thin and flexible?
And it should be stretched tightly across something, right?
Exactly! A membrane must be both thin and under tension. When it vibrates, it can create complex patterns based on how it is disturbed. Can anyone guess what influences these vibration patterns?
Is it the amount of force applied or the way it's fixed at the edges?
Yes, both the initial force and the boundary conditions play significant roles in how the membrane vibrates. Speaking of boundaries, let's discuss what we mean by the membrane's domain!
Boundary Characteristics of Membranes
Unlock Audio Lesson
Our membrane is situated in the xy-plane with the coordinates ranging from 0 to a along the x-axis and 0 to b along the y-axis. Why do we need to discuss its boundaries?
To define where the vibration occurs, I guess?
Correct! In our modeling, we assume the membrane is fixed on all edges. This means that the displacement at the boundaries is always zero. Why is this important?
Because if the edges move, the pattern changes, right?
Exactly! A fixed boundary maintains the integrity of the vibration patterns we analyze.
Assumptions in Membrane Analysis
Unlock Audio Lesson
Let’s now discuss some key assumptions in our analysis. First, what do we mean when we say the membrane is homogeneous and isotropic?
Does it mean the material is the same everywhere?
Precisely! It helps simplify our calculations later on. Also, we assume the tension is uniform. Why is tension important?
I think it affects how tightly the membrane vibrates.
Exactly! Uniform tension ensures predictable behavior in our vibration models. Lastly, remember we consider small motions here, which enables us to use linearization.
Free Vibration Concept
Unlock Audio Lesson
Now let’s touch on the concept of free vibration. What does it mean when we say there are 'no external forces acting' on the membrane?
It’s just vibrating on its own without any pushes or pulls?
Correct! This simplifies our model significantly. Does anyone have examples of structures where we might observe this behavior?
Like a drum or a taut piece of cloth?
Yes! Both examples exhibit free vibration under certain conditions, helping us understand their dynamic response.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores the nature of a vibrating membrane, defining its key characteristics, including being a thin, flexible surface under tension. It discusses the assumptions made about the membrane's properties and outlines how external forces and boundary conditions influence its motion.
Detailed
Detailed Summary
This section presents a comprehensive overview of the physical model underlying vibrating membranes, such as those used in engineering contexts (e.g., bridges, architectural fabrics). Key points include:
- Definition and Characteristics: A membrane is identified as a thin, flexible surface that is tightly stretched across a frame, akin to a drumhead. This enables it to vibrate in various complex patterns depending on forces applied, boundary conditions, tension, and mass of the membrane.
- Geometric Representation: The focus is on a rectangular membrane defined within the coordinates of the xy-plane, spending specific attention on its dimensions spanning from 0 to a (x-axis) and from 0 to b (y-axis).
- Displacement Representation: The vertical displacement of the membrane at any position (x,y) over time t is denoted as u(x,y,t).
- Assumptions: Certain assumptions simplify the modeling of the membrane's motion:
- The membrane is homogeneous and isotropic, meaning its properties are uniform in all directions.
- Tension (T) is uniform across the entire surface.
- The analysis focuses on small oscillations, allowing for linear approximations.
- External forces are not considered during the free vibration, making the analysis cleaner and more straightforward.
This foundation is crucial for understanding the two-dimensional wave equation that governs the behavior of the membrane.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of a Vibrating Membrane
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
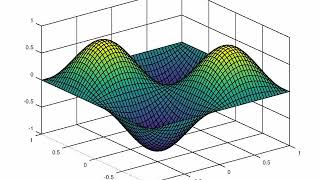
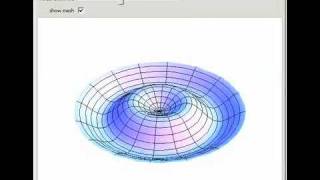
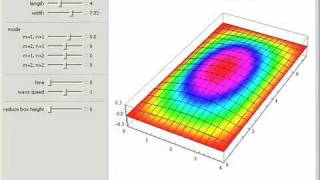
A membrane is a thin, flexible surface stretched tightly across a frame—like a drumhead. When disturbed, it vibrates in complex patterns depending on the initial force, boundary constraints, and its tension and mass.
Detailed Explanation
A vibrating membrane can be thought of as a thin sheet (like the surface of a drum) that is stretched tightly across a frame. When it is hit or disturbed, it doesn’t just move up and down uniformly; rather, it vibrates in various patterns. These patterns can change based on different factors like how hard it is hit, how it is held at the edges (the boundary constraints), and the characteristics of the membrane itself (its tension and mass). This complex behavior is essential in understanding how such materials react to forces.
Examples & Analogies
Consider a drum. When you strike it, the surface doesn't just bulge upwards but creates ripples and waves that move across it; these wave patterns depend on where and how hard you hit it, just like how different forces act on a membrane.
Defining the Membrane's Set-Up
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us consider:
- A rectangular membrane lying in the xy-plane, occupying the domain 0<x<a, 0<y<b.
- It is tightly stretched and fixed along the boundary.
- Let u(x, y,t) represent the vertical displacement of the membrane at position (x,y) and time t.
Detailed Explanation
In this description, we are setting up a rectangular membrane, specifically visualizing it within a coordinate system (the xy-plane). This setup occupies a defined area between two lengths (0<x<a for the x-axis and 0<y<b for the y-axis). The membrane is held taut at its edges, meaning it isn’t able to sag or droop. The vertical displacement of any point on this membrane is represented as u(x, y, t), where 'u' tells us how far a point on the membrane has moved from its original position (the 'rest' state) at any particular time 't'.
Examples & Analogies
Think of a rectangular trampoline. The boundaries are tightly secured to the ground, and when someone jumps on it, the surface moves up and down. The position of any point on the trampoline can be described with coordinates, similar to how we describe points on the membrane.
Assumptions for the Model
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Assumptions:
- The membrane is homogeneous and isotropic.
- Tension T is uniform across the surface.
- The motion is small (linearization valid).
- No external force acts during motion (free vibration).
Detailed Explanation
Several assumptions are made to simplify the analysis of the vibrating membrane. First, saying the membrane is homogeneous means that its material properties (like density and elasticity) are the same everywhere, while isotropic indicates that its behavior is the same in all directions. Uniform tension means that the forces pulling on the membrane are evenly distributed across its surface. The assumption of small motion, or linearization, suggests that we can approximate the curved shapes of vibrations as straight lines when looking at small deviations. Lastly, stating that there are no external forces allows us to solely focus on the behavior of the membrane as it vibrates freely after being disturbed.
Examples & Analogies
Consider a rubber band stretched uniformly in all parts. If you pluck it gently, it vibrates back and forth. The assumptions allow us to treat the rubber band as being the same everywhere (homogeneous) and ensuring that the tension is consistent throughout, which simplifies our study of its vibrations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Vibrating Membrane: A thin and flexible surface that resonates when disturbed.
-
Boundary Conditions: Constraints that define membrane behavior at the edges.
-
Free Vibration: Movement of the membrane without external forces.
-
Homogeneous Materials: Uniform properties throughout the membrane.
-
Isotropic Materials: Identical properties in all directions of the membrane.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A drumhead as a classic example of a vibrating membrane, showcasing distinct sound patterns.
-
A piece of architectural fabric that vibrates under wind pressure, influencing building design.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
A membrane that's stretched real tight, vibrates with all its might!
📖 Fascinating Stories
-
Once a flexible membrane was stretched over a drum, it loved the music that made it hum, but when the winds pressured it, vibrations came alive in a warm dance!
🧠 Other Memory Gems
-
To remember properties of membranes: H for Homogeneous, I for Isotropic, T for Tension.
🎯 Super Acronyms
M.O.V.E
- Membrane
- Oscillation
- Vibration
- External Force (Highlighting key concepts).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Membrane
Definition:
A thin, flexible surface stretched tightly across a frame.
-
Term: Boundary conditions
Definition:
Constraints applied to the edges of the membrane that influence its vibrations.
-
Term: Tension
Definition:
The force applied along the surface of the membrane, influencing its vibration behaviors.
-
Term: Homogeneous
Definition:
Having uniform characteristics across the entire surface.
-
Term: Isotropic
Definition:
Material properties that are identical in all orientations.
-
Term: Free vibration
Definition:
The motion of a membrane without any external forces acting upon it.
-
Term: Linearization
Definition:
The process of approximating a nonlinear problem using linear equations due to small motion.