Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Damping
Unlock Audio Lesson
Today, we're discussing the effects of damping in vibrating systems, specifically how it modifies our equations and influences energy loss. Remember, damping refers to the gradual loss of vibrational energy.
Why is damping important in engineering?
Great question! Damping is essential as it prevents resonance—excessive vibrations that can lead to structural failure. Think of it as a safety buffer.
How does damping actually modify the two-dimensional wave equation?
Damping modifies the wave equation by adding a damping term. The equation is now written as ∂²u/∂t² + 2β∂u/∂t = c²∇²u, where β is the damping coefficient.
So, what does that mean for the solutions of the equation?
It means that the solutions will decay over time, as they are influenced by e^{-βt}, which models the gradual loss of energy. This decay is crucial for ensuring models represent real-world behavior.
Can we see where damping is applied in real structures?
Absolutely! Damping is significant in earthquake-resistant designs and vibration isolators. In these structures, damping systems absorb and dissipate energy from vibrations, protecting the integrity of the design.
To summarize, damping plays a vital role in ensuring stability and safety by mitigating excessive vibrations and energy loss in structures.
Practical Applications of Damping
Unlock Audio Lesson
Let’s dive deeper into how damping is practically applied in engineering. What are some examples anyone can think of?
I've heard about using damping in bridges for earthquake resistance.
Yes! That's a perfect example. By incorporating damping mechanisms in bridges and tall structures, we reduce the risk of resonating frequencies during earthquakes. This proactive measure saves lives and property!
What about in soundproofing?
Exactly! Damping materials are utilized in soundproof membranes to absorb sound energy, preventing noise from traveling through walls or floors. It's very useful in buildings like concert halls or recording studios.
So, damping can enhance comfort too?
Absolutely! Incorporating damping technology can improve the comfort and safety of living spaces, especially in urban environments where vibrations from traffic might be an issue.
In summary, damping really touches a lot of aspects in civil engineering.
Correct! Remember, damping is no small matter; it's a crucial consideration for the safety and longevity of structures. Always think about its application in your designs.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section outlines the modification of the two-dimensional wave equation to account for damping, represented by a damping coefficient. It highlights the significance of damping in reducing resonance risk and its applications in earthquake-resistant design and vibration isolation.
Detailed
Effects of Damping
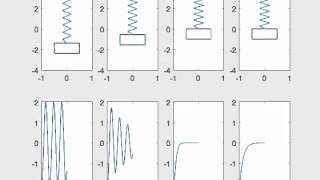
In practical applications, all materials demonstrate damping, which refers to the gradual loss of vibrational energy over time when subjected to oscillations. This phenomenon is crucial to consider in engineering, particularly within the context of the two-dimensional wave equation, where the equation needs to be revised to factor in damping. The modified wave equation is given by:
\[ \frac{\partial^2 u}{\partial t^2} + 2\beta \frac{\partial u}{\partial t} = c^2 \nabla^2 u \]
Here, \( \beta \) represents the damping coefficient that quantifies the rate at which energy is dissipated as the system vibrates. The solutions to this modified equation exhibit decay over time, reflecting an oscillating behavior dampened by the factor \( e^{-\beta t} \).
Engineering Relevance:
- Damping Reduces Resonance Risk: By dissipating energy, damping helps to prevent excessive oscillations that can lead to structural failure.
- Important in Earthquake-Resistant Design: Structures can be designed with damping systems that alleviate the forces exerted during seismic events.
- Applied in Vibration Isolators and Soundproof Membranes: Effective in enhancing comfort and safety in various building designs.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Damping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In practice, all materials exhibit damping, i.e., gradual loss of vibrational energy.
Detailed Explanation
Damping refers to the effect that causes a vibrating system, such as a membrane, to gradually lose energy over time. This energy loss manifests as a decrease in the amplitude of oscillations, which means that the vibrations become less intense and eventually stop. Every real material has some degree of damping, which is critical to consider in engineering applications to predict how structures will behave when subjected to dynamic forces.
Examples & Analogies
Think of damping like a swing in a playground. When you push a swing, it moves back and forth vigorously at first, but eventually, the swing slows down because of air resistance and friction at the pivot. Similarly, materials vibrate initially but lose energy and eventually come to rest due to damping.
Modification of the Wave Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The 2D wave equation is modified as:
∂²u / ∂t² + 2β ∂u / ∂t = c²∇²u
where β is the damping coefficient.
Detailed Explanation
The inclusion of damping in the wave equation introduces a new term. Specifically, the second derivative of displacement with respect to time (∂²u/∂t²) is modified by adding a term that accounts for the damping effects. The value 'β' represents the damping coefficient and determines how quickly the energy is lost from the system. As this coefficient increases, the vibrations cease more quickly.
Examples & Analogies
Imagine a car's suspension system. As the car traverses bumps, the dampers within the shocks help absorb the energy, preventing excessive bouncing. If those dampers are too soft (high damping), the car will settle quickly after hitting a bump, ensuring a smoother ride. In the wave equation, increasing the damping coefficient β translates to quicker energy dissipation in the vibrating structure.
Decay of Solutions Over Time
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Solutions in this case decay over time:
u(x, y,t)=e^{-βt}⋅(oscillating part)
Detailed Explanation
When damping is present, the solution to the wave equation takes a specific form where the amplitude of the oscillation decays exponentially over time. The term 'e^{-βt}' indicates that as time (t) increases, the overall displacement diminishes, leading to lower and lower vibrations until they eventually stop. This behavior is crucial for understanding how structures such as floors and bridges respond to dynamic loads.
Examples & Analogies
Consider a tuning fork that you strike to make it vibrate. Initially, you hear a clear tone, but over time, the sound softens and eventually fades away. This fading is similar to the exponential decay depicted in the solution; as the tuning fork loses energy due to damping, the sound diminishes over time.
Engineering Relevance of Damping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Damping reduces resonance risk.
- Important in earthquake-resistant design.
- Applied in vibration isolators and soundproof membranes.
Detailed Explanation
Damping plays a critical role in engineering applications. By reducing the amplitude of vibrations, it helps prevent resonance, where a structure's natural frequency matches the frequency of external forces, leading to potentially catastrophic failures. In earthquake-resistant designs, proper damping ensures that buildings can withstand seismic forces without excessive oscillations. Similarly, vibration isolators reduce unwanted vibrations in structures and soundproof membranes help manage noise levels.
Examples & Analogies
Think of a well-designed building during an earthquake. Buildings with proper damping features can sway gently and absorb shocks, similar to how a well-built tree sways in the wind without breaking. A tree’s flexibility and resilience help it survive storms just as damping features allow buildings to absorb energy during seismic events.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Damping: The gradual loss of vibrational energy in materials.
-
Damping Coefficient (β): A value representing the amount of damping in a system.
-
Modified Wave Equation: The wave equation adjusted to include damping effects.
-
Decay of Solutions: The gradual reduction in amplitude of oscillations over time due to damping.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of damping is how materials in bridges absorb energy from seismic activity to protect the structure during an earthquake.
-
Another example is the use of vibration isolators in buildings, which help reduce noise and vibrations from external sources.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Damping makes vibrations sway, keeping failures at bay.
📖 Fascinating Stories
-
Imagine a bridge that dances gently in the wind. Thanks to the damping mechanisms, it sways without danger, absorbing the energy like a calm dancer.
🧠 Other Memory Gems
-
Remember: D.A.M.P - Damping Absorbs Mechanical Pressure - to recall the function of damping in engineering.
🎯 Super Acronyms
DAMP
- Damping Absorbs Mechanical Pressure.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Damping Coefficient (β)
Definition:
A parameter that quantifies the rate at which energy is dissipated from a vibrating system.
-
Term: Resonance
Definition:
The condition that occurs when a system's natural frequency matches the frequency of an external force, potentially leading to excessive vibrations.