PID Controllers
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to PID Control
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to discuss a vital concept in robotics called PID control. Can anyone tell me what they think PID stands for?

Is it Proportional, Integral, and Derivative?

Exactly! PID stands for Proportional, Integral, and Derivative. These three components work together to improve the performance of control systems. Let's start with the Proportional component. What do you think it does?

I think it helps in reducing the error, right? By doing something based on the difference between where you are and where you want to be.

That's correct! The Proportional part calculates the error and produces an output that is proportional to this error. Now, who can tell me why we need the Integral part?

Maybe to handle the total accumulation of the error over time?

Right! The Integral component accounts for the accumulated error; it helps eliminate any steady-state error, ensuring the system reaches the desired target. Finally, how does the Derivative part help?

It predicts future errors based on how fast the error is changing?

Yes! The Derivative action helps dampen the system and improve stability by anticipating future trends in the error. Great job, everyone! So, PID controllers combine all these factors to achieve precise control.
Applications of PID Controllers
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's delve into where PID controllers are utilized in robotics. Can anyone mention an application?

I know they're used in motion control, like for robotic arms.

Correct! PID controllers are essential for motion control systems. They help smooth out the movements of robotic arms, ensuring they reach their position accurately. What about other applications?

I think they might be used in temperature regulation in smart systems.

Spot on! PID controllers are widely used in temperature control systems, maintaining desired temperatures by adjusting heating elements based on the detected temperature. Can anyone think of another example?

What about in automated assembly lines? They could help with the movement of conveyor systems?

Absolutely! PID controllers optimize the speed and positioning of conveyor belts, ensuring products are processed efficiently. Excellent responses!
Benefits of PID Control
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's talk about the benefits of using PID controllers in control systems. What do you think is the biggest advantage?

They can be really precise, right?

Exactly! They provide accurate control by continually adjusting based on real-time feedback. What else?

They can work in various applications, making them versatile?

Correct! Their versatility is a significant asset. Besides that, they help in stabilizing systems quickly. Can anyone think of a possible limitation of using PID controllers?

Maybe they can be challenging to tune correctly?

That's right! Tuning PID controllers can be complex, involving finding the right balance of P, I, and D parameters. Overall, the benefits often outweigh the challenges, making them crucial in robotics.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
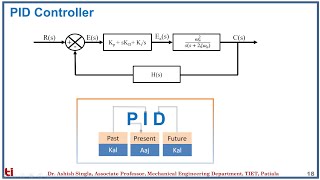
Proportional-Integral-Derivative (PID) controllers are crucial in robotics for providing control mechanisms that adjust output based on error measurements. By responding to the error's magnitude, its cumulative value, and the rate of change, PID controllers significantly enhance motion control and other regulated systems.
Detailed
PID Controllers
PID control is a foundational element in robotics that enhances the precision and efficiency of automatic systems. The Proportional-Integral-Derivative (PID) controller employs three distinct actions:
- Proportional (P): This part of the controller produces an output that is proportional to the current error, which is the difference between a desired setpoint and a measured process variable. It helps reduce the overall error but may not eliminate it entirely.
- Integral (I): This term accounts for the cumulative error over time, addressing any residual steady-state error that the proportional term might leave. It integrates the error with respect to time, thus improving system accuracy.
- Derivative (D): This component predicts the future error based on its rate of change. By responding to how quickly the error is changing, the derivative action helps dampen the system, preventing overshoot and improving stability.
The significance of PID controllers lies in their versatility and effectiveness across various applications, including motion control, temperature regulation, and pressure systems. They are crucial for achieving desired movements in robotic systems, making them a pillar in automation and control theory.
Youtube Videos





![PID Controller - Explained In Hindi [Animation]](https://img.youtube.com/vi/5-iPnjU_q7I/mqdefault.jpg)

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to PID Control
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Proportional-Integral-Derivative (PID) control is widely used in robotics.
Detailed Explanation
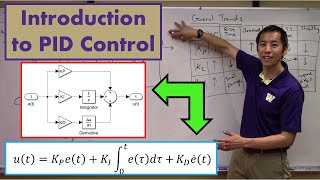
PID control is a widely adopted control strategy in robotics due to its effectiveness in managing how a robot reacts to changes in its environment. The main function of a PID controller is to calculate an error value as the difference between a desired setpoint (what we want the system to achieve) and a measured process variable (what the system is currently achieving).
Examples & Analogies
Imagine driving a car. If you want to go 60 miles per hour, but you are currently going 50 miles per hour, you feel the need to press the accelerator. Here, the speed you desire represents the setpoint, and your current speed is the process variable. The PID controller in this case is like your brain, which determines how much to press the accelerator - how quickly you need to accelerate to reach your target speed without overshooting it.
Components of PID Control
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• It adjusts the output based on error magnitude (P), cumulative error (I), and rate of error change (D).
Detailed Explanation
PID stands for Proportional, Integral, and Derivative, which represent three terms that the controller uses to compute its output. The Proportional (P) term produces an output that is proportional to the current error, meaning that the larger the error, the more correction is applied. The Integral (I) term considers the accumulated past errors, which helps eliminate residual steady-state errors. The Derivative (D) term predicts future errors based on the current rate of error change, which helps dampen the system's response and reduces overshooting.
Examples & Analogies
Think of mixing paint. The Proportional component is like adjusting the amount of a color based on how far off you are from your desired shade. The Integral component is similar to remembering how much color you have previously added, helping you fine-tune to get just the right color. Lastly, the Derivative component is like anticipating how quickly the paint will dry, allowing you to adjust for future changes as you mix.
Applications of PID Controllers
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Crucial in motion control, temperature regulation, and pressure systems.
Detailed Explanation
PID controllers are utilized in various applications where precise control is required. In motion control, for instance, they ensure that a robot arm moves to a specific position with precision. In temperature regulation, a PID controller can maintain a heater's temperature by continuously adjusting the power output based on the temperature difference. Similarly, in pressure systems, PID controllers help maintain desired pressure levels by adjusting valves or pumps accordingly.
Examples & Analogies
Consider a home heating system. A PID controller can manage the temperature by analyzing the difference between the temperature you want (the setpoint) and the actual temperature of your home. If it’s too cold, the system might heat more (Proportional), adjust for how long it has been cold (Integral), and also predict how quickly the temperature will increase (Derivative) for the best response to keep your home comfortable.
Key Concepts
-
PID Control: A control method using proportional, integral, and derivative actions to maintain desired performance.
-
Proportional Action: Output is proportional to the current error.
-
Integral Action: Accounts for accumulated past error to eliminate steady-state bias.
-
Derivative Action: Predicts future errors based on the current rate of change.
Examples & Applications
A robotic arm uses a PID controller to ensure precise movement to a designated position, adjusting as it detects any error from its target.
In temperature control systems, a PID controller continuously adjusts heating elements to maintain the set temperature based on feedback from temperature sensors.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
For PID that’s oh so neat, Proportional makes things meet, Integral keeps bias low, Derivative sets the flow.
Stories
Imagine a robot chef adjusting heat in a frying pan. The Proportional sense if it's too hot or cold, Integral keeps an eye on the overall temperature throughout the cooking, while Derivative ensures the chef reacts quickly to prevent burning.
Memory Tools
Use the acronym 'PID': P for Present settings, I for Increasing past errors, D for Detecting future changes.
Acronyms
'PID' helps you FIND
Follow current error
Integrate past errors
Detect future changes.
Flash Cards
Glossary
- Proportional Control
A control mechanism that outputs a response proportional to the current error.
- Integral Control
A control mechanism that sums past errors to eliminate steady-state error.
- Derivative Control
A control strategy that predicts future errors based on the rate of change of the current error.
- Feedback
The process of using information from the output of a control system to adjust its inputs.
Reference links
Supplementary resources to enhance your learning experience.
