Inverse Kinematics
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Inverse Kinematics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll delve into Inverse Kinematics, or IK. Can anyone explain what it means in the context of robotics?

It's about figuring out the joint angles needed for the robot to reach a specific position.

Exactly! The goal of IK is to achieve a certain end-effector pose, which includes both position and orientation. Can someone tell me what a 'pose' exactly means?

I think it's the robot's specific location and how it's tilted or rotated.

Great explanation! Remember, a pose is critical in making sure the robot performs tasks correctly. Let’s keep that in mind as we discuss the different types of solutions to the IK problem.
Types of Inverse Kinematics Solutions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's break down the types of IK solutions. What are the two main types?

Analytical and numerical solutions!

Correct! Can anyone differentiate between the two?

Analytical solutions give you exact formulas for simple systems, while numerical solutions are more for complex systems that require approximation.

Well put! Analytical solutions work well with simpler robots, like those with 2 to 3 degrees of freedom. Numerical solutions like Newton-Raphson are great for more complicated setups.
Handling Multiple Solutions in IK
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s discuss a fascinating aspect of IK – multiple solutions! Who can provide an example of when this might occur?

Perhaps when a robotic arm has more than one way to configure itself to reach the same end-effector position?

Exactly! A 6-DOF robot can have as many as 16 valid configurations to reach a point. Why do you think it's essential to manage these multiple solutions?

It helps in choosing the most efficient or safest position for the robot to handle tasks without causing collisions.

Very insightful! Remember, redundancy in manipulators means you have to factor in multiple configurations to find the optimal movement.
Constraints in Inverse Kinematics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s now focus on constraints we may encounter in IK. Can anyone name a few?

Joint limits, workspace boundaries, and collision avoidance!

Great! These constraints are crucial for effective IK solutions. Why do you think understanding these limits is vital in civil engineering applications?

Because if we ignore them, the robot could hit something or not be able to reach certain areas safely.

Exactly! Collision avoidance is especially critical in confined environments. Keep these factors in mind as you design and apply IK solutions.
Wrap-Up and Summary of Inverse Kinematics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

As we wrap up, what are the main points we’ve learned about Inverse Kinematics?

IK helps us find joint configurations for desired end-effector poses.

We discussed types of solutions: analytical for simple systems and numerical for complex ones.

We also learned about handling multiple solutions and critical constraints in IK.

Excellent summaries! Remember, mastering these concepts is key to effectively using robots in practical applications. Keep practicing your understanding of IK!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Inverse Kinematics (IK) is essential in robotics for controlling a robot's movements by finding the joint parameters necessary to achieve specific end-effector poses. This section discusses the types of IK solutions, challenges, and constraints associated with solving IK problems.
Detailed
Inverse Kinematics
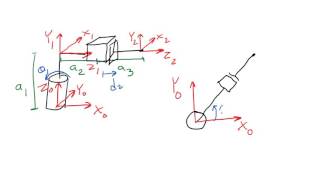
Inverse Kinematics (IK) is a fundamental concept in robotics that involves calculating the joint parameters required for a robotic manipulator to reach a desired position and orientation of its end-effector. The primary goal of IK is to determine the angles (or positions) of the joints that will achieve a specified pose, as represented by a transformation matrix (
T_0n
). The importance of IK can be seen in applications ranging from robotic arms in manufacturing to autonomous systems navigating through complex environments.
Key Concepts:
- The IK Problem: The challenge lies in finding joint angles (
θ_1, θ_2, ..., θ_n
) such that the end-effector reaches the specified pose represented by
Tn = f(θ_1, θ_2, ..., θ_n).
-
Types of Solutions:
- Analytical Solutions: Provide closed-form expressions but are only feasible for simpler manipulators (2-3 Degrees of Freedom).
- Numerical Solutions: Utilize iterative methods (like Newton-Raphson and Gradient Descent) for more complex manipulators with higher DOF.
- Multiple Solutions: An IK problem can have multiple, one, or no solutions. For example, a 6-DOF manipulator can have up to 16 valid configurations.
- Constraints in IK: Practical limitations such as joint limits, workspace boundaries, and collision avoidance must be considered, as well as addressing singularities, where the control becomes unstable.
Understanding IK is essential for the design and implementation of robotic systems, especially in fields like civil engineering, where precise manipulations are necessary.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding the IK Problem
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Given a desired transformation matrix T 0n, find values of θ 1,θ 2,...,θ n (or other joint variables) such that:
Tn = f(θ 0, θ 1, θ 2, ..., θ n)
Detailed Explanation
Inverse Kinematics (IK) involves determining the angles or positions (joint parameters) needed at the joints of a robotic arm to achieve a certain position and orientation of the end-effector. The end-effector is the part of the robot that interacts with the environment, like a hand or tool. The problem can be mathematically represented as finding the joint configuration that fulfills a specific transformation matrix, which encapsulates both the positional and rotational states of the end-effector.
Examples & Analogies
Think of a robotic arm similar to your own arm. If you want to pick up a cup on the table, your brain must calculate how to move your joints (elbows, wrists) to get your hand to the right spot at the correct angle. IK does the same for robots, helping them reach their target position and orientation.
Types of Solutions in IK
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
There are two main types of solutions for IK:
- Analytical Solution:
- Closed-form expressions.
- Possible only for simple manipulators (e.g., 2 or 3 DOF arms).
- Numerical Solution:
- Iterative techniques like Newton-Raphson or Gradient Descent.
- Suitable for complex and redundant manipulators.
Detailed Explanation
IK solutions can be categorized into two types: analytical and numerical. The analytical solution uses direct formulas to compute joint variables. It works well for simpler robotic arms with fewer degrees of freedom (DOF), typically two or three. In contrast, numerical solutions use algorithms to approximate joint positions and are better suited for more complex robots. Numerical methods iteratively adjust joint angles until the desired position is reached, often using techniques like Newton-Raphson or Gradient Descent, which refine guesses based on current error.
Examples & Analogies
Imagine trying to solve a puzzle. If it’s a simple puzzle with a few pieces, you can quickly see how they fit together—that’s like the analytical solution. However, if it’s a complex puzzle with thousands of pieces, you might need to try placing pieces one at a time until the picture comes together—that’s akin to the numerical method.
Multiple Solutions in IK
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
IK may have multiple, one, or no solution. For example, a 6-DOF manipulator can have up to 16 valid configurations. Redundancy (more than 6 DOF) leads to infinite solutions.
Detailed Explanation
In some cases, there can be multiple configurations for the same end-effector position. This phenomenon occurs particularly in more complex robotic systems, where different joint arrangements can still achieve the same goal. For instance, a robot with 6 degrees of freedom might find up to 16 valid ways to position its end-effector in a specific place. If a robot has more than 6 DOF, it can create countless configurations, leading to what we call redundancy, where various positions can achieve the same endpoint.
Examples & Analogies
Think of a person reaching for a cookie on a high shelf. There are many ways to stretch up—standing on tiptoes, using a step stool, or stretching with one arm while standing sideways. Each method might reach the cookie, just like different joint positions can achieve the same end-effector position in a robotic arm.
Constraints in IK Solutions
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Constraints include physical constraints such as joint limits and workspace boundaries, collision avoidance, and singularities where control becomes unstable or impossible.
Detailed Explanation
While solving an IK problem, several constraints must be considered to ensure that the robot can move efficiently and safely. Physical constraints refer to the limits of how far each joint can move, preventing the robot from reaching impossible configurations. Workspace boundaries define the physical space where the robot can operate effectively. Collision avoidance is critical, especially in tight or cluttered environments where the robot must navigate around objects. Singularities represent positions where the robot's control can become erratic, and solutions may not exist.
Examples & Analogies
Imagine trying to walk through a crowded room. You have to avoid bumping into people (collision avoidance), stay within the room's walls (workspace boundaries), and you can only move your legs so far without straining them (physical constraints). In robotics, the same principles apply when considering how a robot moves and operates.
Key Concepts
-
The IK Problem: The challenge lies in finding joint angles (
-
θ_1, θ_2, ..., θ_n
-
) such that the end-effector reaches the specified pose represented by
-
Tn = f(θ_1, θ_2, ..., θ_n).
-
Types of Solutions:
-
Analytical Solutions: Provide closed-form expressions but are only feasible for simpler manipulators (2-3 Degrees of Freedom).
-
Numerical Solutions: Utilize iterative methods (like Newton-Raphson and Gradient Descent) for more complex manipulators with higher DOF.
-
Multiple Solutions: An IK problem can have multiple, one, or no solutions. For example, a 6-DOF manipulator can have up to 16 valid configurations.
-
Constraints in IK: Practical limitations such as joint limits, workspace boundaries, and collision avoidance must be considered, as well as addressing singularities, where the control becomes unstable.
-
Understanding IK is essential for the design and implementation of robotic systems, especially in fields like civil engineering, where precise manipulations are necessary.
Examples & Applications
A robotic arm needing to position a gripper at a specific point while avoiding obstacles around it.
In a production line, a robotic arm equipped with IK to adjust its position to handle different shapes of parts.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In IK, the joints we must pick, to place the end-effector just right. With angles precise, and limits in sight, we solve the pose, making it tight.
Stories
Imagine a robotic arm in a factory, reaching to assemble parts. To do this, it needs to find the right angles to its joints. Just like a person stretching to grab a box from a high shelf, the arm calculates its positions and avoids obstacles, ensuring they don't clash.
Memory Tools
Use the acronym 'IK-SOLVE' to remember: I - Identify desired pose, K - Know joint limits, S - Solve for angles, O - Optimize configuration, L - Look for multiple solutions, V - Verify collision avoidance, E - Execute movement.
Acronyms
IK stands for 'Inverse Kinematics', which is key in robotics for determining joint positions.
Flash Cards
Glossary
- Inverse Kinematics (IK)
The process of determining the joint parameters needed for a robot to achieve a desired end-effector position and orientation.
- Degrees of Freedom (DOF)
The number of independent variables that define the configuration of a robot.
- Analytical Solution
A closed-form solution to the IK problem, usually applicable for simpler robotic configurations.
- Numerical Solution
An iterative approach to solving the IK problem, applicable for complex or redundant robots.
- Redundancy
When a robot has more degrees of freedom than necessary to perform a task, allowing for multiple configurations.
- Constraints
Limitations in the IK process, such as joint limits, collision avoidance, and workspace boundaries.
- Singularity
A configuration where the manipulator loses control or the Jacobian becomes non-invertible.
Reference links
Supplementary resources to enhance your learning experience.
