Enrol to start learning
Reading is open to everyone. Enrolling is free, and it is what unlocks the audio lessons, practice tests and progress tracking.
10.4. Jacobian Matrix in Kinematics
Learn content
Interactive Audio Lesson
Unlock the classroom podcast
The transcript is free to read. A free account plays the conversation back.
Today we’re going to learn about the Jacobian matrix in kinematics! Can anyone tell me what they think a Jacobian matrix does?
Is it related to how joints in a robot move?
Exactly! The Jacobian matrix relates joint velocities to the end-effector velocities. It's like a translator for the robot's movements. We can summarize it with the equation: X˙ = J(q) ⋅ q˙.
What do you mean by end-effector velocity?
Great question! The end-effector is the part of the robot that interacts with the environment, like a hand or a tool. The Jacobian tells us how fast this part moves based on the movements of the joints.
Why is understanding this important?
Understanding the Jacobian is critical for making smooth motions and avoiding issues like singularities, where the robot can lose certain movements. Let’s remember: Jacobian is Joseph’s Velocity Translator!
Unlock the classroom podcast
The transcript is free to read. A free account plays the conversation back.
Now, let’s delve deeper into how the Jacobian matrix connects joint velocities to the end-effector's linear and angular velocities. Who can tell me what these terms mean?
I think linear velocity is how fast it moves in space, and angular velocity is how fast it rotates?
Spot on! The Jacobian matrix allows us to quantify both. When we express this mathematically, we combine these two aspects into the output of the Jacobian. Do you remember the functions we noted earlier?
Yes! X˙ for end-effector velocity and q˙ for joint velocity.
Right! So it helps us understand how movements in the joints result in movements in the end-effector. It's crucial for programming robots to behave predictably!
Unlock the classroom podcast
The transcript is free to read. A free account plays the conversation back.
Let’s talk about singularities next. What do you think happens to the Jacobian at a singularity?
Does it mean that the robot can’t move?
Exactly! At singularities, the Jacobian becomes non-invertible, and certain movements are impossible. This is crucial for robot design to avoid unreachable configurations.
How can we avoid these problems?
By identifying these singularities during the design phase, we can reposition components or adjust the joint configurations to ensure smooth operations. Remember: Singularities are the robot’s hidden traps!
Overview
Short Summary
The Jacobian matrix relates joint velocities to end-effector velocities, playing a critical role in robotic kinematics.
Medium Summary
In kinematics, the Jacobian matrix expresses the relationship between the joint velocities of a robot and the velocity of its end-effector, including both linear and angular components. Understanding the Jacobian is essential for motion control and stability, especially near singularities.
Detailed Summary
Jacobian Matrix in Kinematics
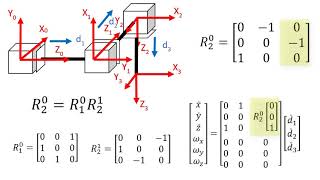
The Jacobian matrix (denoted as J) is a fundamental concept in robot kinematics that serves to relate the velocities of a robot's joints to the resulting linear and angular velocities of its end-effector. Mathematically, this is represented by the equation:
Where:
- X˙ represents the end-effector velocity vector,
- q˙ is the joint velocity vector,
- J(q) is the Jacobian matrix evaluated at the joint configuration q.
Significance of the Jacobian Matrix
The Jacobian matrix is crucial in robotic applications for the following reasons:
- Velocity Transformation: It transforms joint velocities into end-effector velocities, allowing for dynamic control of robotic movements.
- Manipulability Analysis: The Jacobian matrix is used to determine the manipulability of the robot, which assesses its ability to move in various directions.
- Singularities: Understanding the Jacobian helps identify singular configurations, where the matrix becomes non-invertible, causing loss of movement in certain directions. Recognizing and avoiding these singularities is key in the design and control of robotic systems.
Reference YouTube Videos
Audio Book
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountThe Jacobian matrix (J) relates the joint velocities to the end-effector linear and angular velocities.
X˙ = J(q)⋅q˙
Where:
- X˙ is the end-effector velocity vector.
- q˙ is the joint velocity vector.
- J(q) is the Jacobian matrix as a function of joint configuration.
Detailed Explanation
The Jacobian matrix is a mathematical tool used in robotics to relate how the speeds of different joints (the joint velocities) affect the movement of the robot's end effector (the part of the robot that interacts with the environment, like a hand). The equation X˙ = J(q)⋅q˙ shows that the end-effector's velocity is determined by multiplying the Jacobian matrix by the joint velocities. Essentially, if you know how fast each joint is moving (q˙), you can calculate how fast and in which direction the end effector is moving (X˙) using the Jacobian.
Examples & Analogies
Think of a robot arm like your own arm. If you move your elbow and shoulder joint in certain ways, your hand (the end effector) will move in a specific direction. The Jacobian matrix acts like a set of instructions that tells you how fast to move your elbow and shoulder to make sure your hand moves to the desired spot—like reaching for a coffee cup on a table.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountJacobian becomes non-invertible at singularities.
- Robot loses the ability to move in some directions.
- Important to identify and avoid in design and control.
Detailed Explanation
Singularities are special configurations where the Jacobian matrix cannot be inverted, making it impossible to calculate the joint velocities required to achieve a desired end-effector velocity. When a robot reaches a singularity, it may lose the ability to move in certain directions—meaning that even if you want to move the end effector in a specific way, the robot could become stuck or unable to do so. Therefore, it's crucial for designers and engineers to identify these points and design control systems that can avoid them.
Examples & Analogies
Imagine trying to reach for something behind you while standing perfectly straight. You can't turn your body in a complete circle when you’re standing stiffly (that's a kind of singularity). If you bend or twist at the waist or hips, you can reach that object. In robotics, avoiding singularities means making sure the robot can always maneuver to reach its targets, just like bending your body allows you to stretch and grab without getting stuck.
--
Key concepts
Core takeaways and short definitions to help you quickly recall the key ideas from this section.
- Jacobian Matrix:
A mathematical representation that relates joint velocities to end-effector motion.
- End-Effector:
The functional part of a robot that performs tasks.
- Singularity:
A configuration where the Jacobian is non-invertible, leading to movement limitations.
Examples
Step-by-step examples to apply the section's ideas and test your understanding.
A robotic arm's Jacobian matrix can help to compute the required velocities to move the end-effector to a specific point in space.
In surgical robots, understanding the Jacobian allows for precise control over tools and instruments during delicate operations.
Memory aids
Imagine a robot with many joints, each moving to achieve the best points in its path. The Jacobian guides it not to lose its way, ensuring smooth motion every day.
Flash Cards
Glossary
Jacobian Matrix
A matrix that relates joint velocities to end-effector velocities in robotic systems.
End-Effector
The component of a robotic system that interacts with the environment.
Singularity
A condition in which the Jacobian matrix becomes non-invertible, causing loss of movement capabilities.
Joint Velocity
The rate of change of joint parameters with respect to time.
Linear Velocity
The rate of change of position of the end-effector in a straight line.
Angular Velocity
The rate of rotation of the end-effector around an axis.