Pole-Zero Locations in Bode and Laplace Domain Transfer Function
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Transfer Functions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's start by discussing what a transfer function is. It’s a mathematical representation that describes the relationship between the input and output of a system in the Laplace domain.

So, how do we find the transfer function for an RC circuit?

Great question! The transfer function can be found by taking the ratio of the output voltage to the input voltage in the Laplace domain. For an RC circuit, it looks like this: H(s) = V_out(s) / V_in(s) = R / (R + 1/sC).

What does that tell us about the circuit?

It tells us how the voltage output reacts to different frequencies of input signals. The s in our equation represents complex frequency, which we later substitute with jω to analyze the frequency response.

I see! What happens when we substitute s with jω?

Substituting s with jω converts our transfer function into the frequency domain, illustrating how the circuit's gain and phase shift vary with frequency.

Can you summarize what we've learned so far?

Absolutely! We’ve learned that the transfer function is obtained from the Laplace domain and that substituting s with jω allows us to examine the circuit's frequency response.
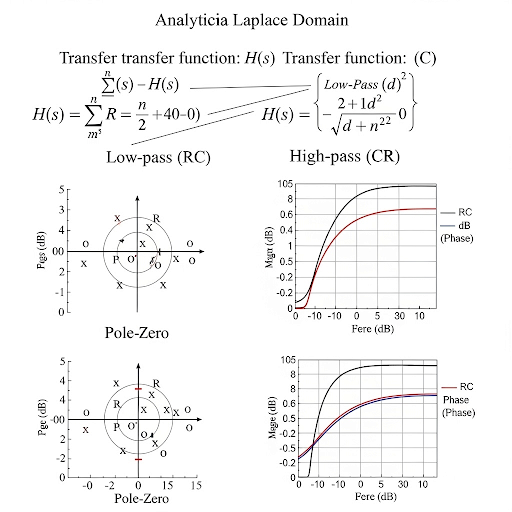
Pole-Zero Locations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let’s discuss the pole-zero plot. Do any of you know why poles and zeros are significant?

I think they help determine how the system behaves at certain frequencies?

Exactly! Poles influence where the frequency response will rise or fall. Each pole in the transfer function corresponds to a specific frequency where the output could tend to infinity.

What about zeros? How do they affect the output?

Zeros can cancel out the effects of poles. When a frequency corresponds to a zero, it causes the output at that frequency to be zero, effectively blocking that frequency from passing through the circuit.

How do we locate the poles and zeros?

We can find them by setting the transfer function's denominator to zero for poles and the numerator to zero for zeros. This gives us valuable insights into the cutoff frequencies and bandwidth of the circuit.

Can you summarize this part for us?

Certainly! We discussed how poles and zeros impact circuit behavior, with poles indicating potential infinite gain points and zeros blocking specific frequencies.
Bode Plots
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's transition to Bode plots, which provide a visual representation of the frequency response. Who can explain what these plots show?

Are they graphs that show gain and phase shift versus frequency?

Absolutely! They represent magnitude in decibels and phase in degrees against a logarithmic frequency scale.

Why do we use a logarithmic scale?

The logarithmic scale allows us to capture a wide range of frequencies and smoothly visualize how the circuit behaves across them.

What’s the significance of the -3 dB point?

The -3 dB point marks the cutoff frequency, indicating where the output is reduced to 70.7% of the maximum output. This provides a measure of bandwidth.

Can you summarize our discussion on Bode plots?

Certainly! We covered how Bode plots illustrate the frequency response of circuits visually, utilizing a logarithmic scale for both frequency and gain.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section covers how the gain of common emitter and common source amplifiers changes with frequency, emphasizing the importance of pole-zero analysis in understanding frequency response. It also introduces concepts such as transfer functions, phase shifts, and Bode plots to illustrate how circuit behavior is influenced by input frequency.
Detailed
Detailed Summary
This section of the chapter focuses on the critical relationship between pole-zero locations in the Laplace domain transfer functions and their implications for the frequency response in analog electronic circuits, particularly common emitter (CE) and common source (CS) amplifiers.
Within the context of circuit analysis, students are guided through the methodologies for determining how changes in input frequency affect the gain of the circuit. Key concepts discussed include the transfer functions derived from both RC and CR circuits, and the transition from the Laplace to the frequency domain.
- Transfer Functions: The section begins with the analytical representation of circuits in the Laplace domain, establishing how to derive transfer functions for RC and CR circuits, leading to insights into their frequency response.
- Pole-Zero Analysis: Emphasis is placed on how the location of poles and zeros in the transfer function directly relates to the circuit's response to various frequencies. For instance, poles signify points where the system's response can potentially become unbounded (infinite gain), while zeros are points that effectively
Youtube Videos

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Transfer Functions in Laplace Domain
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In the Laplace domain, the transfer function of a circuit can be represented as a ratio of polynomial expressions. For the C-R circuit, this is given by:
$$ V(s) = \frac{sCR}{1+sCR} $$
Here, the numerator and the denominator represent the relationship between the input and output voltages in terms of complex frequency s.
Detailed Explanation
A transfer function describes how the input to a system is related to the output, using complex frequency s, which consists of a real part and an imaginary part. In the case of our C-R circuit, the transfer function reflects how the output voltage changes depending on the frequency of the input signal. The function is expressed as a fraction, where the numerator indicates the reactive behavior (due to the capacitor), and the denominator indicates how the circuit as a whole responds to that frequency input.
Examples & Analogies
Think of a transfer function like a recipe for making a cake, where the input ingredients (the voltage or signal applied) are transformed into a final product (the output voltage). In this analogy, the different components of the transfer function (numerator and denominator) dictate how well the ingredients mingle and combine to create the cake, which reflects how the input signal transforms within the circuit.
Frequency Response Transformation
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
To transform from the Laplace domain to the frequency domain, we substitute s with jω, simplifying the transfer function. This gives us the frequency response, showing how the system behaves with different frequencies.
$$ V(jω) = \frac{jωCR}{1+jωCR} $$
Detailed Explanation
Transforming the function by substituting s with jω (the imaginary unit multiplied by the angular frequency) allows us to analyze how the circuit responds specifically to sinusoidal signals at various frequencies. The resulting expression indicates how both the magnitude and phase of the output voltage vary with frequency, directly supporting the analysis of the circuit's performance via frequency response.
Examples & Analogies
Imagine tuning a radio to different stations; each station represents a different frequency. Just like the varying signal from each station can be understood in terms of volume (magnitude) and tone (phase), the transfer function also provides insight into how well our circuit can process these signals at different frequencies.
Magnitude and Phase Response
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The response of the circuit can generally be expressed in terms of both magnitude and phase.
As the frequency varies, the output may shift in amplitude and also undergo a phase shift, which we can represent with the equations derived from the transfer function.
Detailed Explanation
Magnitude response indicates how much power the output signal has compared to the input, while phase response shows how the timing of the output changes concerning the input signal. Typically, at low frequencies, the phase might be close to 90 degrees, indicating a significant delay. As frequency increases, the phase can approach 0 degrees, meaning that the output closely follows the input in time. Understanding both aspects is critical for applications where timing and signal strength are essential, such as in audio amplification systems.
Examples & Analogies
Consider a conductor leading an orchestra. The conductor ensures all musicians play at the right volume (magnitude) and at the right tempo (phase). Just as the orchestra's overall sound changes with the tempo, the circuit's output also varies with frequency, highlighting the importance of tuning both amplitude and timing for a harmonious performance.
Bode Plot: A Practical Representation
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Bode plots are a graphical representation of the frequency response, typically plotted with frequency on a logarithmic scale on the x-axis and the gain in decibels (dB) on the y-axis. The reasoning behind this is to visually present a wide range of frequencies clearly and concisely.
Detailed Explanation
Bode plots provide a clear, visual insight into how gain and phase shift change over frequency. By using a logarithmic scale for frequency, we can represent a broad spectrum (from very low to very high frequencies) in a compact form. The gain is expressed in decibels, a logarithmic measure that makes it easier to interpret relative changes in signal strength, especially in engineering contexts where gain values can vary widely.
Examples & Analogies
Think of a Bode plot like a mountainous landscape where each peak and valley represents different frequencies and their corresponding signal strengths. Just as we might use a map with a logarithmic scale to navigate this terrain easily, engineers use Bode plots to navigate the complex behavior of circuits across varying frequencies, making decisions about design and implementation much clearer.
Key Concepts
-
Transfer Function: Mathematical relationship between input and output in a system, analyzed in the Laplace domain.
-
Pole-Zero Analysis: Useful for determining the behavior of a system around certain frequencies.
-
Frequency Response: Describes how the output of a system varies with frequency input.
-
Bode Plots: Visual representation of gain and phase shift against frequency in a logarithmic scale.
Examples & Applications
Example of finding a transfer function for an RC circuit: H(s) = R / (R + 1/sC), then substituting s with jω.
Example of pinpointing poles and zeros from H(s) = R/(R + 1/sC), leading us to s = -1/(RC) as poles.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When the pole's on the line, the gain's infinite in time.
Stories
Imagine a bridge (the circuit) where cars (signals) must slow down (gain drops) when they hit a bump (a pole), but cannot pass through when the road is blocked (a zero).
Memory Tools
Remember 'P-Z' (P for Pole and Z for Zero) to identify their roles in frequency impact: Poles amplify, and Zeros block.
Acronyms
PZ
Poles yield infinite gains
Zeros lead to zero output.
Flash Cards
Glossary
- Transfer Function
A mathematical representation in the Laplace domain showing the relationship between input and output of a system.
- Pole
A value in the denominator of the transfer function where the function tends to infinity, indicating a frequency where gain could be significant.
- Zero
A value in the numerator of the transfer function where the function equals zero, blocking specific frequencies.
- Bode Plot
A graphical representation of the frequency response of a system showing gain in decibels and phase shift in degrees on a logarithmic scale.
- Cutoff Frequency
The frequency at which the output power drops to half its maximum, corresponding to -3 dB in a Bode plot.
Reference links
Supplementary resources to enhance your learning experience.
