Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Classical Damping
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's start by discussing classical damping. In MDOF systems, classical damping is represented by a matrix that combines mass and stiffness. Can anyone tell me how we express the damping matrix?
Is it like… C equals alpha times M plus beta times K?
Exactly! That's right. Where α and β are constants. This formulation helps simplify our equations while ensuring we can still achieve modal decoupling. Why is this important?
Wouldn't it make solving the equations easier?
Correct! It allows us to analyze dynamic behavior more effectively. Remember the acronym 'CAB'—Classical damping means Algebraic convenience and Behavioral accuracy.
So, using classical damping helps in retaining the essential behavior of structures?
Yes, precisely! Great question! Let's summarize: classical damping simplifies the analysis while maintaining the system's behavior for MDOF systems.
Non-Classical Damping
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s move on to non-classical damping. Non-classical damping often complicates the analysis. What do you think happens with the modal decoupling in these cases?
Isn't it disrupted? We can't easily separate the modes as we do with classical damping?
Exactly! Non-classical damping disrupts modal decoupling, making it challenging—we need advanced numerical techniques or state-space methods. Can anyone think of scenarios where non-classical damping might occur?
Maybe in irregular or composite materials, where the properties change?
Right! That's a great point. Non-classical damping is common in real-world applications, requiring engineers to understand these complexities. Let's recap: non-classical damping complicates analysis, necessitating advanced approaches.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section elaborates on damped MDOF systems, emphasizing the significance of damping in structural analysis. It discusses classical damping, expressed through proportional relationships, and introduces non-classical damping, where modal decoupling becomes complex, necessitating advanced numerical techniques.
Detailed
Damped MDOF Systems
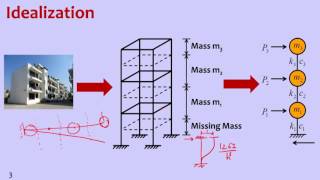
Damped Multi-Degree-of-Freedom (MDOF) systems are crucial for accurately modeling the dynamic response of structures under various loading conditions. Unlike undamped systems, where the equations of motion can be solved easily, damped systems introduce additional complexities due to energy dissipation processes occurring in materials.
16.6.1 Classical (Proportional) Damping
In classical damping, the damping matrix is expressed as a linear combination of mass and stiffness matrices:
$$[C] = \alpha[M] + \beta[K]$$
Here, \(α\) and \(β\) are constants that reflect the contributions from both inertial and stiffness effects, allowing for easier mathematical treatment while preserving the essential features of the system's dynamic behavior.
16.6.2 Non-Classical Damping
However, in many real-world scenarios, damping is non-classical. Non-classical damping complicates the analysis since it interrupts the modal decoupling principle used in classical damping. Engineers must often resort to advanced numerical techniques or state-space methods to address these challenges effectively.
Understanding the characteristics of both classical and non-classical damping is vital for engineers engaged in designing structures that can withstand dynamic loads, particularly in earthquake-prone areas.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Classical (Proportional) Damping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Proportional damping assumes:
[C]=α[M]+β[K]
Where α and β are constants. This assumption ensures that modal decoupling is still valid and results in classical damping.
Detailed Explanation
Classical damping is a simplified model used in engineering to describe how energy is dissipated in oscillating systems, such as buildings during an earthquake. In this model, the damping matrix [C] is expressed as a combination of the mass matrix [M] and the stiffness matrix [K]. The constants α and β play a crucial role; they determine how much damping is associated with the mass and stiffness of the system respectively. This proportionality ensures that the modes of the system can still be analyzed separately, simplifying the calculation.
Examples & Analogies
Think of a swinging pendulum. If you push it, it swings up and down. The air resistance it encounters acts like damping, slowing its motion down. Classical damping is like saying the more a pendulum weighs (mass) and the tougher the materials are that it bounces off from (stiffness), the more controlled its swings would be, allowing engineers to predict its motion more easily.
Non-Classical Damping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In reality, damping is often non-classical, where modal decoupling is not possible. Advanced numerical techniques or state-space methods are required in such cases.
Detailed Explanation
In contrast to classical damping, non-classical damping occurs when the relationship between mass and stiffness does not follow a simple proportionality. This complexity means that the modes of vibration cannot be easily separated, making it difficult to analyze the system's behavior. Engineers have to rely on advanced numerical methods and state-space techniques to compute the structural response under dynamic loading accurately. These methods take into account the complexities of real-world materials and structures, providing more precise predictions in critical situations.
Examples & Analogies
Imagine a car driving over a rough, bumpy road. The way the car absorbs shocks from the bumps is similar to non-classical damping. Unlike straightforward smoothing of oscillations (like classical damping), the shocks from various bumps interact in complex ways. To ensure a smooth ride, car manufacturers use sophisticated suspension systems with advanced technology. Similarly, non-classical damping reflects the complexity of real-life scenarios, requiring engineers to employ advanced tools to understand and predict how structures will respond.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Damped MDOF Systems: Systems where damping is considered for realistic dynamic analysis.
-
Classical Damping: A linear combination of mass and stiffness matrices for damping representation.
-
Non-Classical Damping: Damping that complicates analysis and requires advanced methods.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An engineering analysis of a 10-story building under seismic loading could involve both classical and non-classical damping scenarios.
-
Testing the dynamic response of a composite material bridge, where non-classical damping effects are more prominent.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In systems where forces abound, non-classical damping can turn you around.
📖 Fascinating Stories
-
Imagine a bridge that sways in the wind. It has both mass and stiffness to contend, yet when non-linear forces come into play, it twists and turns in a confusing way.
🧠 Other Memory Gems
-
For damping, think 'Proportional is easy, Non-classical is tough'. 'P-easy, N-tough' reminds us!
🎯 Super Acronyms
Remember 'CANDY' - Classical And Non-Classical Damping Yields behavior understanding.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Classical Damping
Definition:
Damping characterized by a proportional relationship between mass and stiffness matrices, allowing modal decoupling.
-
Term: NonClassical Damping
Definition:
Damping that complicates modal analysis and does not allow for simple decoupling of modes, requiring advanced numerical techniques.
-
Term: Modal Decoupling
Definition:
The process of simplifying a coupled MDOF system into uncoupled SDOF systems for easier analysis.
-
Term: Damping Matrix
Definition:
A matrix representing the damping characteristics in a dynamic system, critical for MDOF analysis.