Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Modal Analysis
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we're going to explore modal analysis, a vital aspect in understanding how complex structures respond to dynamic loads. Why do you think it's important to simplify MDOF systems?
I think it helps us analyze them more easily and determine how they will behave during events like earthquakes.
Yeah, but how exactly does that simplification work?
Great question! We basically transform the coupled equations of motion into uncoupled equations by using a modal matrix. Each mode acts like an independent SDOF system, making calculations manageable.
And does this mean each mode shape contributes separately to the overall response?
Exactly! By employing modal analysis, we can calculate the total response by using modal superposition.
Can you explain what modal superposition means?
Sure! It allows us to combine the effects of each mode's response. So we sum the contributions of all modes to get the overall dynamic response of the structure.
In summary, modal analysis simplifies complex MDOF systems into manageable components, aiding our understanding of structural responses under dynamic loading.
Understanding the Equation of Total Response
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
"Now, let’s discuss the actual process of modal superposition. The equation we use is:
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In modal analysis, MDOF structures are transformed into SDOF systems using a modal matrix, whereby the total response can be found through modal superposition. This method enables each mode to be analyzed independently, facilitating a more manageable approach to understanding and calculating structural responses under dynamic loading.
Detailed
Detailed Summary
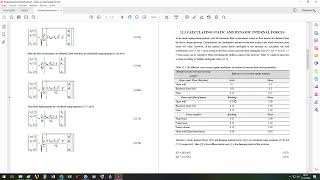
Modal Analysis is a crucial technique for evaluating Multi-Degree-of-Freedom (MDOF) systems, particularly under dynamic loading scenarios like earthquakes. This process involves the transformation of a coupled MDOF system into a set of uncoupled Single-Degree-of-Freedom (SDOF) systems, allowing for the simplification of complex equations of motion. The transformation uses the modal matrix [Φ], enabling each mode of the structure to be treated independently. This independence is significant because it allows for the total response of the dynamic system to be synthesized through modal superposition, leading to the equation:
$$
{u(t)}=∑_{i=1}^{n} {ϕ_i}q_i(t)
$$
Here, {ϕ_i} represents the mode shapes and q_i(t) indicates the generalized coordinates or modal responses associated with each mode. This approach highlights the importance of understanding individual mode behavior in response to dynamic forces, ultimately aiding in the design and safety evaluations of structures subjected to lateral loads.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Modal Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Modal analysis transforms the coupled MDOF system into uncoupled SDOF systems using the modal matrix [Φ]:
Detailed Explanation
At its core, modal analysis is a technique used to simplify complex systems. In this case, we are taking a multi-degree-of-freedom (MDOF) system—which has many interconnected parts responding together—and we break it down into simpler, single-degree-of-freedom (SDOF) systems. Each of these systems can be analyzed independently. This transformation uses a modal matrix denoted as [Φ], which contains the mode shapes of the system. By making this transformation, we can analyze each mode's behavior separately, which simplifies the overall analysis.
Examples & Analogies
Think of a large choir performing a song. If you want to understand how each part (soprano, alto, tenor, bass) contributes to the overall performance, you could isolate each section and listen to them individually. This is similar to modal analysis, where we isolate each mode of the system to understand its behavior better.
Understanding Modal Superposition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
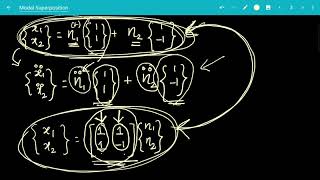
Each mode behaves like a separate SDOF system, and the total response is obtained using modal superposition:
{u(t)}=∑ϕ_i q_i(t)
Where:
- {ϕ_i}: Mode shape of the i-th mode
- q_i(t): Generalized coordinate (modal response)
Detailed Explanation
Once we have transformed our system using modal analysis, each mode can be treated as an independent system. The total response of the original MDOF system is then calculated by summing the contributions from each individual mode, which is what we call modal superposition. The equation shows this process: we take each mode's shape ({ϕ_i}) and its corresponding response ({q_i(t)}) and sum them up. This allows us to effectively compute how the entire system reacts to dynamic loads by combining the behaviors of these simpler modes.
Examples & Analogies
Imagine putting together a jigsaw puzzle. Each piece (mode shape) contributes to the overall picture (total response). To see the full image, you have to connect all the pieces together. Similarly, in modal superposition, by adding up the independent responses from each mode, we recreate the complex response of the entire system.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
MDOF Systems: Structures with multiple degrees of freedom.
-
Modal Analysis: Transforms MDOF systems into simpler SDOF systems.
-
Total Response: The overall dynamic behavior of a structure derived from individual mode responses via modal superposition.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a 10-story building analyzed using modal analysis, the dynamic responses of each floor are modeled individually based on their respective mode shapes and frequencies.
-
A bridge subjected to wind forces is simplified using modal analysis to determine how different spans will twist and sway under load.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In modal analysis, don't you fret, just sum the modes, and no need to sweat.
📖 Fascinating Stories
-
Imagine building a bridge where each section sways independently during a storm. Modal analysis helps predict how each part will react, making the design safer.
🧠 Other Memory Gems
-
To remember the process: Modes Are Sum of Responses—MASR!
🎯 Super Acronyms
For the total response equation, remember SUM
- S: - Shape
- U: - Uncoupled
- M: - Modal contribution.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Modal Analysis
Definition:
A technique that transforms a coupled MDOF system into uncoupled SDOF systems for easier dynamic analysis.
-
Term: Modal Superposition
Definition:
A method of combining the responses of individual modes to derive the overall response of a structure.
-
Term: Modal Matrix [Φ]
Definition:
A matrix that contains the mode shapes of the structure, facilitating the transformation in modal analysis.
-
Term: Degree of Freedom (DOF)
Definition:
An independent displacement or rotation needed to define the motion of a system.