Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Degrees of Freedom
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome, everyone! Today, we are diving into the concept of Degrees of Freedom, or DOF, in structural systems. Can anyone explain what they think a degree of freedom represents?
I think it’s about how something can move, like how far it can go in different directions?
That's a great start! A degree of freedom specifically refers to the independent displacements or rotations needed to define a structure's configuration. In MDOF systems, every floor of a building usually represents one translational DOF. Remember: **D.O.F = Degrees of Flexibility!**
So, does that mean more floors mean more degrees of freedom?
Exactly! For instance, a building with **n floors** typically has **n translational DOFs** in planar settings. Each floor can move independently!
What about frame structures? Do they have different DOFs?
Good question! In frame structures, we might also consider rotational DOFs, further complicating our analysis but allowing for a more accurate representation of the structure’s behavior under load.
So, understanding DOF is really important for engineers designing buildings?
Absolutely! Especially in earthquake engineering, where we need to analyze how structures respond to dynamic forces. Let’s summarize: Each floor counts as one translational DOF, and these concepts help us in accurate modeling of structure motion.
Role of DOF in Earthquake Engineering
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Switching gears, let’s discuss why DOF is particularly vital in **Earthquake Engineering**. Can someone provide a real-world example of its application?
Maybe how buildings are designed to handle shaking during a quake?
Exactly! By modeling the structure with MDOF systems, we capture how each floor might respond to ground motion. This ensures that we can manage the stress and potential failure points in the design.
Do engineers use software to model all these DOFs?
Yes! Advanced software uses these DOF models to conduct simulations and predict how buildings will respond. Remember, knowledge of DOFs leads to more resilient structures!
What happens if we ignore certain DOFs?
Ignoring DOFs can lead to unsafe designs. Structures might not withstand expected forces, particularly during seismic events. Always consider all possible movements!
So, is it safe to say that understanding DOF is crucial for building safety?
Absolutely! By recognizing how each component of a structure interacts, we can design for safety effectively. Remember: **Every Floor Has a Role!**
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Degrees of freedom are crucial in MDOF systems, as each floor of a building typically represents one translational DOF, while others may include rotational ones. The section emphasizes that a structure's motion requires considering all independent displacements and rotations, essential for accurate dynamic analysis, especially in earthquake engineering.
Detailed
Detailed Summary
In structural systems, the concept of Degrees of Freedom (DOF) is fundamental in defining how structures respond to dynamic loads. A degree of freedom represents an independent displacement or rotation necessary to fully define a structure's configuration. In the context of Multi-Degree-of-Freedom (MDOF) systems:
- Each floor of a building can be represented as one translational DOF, allowing the floor to move independently under dynamic loading.
- For frame structures, additional rotational DOFs may also be taken into account, reflecting the movement of structural frames due to forces acting upon them.
- Therefore, a building with n floors generally has n translational DOFs in planar analysis.
Understanding DOF is vital for engineers, particularly in fields such as Earthquake Engineering, where accurately modeling the structure's motion is essential for safeguarding against seismic events.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
What is a Degree of Freedom?
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
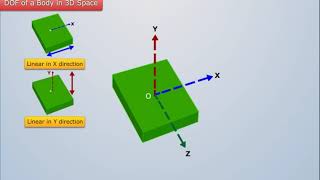
A degree of freedom (DOF) is the number of independent displacements or rotations needed to define the configuration of a structure.
Detailed Explanation
A degree of freedom (DOF) is a key concept in structural analysis. It refers to the number of independent ways a structure can move or rotate. For example, if a structure can move up and down, as well as rotate, it has at least two degrees of freedom. In simple terms, every way in which a structure can move independently counts as a degree of freedom.
Examples & Analogies
Think of a puppet controlled by strings. If the puppet's arms can move independently from its legs, then those movements represent different degrees of freedom. The more strings the puppeteer uses to control the puppet, the greater the range of movements and the complexity of the puppet's motion.
DOFs in MDOF Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In MDOF systems: Each floor of a building typically represents one DOF in a lumped mass model (translational motion). In frame structures, rotational DOFs may also be considered. A structure with n floors would typically have n translational degrees of freedom in planar analysis.
Detailed Explanation
In multi-degree-of-freedom (MDOF) systems like buildings, each floor is treated as if it can move independently. This means that if a building has 'n' floors, it typically has 'n' degrees of freedom, with each floor representing one DOF due to vertical displacement. Additionally, in structures like frames, we can also consider rotational degrees of freedom, which accounts for the turning ability of structural elements. Therefore, the analysis of these systems becomes more complex because we must account for the movements of all these independent components.
Examples & Analogies
Imagine a stack of blocks where each block can slide back and forth. If there are three blocks, each has its own ability to shift independently, resulting in three degrees of freedom. If we also allow each block to tilt or rotate, then we would need to count those rotations too, which adds even more dimensions to how the entire stack can move.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Degrees of Freedom (DOF): Represents independent motions needed to define a structure's configuration.
-
Translational DOF: Each floor in a building typically represents one translational degree of freedom.
-
Rotational DOF: Additional rotational degrees may be considered in frame structures.
-
MDOF Systems: Systems that capture the complexity of real-world structures with multiple independent motions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A ten-story building may be modeled as having ten translational degrees of freedom, one for each floor.
-
A simple frame structure may include both translational and rotational degrees of freedom, allowing for more accurate modeling of how it responds to lateral forces.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Degrees that free make structures sway, one for each floor in a multi-story way.
📖 Fascinating Stories
-
Imagine a building dancing during an earthquake. Each floor has its own moves, representing degrees of freedom. Some floors twist, others just sway - that's how they dodge the shaking ground!
🧠 Other Memory Gems
-
Do Factors Of flexibility (D.F.O.): Remember, each floor's a factor of its own movement!
🎯 Super Acronyms
FLOORS
- Flexibility Leads to Optimal Response Strategies.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Degree of Freedom (DOF)
Definition:
The number of independent displacements or rotations needed to define the configuration of a structure.
-
Term: MultiDegreeofFreedom (MDOF) Systems
Definition:
Systems that represent structures with more than one coordinate (degree of freedom) required to define their motion.
-
Term: Translational Motion
Definition:
Movement along a straight path or direction within a plane.
-
Term: Rotational Degree of Freedom
Definition:
The independent rotation that a structural element can execute in response to applied forces.