Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Mass Distribution in MDOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we'll discuss the importance of mass distribution in MDOF systems. Why do you think it's essential to model mass accurately?
Isn't it because it affects how the structure responds to forces?
Exactly! The mass distribution dictates the dynamic behavior. Remember, if you misestimate mass, you might overestimate or underestimate responses during events like earthquakes. This could lead to catastrophic failures.
So, we need to consider both structural and non-structural elements, right?
Yes! Non-structural elements can include anything from furniture to partitions. Together, they contribute to the overall mass and should be included in the model.
Can we use simplified methods to estimate mass distribution?
While simplifications may help, they can sometimes lead to inaccuracies. Use as much available data as you can. Let's keep that in mind!
To summarize this session, accurate mass distribution is critical for predicting how structures respond dynamically; consider all components in your calculations.
Stiffness Estimation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, we’ll talk about stiffness estimation. How can we estimate the stiffness of a structure?
We can use member properties or finite element stiffness matrices.
Correct! These methods help us model how resistant the structure is to deformation. Would you say that using member properties gives a more accurate picture?
It should, right? Because it directly considers the materials used.
That's right! Accurate stiffness estimation is vital, as it impacts the natural frequencies and mode shapes of the structure—key factors in dynamic analysis.
Does the stiffness have any relation to the boundary conditions we use?
Absolutely! The constraints you impose will change the effective stiffness of the system. This leads us to our next topic on boundary conditions. Remember, stiffness and boundary conditions are interconnected.
In summary, estimating stiffness accurately from member properties enhances understanding of structural behavior, and boundary conditions profoundly affect these estimates.
Boundary Conditions in Structural Modeling
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s focus on boundary conditions and their critical role. Why are boundary conditions so important?
They define how the structure interacts with its supports, right?
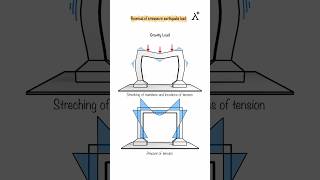
Exactly! Whether the base is fixed, supported, or allowed to move—each scenario will impact the structural response under loading, especially in seismic analysis.
Wouldn't neglecting them lead to unrealistic behavior in our models?
Yes! For example, not considering soil-structure interaction might overlook significant effects on vibrations. Keeping this in mind during modeling is crucial.
How do we ensure that we model them effectively?
You will need to carefully analyze the structure's real-world constraints. Use available ground tests and understand site conditions—it’s critical!
To wrap things up, accurately modeling boundary conditions is essential for realistic responses in MDOF systems; they directly influence vibrations and the global behavior of structures.
Estimating Damping
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Finally, let’s discuss damping estimation. How do we usually estimate damping in MDOF systems?
Often from experimental data or by using empirical assumptions.
Correct! Choosing an accurate damping value is essential as it affects how energy is dissipated during dynamic loading.
What type of damping do we typically consider in these models?
We often assume classical, proportional damping, but keep in mind that real-world systems may behave differently and exhibit non-classical damping.
What happens if we ignore damping?
Ignoring damping can significantly result in exaggerated responses in seismic simulations, which may lead to unsafe design outcomes. Always incorporate realistic damping values.
In summary, effective damping estimation is crucial for capturing energy dissipation in structural responses. Therefore, it impacts the accuracy of seismic analysis in MDOF systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Effective structural modeling involves careful attention to mass distribution, accurate stiffness estimation, the proper application of boundary conditions, and reliable damping estimation. Each of these elements contributes to the overall fidelity of dynamic analyses in MDOF systems, particularly important in the context of earthquake engineering.
Detailed
Practical Aspects in Structural Modeling
In structural modeling for Multi-Degree-of-Freedom (MDOF) systems, accuracy is paramount due to the intricate responses of structures to dynamic loading, such as seismic events. Key practical aspects outlined include:
- Mass Distribution: It's essential to model the mass distribution accurately, accounting for both structural and non-structural elements. This ensures that the dynamic properties of the model closely resemble the real structure's behavior.
- Stiffness Estimation: Proper stiffness estimation is crucial and can be derived from material properties or stiffness matrices from finite element analysis. Accurate stiffness ensures that the model responds realistically to loads.
- Boundary Conditions: Accurate modeling of boundary conditions is vital to replicate realistic interactions between the structure and its supports. For instance, understanding whether a foundation is fixed or experiences soil-structure interaction can significantly impact the dynamics.
- Damping Estimation: Typically sourced from experimental data or empirical assumptions, damping estimation is critical. The correct representation of damping behaviors influences the energy dissipation characteristics during dynamic loading, especially in seismic scenarios.
Together, these aspects form the foundation for effective MDOF system modeling, which is essential in earthquake engineering and other applications requiring precise dynamic response analyses.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Mass Distribution in Structural Modeling
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Mass distribution: Accurate mass modeling (including non-structural elements) is essential.
Detailed Explanation
Accurate mass modeling means that all parts of the structure, including walls, furniture, and any machinery, need to be represented properly in the model. If the mass distribution isn't accurate, the response of the building during an event like an earthquake will be incorrectly predicted, potentially leading to unsafe designs.
Examples & Analogies
Think of a seesaw. If one side has a heavy weight and the other side has a light weight, the balance is off. Similarly, if a building’s mass isn’t balanced properly in the model, it will behave unpredictably during dynamic events.
Stiffness Estimation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Stiffness estimation: May be obtained from member properties or stiffness matrices of finite elements.
Detailed Explanation
Stiffness in a structure relates to how much it resists deformation under load. Engineers estimate stiffness based on the material properties (like Young's modulus) and the geometry of structural members (like beams and columns). Accurate stiffness estimation is crucial, as it directly influences how the structure deforms under loads.
Examples & Analogies
Imagine a thick rubber band compared to a thin one. The thick rubber band is stiffer and will not stretch as much as the thin one under the same load. In buildings, using the correct 'stiffness' of materials helps predict how the building will bend or sway in wind or during earthquakes.
Boundary Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Boundary conditions: Proper constraints must be modeled (e.g., fixed base, soil-structure interaction).
Detailed Explanation
Boundary conditions define how a structure interacts with its supports and the ground. For example, a fixed base means that the structure cannot move at the foundation, which can change how loads are distributed. Soil-structure interaction refers to how the soil beneath affects the building’s response to loads, which needs to be accounted for to ensure accuracy.
Examples & Analogies
Consider a candle placed on a table versus one placed on a pile of pillows. The table provides a stable base, while the pillows might shift under weight, affecting how the candle stands. Similarly, boundary conditions can greatly affect structural performance.
Damping Estimation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Damping estimation: Usually obtained from experimental data or empirical assumptions.
Detailed Explanation
Damping is the mechanism that dissipates energy in a structure, helping to reduce vibrations. Estimating damping is important for dynamic analysis, often derived from experimental data or approximations based on similar structures. Adequate damping helps structures return to their original state after deformation.
Examples & Analogies
Think of how a car’s shock absorbers work. They help dampen the vibrations when driving over bumps, providing a smoother ride. In buildings, damping helps counteract movements caused by winds or earthquakes, ensuring the structure remains stable.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Distribution: Refers to accurately representing the mass in a structure, including non-structural elements.
-
Stiffness Estimation: Involves determining the resistance of a structure to deformation based on its properties.
-
Boundary Conditions: Constraints that affect how a structure interacts with its supports.
-
Damping Estimation: Refers to understanding how a structure dissipates energy during dynamic loading.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A building's mass distribution must consider not only its floors but also furniture, partitions, and mechanical systems for accurate modeling.
-
Proper stiffness estimation can involve using a finite element analysis of a beam to derive its effective stiffness before integrating it into the overall structural model.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For mass, don't be a clown, account for all around!
📖 Fascinating Stories
-
Imagine building a LEGO tower. If you don’t account for the weight of every added piece, it might collapse during play—just like mass in a real structure!
🧠 Other Memory Gems
-
Use 'M-S-B-D' to remember: Mass, Stiffness, Boundary conditions, Damping.
🎯 Super Acronyms
M-S-B-D
- Where M is for Mass
- S: for Stiffness
- B: for Boundary conditions
- and D for Damping.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Distribution
Definition:
The arrangement and allocation of mass throughout a structure, critical for dynamic response considerations.
-
Term: Stiffness Estimation
Definition:
Determining the resistance of a structure to deformation, derived from material properties or finite element models.
-
Term: Boundary Conditions
Definition:
Constraints applied to a structural model that define its interaction with supports and surroundings.
-
Term: Damping Estimation
Definition:
The process of determining the amount of energy dissipation in a structure, typically sourced from experimental data.