Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding MDOF Models
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome everyone! Today we are introducing Multi-Degree-of-Freedom, or MDOF, systems. Why do you think MDOF is important in seismic analysis?
I guess because buildings have many parts that move differently during an earthquake?
Exactly! MDOF systems consider all those interconnecting components. This is crucial during events like earthquakes where each component may respond differently. Can anyone tell me what a Single-Degree-of-Freedom model might miss in this context?
It probably oversimplifies the structure, right?
Correct! SDOF models only look at one motion, ignoring how individual parts can interact. MDOF systems help us capture this complexity.
Importance of Realistic Dynamic Analysis
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's build on what we've discussed. Why do we need accurate analyses in structures during events like earthquakes?
To prevent failures and ensure safety?
Absolutely! An accurate analysis helps engineers design buildings that can withstand seismic forces. How do MDOF systems help us achieve these accurate analyses?
By giving us a better understanding of each part's motion?
Exactly! MDOF systems allow us to simulate how each component moves independently while being connected to others.
Overview of MDOF System Characteristics
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we've discussed the fundamental importance of MDOF systems, let's look at their characteristics. What do you think characterizes an MDOF system?
It must have multiple degrees of freedom, right?
That's right! Each movement in the structure represents a degree of freedom. Can anyone give me an example of what could be a degree of freedom?
The floors in a building can move separately!
Exactly! The floors represent individual DOFs in our MDOF model, which helps in accurately mapping out the motion of the entire structure during dynamic loading.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces Multi-Degree-of-Freedom (MDOF) systems, explaining their necessity in capturing the dynamic responses of complex structures like buildings and bridges that cannot be accurately modeled with single-degree-of-freedom (SDOF) systems. It emphasizes their importance in earthquake engineering.
Detailed
Detailed Summary
In this section, we explore the critical role of Multi-Degree-of-Freedom (MDOF) systems in the analysis of real-world structures. Unlike Single-Degree-of-Freedom (SDOF) models, which simplify structures into a single moving element, MDOF models account for the multiple interconnected components of structures, such as floors and frames. Each part can move independently in response to dynamic loads, making MDOF models necessary for realistic dynamic analysis, particularly in the field of Earthquake Engineering. When structures are subjected to dynamic loads, such as seismic excitations, a comprehensive understanding of their behavior is essential, which this chapter aims to provide by discussing the formulations, characteristics, and behaviors of MDOF systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Limitations of SDOF Models
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
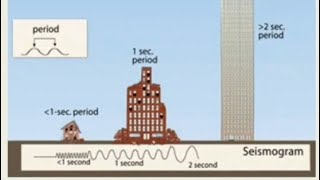
In real-world structures such as buildings, bridges, and towers, the dynamic response to ground motion or external forces cannot be accurately captured using single-degree-of-freedom (SDOF) models alone.
Detailed Explanation
Single-degree-of-freedom (SDOF) models simplify structures to one key movement point. While this can work for very simple systems, real-world structures like large buildings and bridges have many components interacting simultaneously. SDOF models fail to account for how each component—such as floors and frames—moves individually under forces like earthquakes or strong winds. Thus, relying solely on SDOF models may lead to inaccurate predictions of structural behavior during dynamic events.
Examples & Analogies
Imagine a large concert hall where each row of seats can sway individually while still being part of the whole structure. If you tried to predict how this hall responds to, say, a thunderous cheer from the audience using just a model that considers only one row, you would miss how all rows interact and contribute to the overall swaying. In contrast, a more detailed model would take into account the unique movements of every row.
Introduction to MDOF Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These structures have multiple interconnected components (floors, frames, columns, etc.), each of which can move independently in response to dynamic loading. Hence, Multi-Degree-of-Freedom (MDOF) models are essential for realistic dynamic analysis, especially in Earthquake Engineering, where lateral loads and seismic excitations act simultaneously on different points of a structure.
Detailed Explanation
Multi-degree-of-freedom (MDOF) models address the complexities of real-world structures by considering multiple independent movements of various components. Each floor or structural element is treated as a degree of freedom, allowing engineers to analyze how forces affect the whole system. In seismic engineering, this is crucial because ground motion can generate forces that impact multiple parts of a structure at the same time, leading to more accurate predictions of the building's response.
Examples & Analogies
Think of MDOF as a choreographed dance performance instead of a solo dance. Each dancer represents a component of a building; their movements may influence each other and create a cohesive performance—or in engineering terms, a structural response. Just like a choreographer needs to understand how each dancer moves relative to others to ensure the overall performance is good, engineers need MDOF models to anticipate how each part of a structure will react under dynamic loading.
Characteristics of MDOF Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
MDOF systems represent structures with more than one coordinate (degree of freedom) required to define their motion. This chapter introduces the formulation, characteristics, and behavior of MDOF systems, particularly in the context of linear elastic analysis under dynamic loading.
Detailed Explanation
MDOF systems capture the complex behavior of structures by representing them with multiple degrees of freedom. Unlike SDOF models, which can only describe motion in one direction, MDOF allows for movement in multiple directions, reflecting how components behave during dynamic events like earthquakes. The focus of the chapter is on understanding how these systems are formulated and analyzed, emphasizing linear elastic conditions, which assume that deformations are proportional to the loads applied.
Examples & Analogies
Consider a flexible suspension bridge swaying in the wind. Each part of the bridge—its towers, cables, and deck—moves in response to environmental forces. If we treated the bridge as an MDOF system, we would account for the sway of the deck as well as the tension in the cables, providing a comprehensive view of its response—similar to how different parts of an organ respond to a musician's varied play. This holistic view allows engineers to better predict behaviors under stress.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Multi-Degree-of-Freedom (MDOF) Systems: Necessary for capturing the dynamism of interconnected structures.
-
Dynamic Analysis: Essential for ensuring structures resist lateral loads under seismic conditions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A 10-story building analyzed with an MDOF model to assess earthquake response shows varying reactions across its floors.
-
Bridges undergoing dynamic load tests to evaluate responses to strong winds using MDOF principles.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
MDOF's six flows, where motion shows, each part moves, as the structure grows.
📖 Fascinating Stories
-
Imagine a multi-story building during an earthquake – each floor dances to its own rhythm, illustrating how MDOF captures their independent motions.
🧠 Other Memory Gems
-
Each floor's unique dance during a quake illustrates MDOF's true stance!
🎯 Super Acronyms
MDOF = Many Degrees; dancing blues, move differently, they cannot lose.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: MultiDegreeofFreedom Model (MDOF)
Definition:
A structural model that considers multiple independent motions of interconnected components.
-
Term: SingleDegreeofFreedom Model (SDOF)
Definition:
A simplified structural model that captures motion using a single coordinate.
-
Term: Dynamic Loading
Definition:
Forces acting on a structure that vary over time, such as those resulting from earthquakes or winds.